Comme premier exemple de série, observons le développement
décimal d'un réel strictement compris entre 0 et 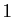 .
.
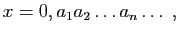
où pour tout
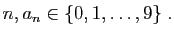
Cette écriture correspond en fait à la série de terme général
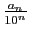 . La somme partielle
. La somme partielle 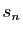 est
l'approximation décimale par défaut à
est
l'approximation décimale par défaut à 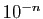 près.
Voici les 50 premières décimales de
près.
Voici les 50 premières décimales de
 .
.
Les nombres décimaux 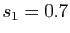 ,
, 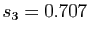 ,
,
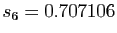 sont des sommes partielles de la série.
sont des sommes partielles de la série.
Les deux séries les plus souvent utilisées sont la série
géométrique et la série exponentielle.
Série géométrique
Le terme général d'une série géométrique est
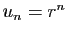 . Les sommes partielles ont une
expression explicite.
. Les sommes partielles ont une
expression explicite.
Série exponentielle
Le terme général de la série exponentielle est
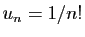 ,
où
,
où 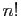 (factorielle) désigne le produit des entiers de
(factorielle) désigne le produit des entiers de 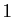 à
à
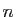 . Par convention,
. Par convention, 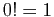 .
Les sommes partielles
.
Les sommes partielles 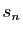 sont des rationnels mais
n'ont pas d'expression explicite.
Observons que n'importe quelle suite
sont des rationnels mais
n'ont pas d'expression explicite.
Observons que n'importe quelle suite
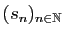 peut être
vue comme une série, de terme général
peut être
vue comme une série, de terme général
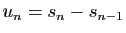 , pour
, pour
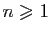 et
et 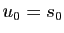 .
Dans la plupart des cas, les sommes partielles n'ont pas d'expression
explicite, et c'est souvent pour cela que l'on parle de série
plutôt que de suite.
.
Dans la plupart des cas, les sommes partielles n'ont pas d'expression
explicite, et c'est souvent pour cela que l'on parle de série
plutôt que de suite.
Définition 2
On dit que la série  converge vers
converge vers 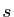 si la suite des
sommes partielles converge vers
si la suite des
sommes partielles converge vers 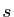 , qui est appelée somme de
la série.
, qui est appelée somme de
la série.
Dans le cas contraire, on dit que la série diverge.
Par exemple, le réel 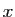 est la
limite de ses approximations décimales, et aussi la somme de la série
est la
limite de ses approximations décimales, et aussi la somme de la série
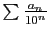 .
.
La série géométrique 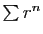 converge si et seulement si
converge si et seulement si
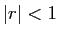 . Dans ce cas, la somme est
. Dans ce cas, la somme est
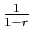 .
.
La somme de la série exponentielle est le nombre
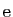 , dont le
logarithme népérien vaut
, dont le
logarithme népérien vaut 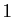 .
.
Voici un exemple de série dont les sommes partielles sont
explicitement calculables.
En effet,
donc
et
Considérons une série  et définissons la
fonction en escalier
et définissons la
fonction en escalier 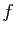 sur
sur
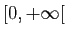 par :
par :
La somme partielle 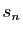 est l'intégrale de
est l'intégrale de 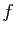 sur l'intervalle
sur l'intervalle
![$ [0,n+1]$](img45.gif) . La série
. La série  converge si et seulement si
l'intégrale
converge si et seulement si
l'intégrale
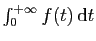 converge (voir figure
1).
converge (voir figure
1).
Réciproquement, l'intégrale d'une fonction quelconque sur
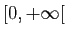 peut être vue comme la somme de la série dont le
terme général est l'intégrale sur
peut être vue comme la somme de la série dont le
terme général est l'intégrale sur 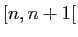 . Nous utiliserons
par la suite cette parenté entre séries et intégrales.
. Nous utiliserons
par la suite cette parenté entre séries et intégrales.
Figure 1:
Somme d'une série, vue comme l'intégrale d'une fonction
en escaliers sur
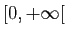 .
.
|
|
Comme la convergence d'une intégrale ne dépend que du comportement
de la fonction à l'infini, la convergence d'une série ne dépend
pas de ses premiers termes. Changer un nombre fini de termes d'une
série ajoute une même constante à toutes les sommes partielles
à partir d'un certain rang. Cela ne change pas la nature,
convergente ou divergente. Si elle est convergente,
sa somme est évidemment modifiée.
Par exemple :
Le fait de calculer la somme d'une série à partir de 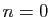 est
purement conventionnel. On peut toujours effectuer un changement
d'indice pour se ramener à une somme à partir de 0. Par
exemple :
est
purement conventionnel. On peut toujours effectuer un changement
d'indice pour se ramener à une somme à partir de 0. Par
exemple :
en posant 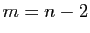 .
Le terme général d'une série convergente tend vers 0.
.
Le terme général d'une série convergente tend vers 0.
Théorème 1
Si la série  converge, alors la suite
converge, alors la suite
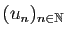 tend vers 0.
tend vers 0.
La contraposée de ce résultat est souvent utilisée : une
série dont le terme général ne tend pas vers 0 ne peut pas
converger.
Démonstration : Pour tout
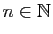 , posons
, posons
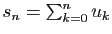 . Pour tout
. Pour tout
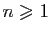 ,
,
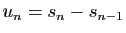 . Si
. Si  converge,
la suite
converge,
la suite
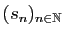 converge vers la somme
converge vers la somme 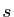 de la série. Il en
est de même de la suite
de la série. Il en
est de même de la suite
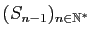 . Par linéarité de
la limite, la suite
. Par linéarité de
la limite, la suite 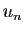 tend vers
tend vers 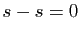 .
. Par exemple la série de terme général
Par exemple la série de terme général
diverge : même si les termes non nuls sont très rares il y en quand
même une infinité !
Le fait que le terme général tende vers 0 n'est qu'une condition
nécessaire de convergence. De nombreuses séries divergentes ont un terme
général qui tend vers 0. Par exemple, la série de terme
général
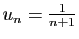 diverge. En effet :
diverge. En effet :
La suite des sommes partielles n'est pas de Cauchy, donc elle ne
converge pas.
La linéarité des limites entraîne immédiatement le théorème
suivant.
Théorème 2
Soient  et
et 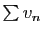 deux séries convergentes, de sommes
respectives
deux séries convergentes, de sommes
respectives 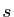 et
et 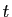 . Soient
. Soient 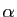 et
et 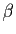 deux complexes
quelconques. Alors la série de terme général
deux complexes
quelconques. Alors la série de terme général
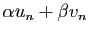 est convergente, et sa somme est
est convergente, et sa somme est
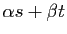 .
.
Par exemple :
Comme conséquence de la linéarité, observons que si  converge et
converge et 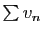 diverge, alors
diverge, alors
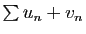 diverge. Comme
autre conséquence,
pour
diverge. Comme
autre conséquence,
pour
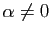 ,
,
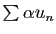 converge si et seulement si
converge si et seulement si
 converge.
converge.
Pour les séries à termes complexes la convergence équivaut à
celle des parties réelle et imaginaire.
Démonstration : Rappelons qu'une suite de nombres complexes converge si et seulement
si la suite des parties réelles et la suite des parties imaginaires
convergent. Si
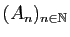 et
et
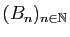 sont deux suites
de réels :
sont deux suites
de réels :
Il suffit d'appliquer ce résultat à
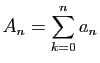
et
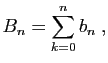
car la partie réelle d'une somme est la somme des parties réelles,
et la partie imaginaire d'une somme est la somme des parties imaginaires. Considérons par exemple la série géométrique
Considérons par exemple la série géométrique 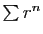 , où
, où
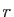 est un complexe de module
est un complexe de module 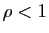 et d'argument
et d'argument 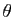 :
:
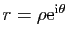 . Pour tout
. Pour tout 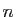 ,
,
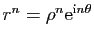 . Les
parties réelle et imaginaire de
. Les
parties réelle et imaginaire de 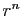 sont
sont
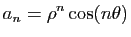
et
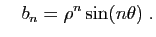
On déduit de la proposition précédente que :
Le calcul donne :
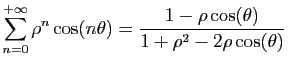
et
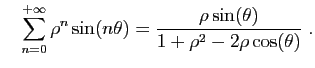
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
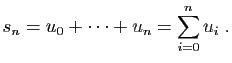
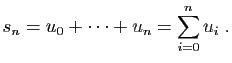
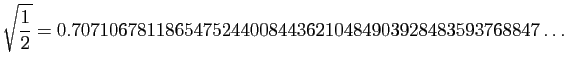
![]() . Les sommes partielles ont une
expression explicite.
. Les sommes partielles ont une
expression explicite.
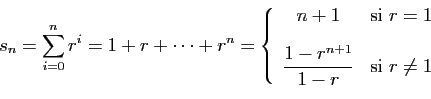
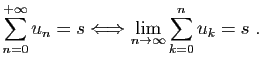
![]() converge si et seulement si
converge si et seulement si
![]() . Dans ce cas, la somme est
. Dans ce cas, la somme est
![]() .
.
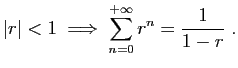
![]() , dont le
logarithme népérien vaut
, dont le
logarithme népérien vaut ![]() .
.
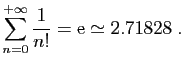
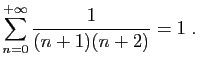
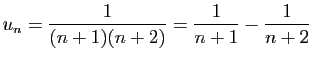
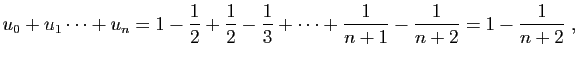
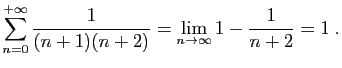
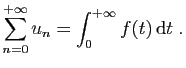
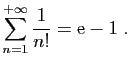
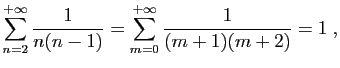
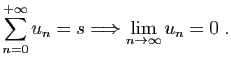
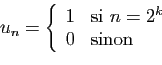
![]() diverge. En effet :
diverge. En effet :
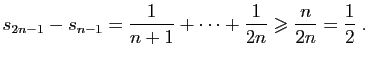
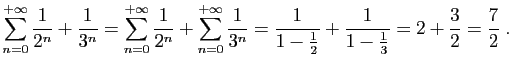
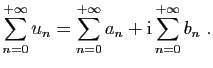
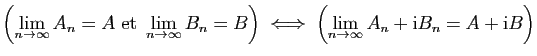
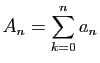 et
et 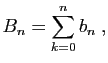
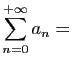 Re
Re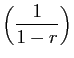 et
et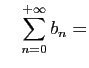 Im
Im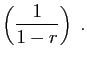
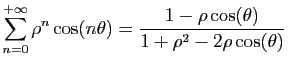 et
et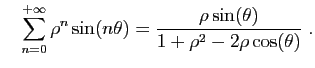
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales