La figure 3 représente un graphe : cinq sommets
numérotés de 1 à 5 et des arêtes entre eux (les arêtes ne
sont pas orientées et il n'y a pas de boucle sur un même sommet).
Figure 3:
Graphe à 5 sommets et 6 arêtes.
|
|
Imaginez que sur chaque sommet se trouve une ampoule, et un
interrupteur qui commande non seulement l'ampoule du même sommet,
mais aussi celles des sommets voisins. Par exemple appuyer sur
l'interrupteur du sommet 2 bascule l'état des ampoules 1, 2, 3 et 5, de
«éteinte» à «allumée», ou bien le contraire. La première
observation, est que l'ordre dans lequel les interrupteurs sont
actionnés, n'a pas d'influence sur le résultat.
Si tout est éteint et que vous actionnez l'interrupteur
1, les ampoules 1, 2 et 5 s'allument. Si ensuite vous
actionnez 2, les ampoules 1, 2 et 5 s'éteignent, et 3
s'allume. Le résultat est le même si l'interrupteur
2 est actionné avant le 1.
On peut donc parler de l'effet d'un ensemble d'interrupteurs,
sans considération de l'ordre dans lequel ils sont actionnés.
Si toutes les
ampoules sont éteintes, quel ensemble
d'interrupteurs faut-il actionner
pour les allumer toutes ? Ou de
manière plus condensée, comment passer de «tout noir»
à «tout blanc». De
manière assez surprenante, ce problème a toujours au moins une solution
quel que soit le graphe, et on peut le résoudre à l'aide de la
méthode du pivot de Gauss1.
Attention, les calculs ne seront pas ceux dont vous avez
l'habitude : nous abandonnons les réels pour un ensemble de nombres
beaucoup plus petit.
Pour jouer le rôle des réels, tout ensemble de nombres
doit contenir au moins les éléments neutres
pour l'addition et la multiplication : 0 et 1. Le plus petit
ensemble possible, celui des entiers modulo 2, ne contient que 0 et
1. On le note
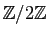 . Voici les tables d'addition et de
multiplication.
. Voici les tables d'addition et de
multiplication.
Sur l'ensemble des 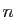 -uplets de 0 ou de 1, les
opérations de
-uplets de 0 ou de 1, les
opérations de
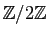 agissent composante par composante.
Par exemple pour
agissent composante par composante.
Par exemple pour 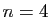 :
:
Cet ensemble, noté
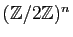 ,
est un espace vectoriel sur
,
est un espace vectoriel sur
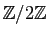 ,
tout comme
,
tout comme
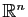 est un espace
vectoriel sur
est un espace
vectoriel sur
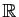 . La méthode de
résolution des systèmes linéaires dans
. La méthode de
résolution des systèmes linéaires dans
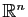 , reste valable dans
, reste valable dans
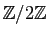 , en n'oubliant pas que
, en n'oubliant pas que 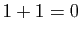 .
Etant donné le problème «tout blanc - tout noir» sur un
graphe à
.
Etant donné le problème «tout blanc - tout noir» sur un
graphe à 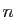 sommets, nous allons lui associer un système
linéaire de
sommets, nous allons lui associer un système
linéaire de 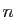 équations à
équations à 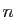 inconnues.
inconnues.
Il faut comprendre un 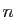 -uplet
-uplet
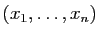 de 0 et de 1
comme une description de l'ensemble des interrupteurs qui seront
actionnés :
de 0 et de 1
comme une description de l'ensemble des interrupteurs qui seront
actionnés : 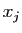 vaut 1 si l'interrupteur
vaut 1 si l'interrupteur 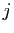 est actionné,
0 sinon. Les coefficients
est actionné,
0 sinon. Les coefficients 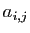 décrivent l'effet des
interrupteurs sur les ampoules :
décrivent l'effet des
interrupteurs sur les ampoules : 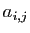 vaut 1 si l'interrupteur
vaut 1 si l'interrupteur
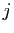 actionne l'ampoule
actionne l'ampoule 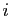 , 0 sinon. Le premier membre de la ligne
, 0 sinon. Le premier membre de la ligne
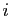 décrit l'effet de la combinaison d'interrupteurs
décrit l'effet de la combinaison d'interrupteurs
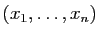 sur l'ampoule
sur l'ampoule 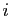 :
:
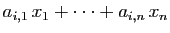 vaut 1 si l'ampoule
vaut 1 si l'ampoule 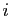 est
finalement allumée, 0 si elle est éteinte. Tous les termes du
second membre sont égaux à 1, car on souhaite que toutes les
ampoules soient allumées à la fin.
est
finalement allumée, 0 si elle est éteinte. Tous les termes du
second membre sont égaux à 1, car on souhaite que toutes les
ampoules soient allumées à la fin.
Voici le système correspondant à la figure
3.
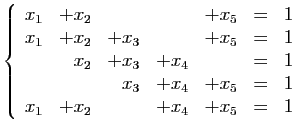 |
(7) |
Vous pouvez vérifier que
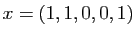 est solution
(dans
est solution
(dans
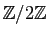 ) : actionner les interrupteurs 1, 2 et 5 allume
bien toutes les ampoules dans la figure 3.
) : actionner les interrupteurs 1, 2 et 5 allume
bien toutes les ampoules dans la figure 3.
Si le graphe est trop compliqué pour deviner la solution, comment la
calculer ? Par la méthode du pivot de Gauss bien sûr ! Ce qui a
été exposé pour les matrices à coefficients réels, vaut pour
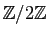 .
Si on applique la méthode du pivot de Gauss au système (7),
on vérifie qu'il est de rang 5, donc
.
Si on applique la méthode du pivot de Gauss au système (7),
on vérifie qu'il est de rang 5, donc
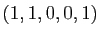 est l'unique
solution. Dans ce cas particulier, le système a une
solution unique pour tout second membre.
Donc quelle que soit la configuration d'ampoules allumées et
éteintes que l'on souhaite atteindre, il y a un
ensemble d'interrupteurs et un seul que l'on doit actionner pour
atteindre la configuration souhaitée.
est l'unique
solution. Dans ce cas particulier, le système a une
solution unique pour tout second membre.
Donc quelle que soit la configuration d'ampoules allumées et
éteintes que l'on souhaite atteindre, il y a un
ensemble d'interrupteurs et un seul que l'on doit actionner pour
atteindre la configuration souhaitée.
Ce n'est pas toujours le cas. Le graphe complet à 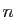 sommets est
tel que deux sommets quelconques sont toujours reliés par une
arête. Sur un graphe complet, basculer un interrupteur quelconque
allume ou éteint toutes les ampoules à la fois. Si on commence au
début par toutes les ampoules éteintes, la seule autre
configuration que l'on puisse atteindre est celle où tout est
allumé. Dans ce cas, tous les coefficients
sommets est
tel que deux sommets quelconques sont toujours reliés par une
arête. Sur un graphe complet, basculer un interrupteur quelconque
allume ou éteint toutes les ampoules à la fois. Si on commence au
début par toutes les ampoules éteintes, la seule autre
configuration que l'on puisse atteindre est celle où tout est
allumé. Dans ce cas, tous les coefficients 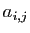 du système
sont égaux à 1, son rang est 1,
et le système n'a de solution que si
tous les coefficients du second membre sont égaux.
du système
sont égaux à 1, son rang est 1,
et le système n'a de solution que si
tous les coefficients du second membre sont égaux.
Le miracle est que si tous les coefficients du second membre sont
égaux à 1, le système a toujours au moins
une solution : quel que soit le graphe, il y a toujours un ensemble
d'interrupteurs à actionner pour allumer toutes les ampoules.
Théorème 5
Pour tout graphe à 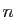 sommets, le système
sommets, le système 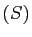 a au moins une
solution.
a au moins une
solution.
Démonstration : Appliquons la méthode du pivot de Gauss au système 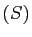 . On
le transforme en prenant des combinaisons linéaires des lignes,
jusqu'à le mettre sous forme échelonnée. Si le rang du système
est
. On
le transforme en prenant des combinaisons linéaires des lignes,
jusqu'à le mettre sous forme échelonnée. Si le rang du système
est 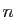 , il n'y aura pas d'équation de compatibilité : le
système se résout, et on trouve une solution unique. Mais si le
rang est inférieur à
, il n'y aura pas d'équation de compatibilité : le
système se résout, et on trouve une solution unique. Mais si le
rang est inférieur à 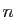 , la méthode du pivot de Gauss fait
apparaître une combinaison linéaire des équations dont le
premier membre est nul.
Or nous sommes dans
, la méthode du pivot de Gauss fait
apparaître une combinaison linéaire des équations dont le
premier membre est nul.
Or nous sommes dans
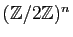 : les coefficients d'une
combinaison linéaire ne peuvent être que 0 ou 1. Donc une
combinaison linéaire est forcément une somme. Que se passe-t-il
quand une somme de lignes, disons
: les coefficients d'une
combinaison linéaire ne peuvent être que 0 ou 1. Donc une
combinaison linéaire est forcément une somme. Que se passe-t-il
quand une somme de lignes, disons
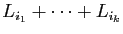 a un premier membre nul ? Cela implique en particulier que chacun des sommets
a un premier membre nul ? Cela implique en particulier que chacun des sommets
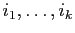 a un nombre impair de voisins parmi les autres
sommets du même ensemble
a un nombre impair de voisins parmi les autres
sommets du même ensemble
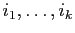 .
Si on restreint le graphe à ces sommets,
on obtient un sous-graphe, tel que le nombre de voisins de chaque
sommet est impair. Or dans un graphe ayant un nombre impair de
sommets, il y a toujours un sommet dont le nombre de voisins est pair
(ce n'est pas facile à démontrer : réflechissez !). Si tous les
sommets parmi
.
Si on restreint le graphe à ces sommets,
on obtient un sous-graphe, tel que le nombre de voisins de chaque
sommet est impair. Or dans un graphe ayant un nombre impair de
sommets, il y a toujours un sommet dont le nombre de voisins est pair
(ce n'est pas facile à démontrer : réflechissez !). Si tous les
sommets parmi
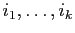 ont un nombre impair de voisins, alors
ont un nombre impair de voisins, alors
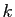 est pair. Donc
si
est pair. Donc
si
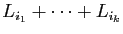 a un premier membre nul,
alors nécessairement
a un premier membre nul,
alors nécessairement 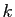 est un
entier pair. Pour appliquer la méthode du pivot de Gauss, on doit
effectuer les mêmes transformations à la fois sur le premier membre
et sur le second. Or le second ne contient que des 1. La somme dans
est un
entier pair. Pour appliquer la méthode du pivot de Gauss, on doit
effectuer les mêmes transformations à la fois sur le premier membre
et sur le second. Or le second ne contient que des 1. La somme dans
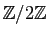 d'un nombre pair de 1 donne 0. Ceci entraîne que si la
forme échelonnée contient une équation dont le premier
membre est nul, alors le second membre de cette même équation est
nul également. Donc le système
a une solution.
d'un nombre pair de 1 donne 0. Ceci entraîne que si la
forme échelonnée contient une équation dont le premier
membre est nul, alors le second membre de cette même équation est
nul également. Donc le système
a une solution.
Le théorème 2 entraîne que l'ensemble des
solutions est en bijection avec un sous-espace vectoriel de
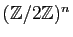 . Un sous-espace vectoriel de dimension
. Un sous-espace vectoriel de dimension 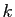 dans
dans
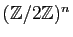 a
a 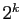 éléments.
Le nombre de solutions est donc nécessairement une
puissance de 2. Pour le graphe de la figure 4, vous
pouvez calculer les solutions par la méthode du pivot de Gauss, et
vérifier qu'il y en a 2.
éléments.
Le nombre de solutions est donc nécessairement une
puissance de 2. Pour le graphe de la figure 4, vous
pouvez calculer les solutions par la méthode du pivot de Gauss, et
vérifier qu'il y en a 2.
Figure 4:
Graphe à 6 sommets et 9 arêtes.
|
|
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![\includegraphics[width=5cm]{graphe5}](img267.gif)
![]() . Voici les tables d'addition et de
multiplication.
. Voici les tables d'addition et de
multiplication.
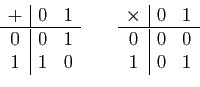
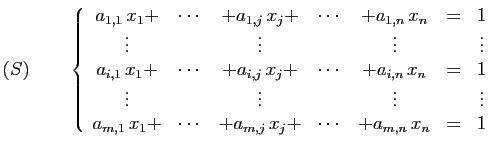
![]() .
Si on applique la méthode du pivot de Gauss au système (7),
on vérifie qu'il est de rang 5, donc
.
Si on applique la méthode du pivot de Gauss au système (7),
on vérifie qu'il est de rang 5, donc
![]() est l'unique
solution. Dans ce cas particulier, le système a une
solution unique pour tout second membre.
Donc quelle que soit la configuration d'ampoules allumées et
éteintes que l'on souhaite atteindre, il y a un
ensemble d'interrupteurs et un seul que l'on doit actionner pour
atteindre la configuration souhaitée.
est l'unique
solution. Dans ce cas particulier, le système a une
solution unique pour tout second membre.
Donc quelle que soit la configuration d'ampoules allumées et
éteintes que l'on souhaite atteindre, il y a un
ensemble d'interrupteurs et un seul que l'on doit actionner pour
atteindre la configuration souhaitée.
![]() sommets est
tel que deux sommets quelconques sont toujours reliés par une
arête. Sur un graphe complet, basculer un interrupteur quelconque
allume ou éteint toutes les ampoules à la fois. Si on commence au
début par toutes les ampoules éteintes, la seule autre
configuration que l'on puisse atteindre est celle où tout est
allumé. Dans ce cas, tous les coefficients
sommets est
tel que deux sommets quelconques sont toujours reliés par une
arête. Sur un graphe complet, basculer un interrupteur quelconque
allume ou éteint toutes les ampoules à la fois. Si on commence au
début par toutes les ampoules éteintes, la seule autre
configuration que l'on puisse atteindre est celle où tout est
allumé. Dans ce cas, tous les coefficients ![]() du système
sont égaux à 1, son rang est 1,
et le système n'a de solution que si
tous les coefficients du second membre sont égaux.
du système
sont égaux à 1, son rang est 1,
et le système n'a de solution que si
tous les coefficients du second membre sont égaux.
![]() . Un sous-espace vectoriel de dimension
. Un sous-espace vectoriel de dimension ![]() dans
dans
![]() a
a ![]() éléments.
Le nombre de solutions est donc nécessairement une
puissance de 2. Pour le graphe de la figure 4, vous
pouvez calculer les solutions par la méthode du pivot de Gauss, et
vérifier qu'il y en a 2.
éléments.
Le nombre de solutions est donc nécessairement une
puissance de 2. Pour le graphe de la figure 4, vous
pouvez calculer les solutions par la méthode du pivot de Gauss, et
vérifier qu'il y en a 2.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales