Ensemble des solutions

Nous nous limitons dans ce chapitre au cas réel, mais ce qui suit reste valable sur $\mathbb{C}$ .

Considérons un système de équations à inconnues.

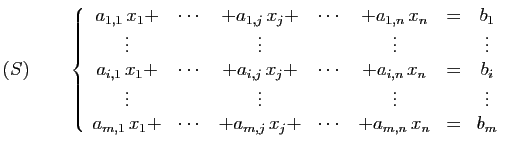
$\displaystyle (S)\qquad \left\{\begin{array}{ccccccc} a_{1,1} x_1+&\cdots&+a_{... ...m,1} x_1+&\cdots&+a_{m,j} x_j+&\cdots&+a_{m,n} x_n&=&b_m \end{array}\right.$

Les coefficients $a_{i,j}$ et

sont des réels donnés. Les variables

sont les inconnues. Il faut comprendre

comme la conjonction («et») de

assertions portant sur les variables $(x_1,\ldots,x_n)$ . Une solution est un

-uplet de réels qui vérifie chacune des

équations. L'ensemble des solutions est un sous-ensemble de $\mathbb{R}^n$ . Deux systèmes à

inconnues sont équivalents si et seulement si leurs ensembles de solutions sont les mêmes.

Par convention, on regroupe les termes contenant les inconnues à gauche de l'égalité, les termes constants à droite. La partie gauche s'appelle le premier membre, le -uplet des constantes à droite de l'égalité est le second membre. On dit d'un système qu'il est homogène si tous les termes du second membre sont nuls. À un système , on associe le système homogène obtenu en conservant le premier membre de et en annulant le second membre.

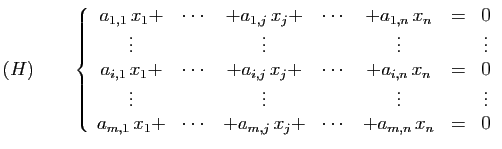
$\displaystyle (H)\qquad \left\{\begin{array}{ccccccc} a_{1,1} x_1+&\cdots&+a_{... ..._{m,1} x_1+&\cdots&+a_{m,j} x_j+&\cdots&+a_{m,n} x_n&=&0 \end{array}\right.$

Nous commençons par l'ensemble des solutions d'un système homogème.

Théorème 1 Soit un système homogène de équations à inconnues. L'ensemble des solutions de est un sous-espace vectoriel de $\mathbb{R}^n$ .

Démonstration : Observons que le

-uplet $(0,\ldots,0)$ (vecteur nul de $\mathbb{R}^n$ ) est solution. L'ensemble des solutions de

n'est donc jamais vide.

Pour montrer qu'un ensemble non vide est un sous-espace vectoriel de $\mathbb{R}^n$ , il suffit de vérifier qu'il est stable par combinaison linéaire, c'est-à-dire que si deux éléments appartiennent à l'ensemble, toutes leurs combinaisons linéaires restent dans le même ensemble. Soient $x=(x_1,\ldots,x_n)$ et $y=(y_1,\ldots,y_n)$ deux solutions de , $\lambda$ et $\mu$ deux réels quelconques. Nous devons vérifier que $\lambda x+\mu y$ est solution de . Considérons la -ième équation, vérifiée à la fois par et .

$\displaystyle a_{i,1} x_1+\ldots+a_{i,n} x_n=0$ et $\displaystyle \quad a_{i,1} y_1+\ldots+a_{i,n} y_n=0\;.$

En multipliant la première par $\lambda$ , la seconde par $\mu$ et en ajoutant les deux, on obtient :

$\displaystyle \lambda(a_{i,1} x_1+\ldots+a_{i,n} x_n) +\mu(a_{i,1} x_1+\ldots+a_{i,n} x_n)=0\;,$

soit,

$\displaystyle a_{i,1} (\lambda x_1+\mu y_1)+\ldots+a_{i,n} (\lambda x_n+\mu y_n)=0\;.$

-uplet $(\lambda x_1+\mu y_1,\ldots,\lambda x_n+\mu y_n)$ est donc solution de

. $\square$

Tout sous-espace vectoriel de $\mathbb{R}^n$ est de dimension finie, au plus égale à . Soit l'espace vectoriel des solutions du système homogène . Il se peut que soit de dimension 0, si $(0,\ldots,0)$ est la seule solution de . Nous verrons plus loin que la dimension de est au moins égale à : un système homogène ayant moins d'équations que d'inconnues a une infinité de solutions. Soit la dimension de , et $s_1,\ldots,s_k$ solutions particulières, formant une base de . Toute solution de s'écrit de façon unique comme combinaison linéaire de $s_1,\ldots,s_k$ .

$\displaystyle E = \{ \lambda_1s_1+\cdots+\lambda_k s_k ,\;\lambda_1,\ldots,\lambda_k\in\mathbb{R} \}\;.$

(1)

Théorème 2 Soit un système linéaire et le système homogène associé. Notons ${\cal S}$ l'ensemble des solutions de et l'espace vectoriel des solutions de . Alors,

$\bullet$: soit ${\cal S}$ est vide,
$\bullet$: soit ${\cal S}$ est un espace affine de direction .

Démonstration : Supposons ${\cal S}$ non vide : soit $s_0=(x_1^{(0)},\ldots,x_n^{(0)})$ une solution particulière de

. Nous allons démontrer que toute solution de

est la somme de

et d'une solution de

. Soit $s=(x_1,\ldots,x_n)$ une solution quelconque de

. Pour tout $i=1,\ldots,m$ , les deux solutions satisfont la

-ième équation.

$\displaystyle a_{i,1} x_1^{(0)}+\ldots+a_{i,n} x_n^{(0)}=b_i$ et $\displaystyle \quad a_{i,1} x_1+\ldots+a_{i,n} x_n=b_i\;.$

Si on retranche la première équation de la seconde, on obtient :

$\displaystyle a_{i,1} (x_1-x_1^{(0)})+\ldots+a_{i,n} (x_n-x_n^{(0)})=0\;.$

Par conséquent, le

-uplet

est solution du système homogène associé

Réciproquement, on vérifie de la même façon que tout -uplet somme de et d'une solution de est solution de . $\square$

En joignant le théorème 2 et (1), on peut écrire l'ensemble des solutions de comme suit.

$\displaystyle {\cal S} = \{ s_0+\lambda_1s_1+\cdots+\lambda_k s_k ,\;\lambda_1,\ldots,\lambda_k\in\mathbb{R} \}\;.$

(2)

Vous pouvez retenir ce résultat ainsi :

La solution générale d'un système linéaire est la somme
d'une solution particulière
et de la solution générale du système homogène associé.

On retrouve ce même principe dans des problèmes très différents : équations de récurrence, équations différentielles, etc.

Le reste de ce chapitre est consacré à la méthode du pivot de Gauss qui permet de calculer explicitement des uplets $s_0,s_1,\ldots,s_k$ , tels que soit une solution particulière de et $(s_1,\ldots,s_k)$ soit une base de l'espace vectoriel des solutions de .