Quand un système linéaire de 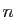 équations à
équations à 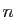 inconnues est
de rang
inconnues est
de rang 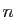 , il a une solution unique. Il existe une formule
explicite qui relie la solution
, il a une solution unique. Il existe une formule
explicite qui relie la solution
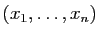 aux
coefficients. Elle est connue, au moins
pour les faibles valeurs de
aux
coefficients. Elle est connue, au moins
pour les faibles valeurs de 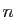 , depuis très longtemps, même si
elle est attribuée traditionnellement au mathématicien genevois
Gabriel Cramer (1704-1752).
Commençons par le cas
, depuis très longtemps, même si
elle est attribuée traditionnellement au mathématicien genevois
Gabriel Cramer (1704-1752).
Commençons par le cas 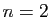 .
.
Ce système a une solution unique si et seulement si son
déterminant est non nul.
Si c'est le cas, les coordonnées de la solution s'écrivent comme
des rapports de déterminants.
Une formule analogue permet de calculer la solution d'un système
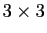 .
.
Ce système a une solution unique si et seulement si son
déterminant est non nul.
Si c'est le cas les coordonnées de la solution s'écrivent encore
comme des rapports de déterminants.
La notion de déterminant s'étend à des tableaux carrés de
nombres 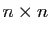 pour
pour 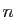 quelconque. On peut en donner la définition
récursive suivante.
quelconque. On peut en donner la définition
récursive suivante.
Vous pouvez vérifier que l'application de cette définition à un
déterminant 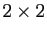 ou
ou 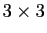 donne bien le calcul que vous savez
effectuer.
Les formules de Cramer
expriment les coordonnées de la solution d'un système de
donne bien le calcul que vous savez
effectuer.
Les formules de Cramer
expriment les coordonnées de la solution d'un système de 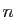 équations
à
équations
à 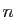 inconnues comme des rapports de déterminants.
inconnues comme des rapports de déterminants.
Le déterminant de ce système est celui du tableau des
coefficients du premier membre.
Pour séduisantes qu'elles soient, les formules de Cramer sont parfaitement
inefficaces. Le problème vient du calcul du déterminant. Si on
applique la définition récursive 2, elle
implique 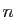 calculs de déterminants de taille
calculs de déterminants de taille
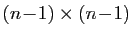 ,
suivis de
,
suivis de 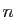 multiplications et
multiplications et 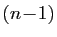 additions. Pour chacun des
déterminants de taille
additions. Pour chacun des
déterminants de taille
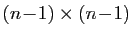 , il faudra recommencer
avec
, il faudra recommencer
avec 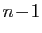 déterminants de taille
déterminants de taille
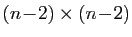 . Au total, si
on programme avec un algorithme récursif la définition
2, le calcul d'un déterminant
. Au total, si
on programme avec un algorithme récursif la définition
2, le calcul d'un déterminant 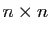 prendra
de l'ordre de
prendra
de l'ordre de 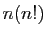 opérations.
Il se trouve que le bon moyen algorithmique de calculer un
déterminant est ... la méthode du pivot de Gauss. On montre en
effet qu'un déterminant n'est pas modifié si on ajoute à une
ligne une combinaison linéaire des autres. Il est changé en son
opposé si deux lignes ou deux colonnes sont permutées. Si on
applique la méthode du pivot de Gauss au système
opérations.
Il se trouve que le bon moyen algorithmique de calculer un
déterminant est ... la méthode du pivot de Gauss. On montre en
effet qu'un déterminant n'est pas modifié si on ajoute à une
ligne une combinaison linéaire des autres. Il est changé en son
opposé si deux lignes ou deux colonnes sont permutées. Si on
applique la méthode du pivot de Gauss au système 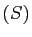 , on arrive
à un système échelonné
, on arrive
à un système échelonné 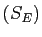 . Le déterminant de
. Le déterminant de 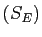 est celui d'un tableau de nombres triangulaire : ses
coefficients au-dessous de la diagonale sont nuls. Le déterminant
de
est celui d'un tableau de nombres triangulaire : ses
coefficients au-dessous de la diagonale sont nuls. Le déterminant
de 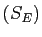 , qui est égal ou opposé à celui de
, qui est égal ou opposé à celui de 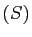 , est tout
simplement le produit des pivots. Le nombre d'opérations pour calculer un
déterminant
, est tout
simplement le produit des pivots. Le nombre d'opérations pour calculer un
déterminant 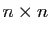 par la méthode du pivot de Gauss est de
l'ordre de
par la méthode du pivot de Gauss est de
l'ordre de
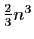 , soit très inférieur à ce que
requiert la définition 2.
, soit très inférieur à ce que
requiert la définition 2.
Donc pour utiliser les formules de Cramer, il faudrait appliquer la
méthode du pivot de Gauss à 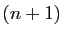 systèmes, avant d'effectuer
les quotients des déterminants obtenus : mieux vaut ne l'appliquer
qu'à un seul !
systèmes, avant d'effectuer
les quotients des déterminants obtenus : mieux vaut ne l'appliquer
qu'à un seul !
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
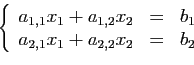
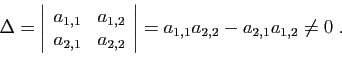
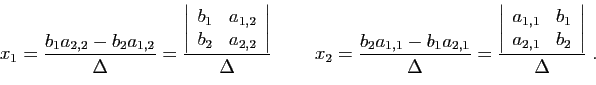
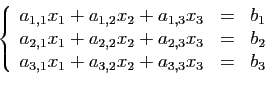
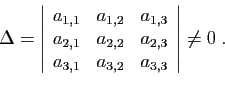
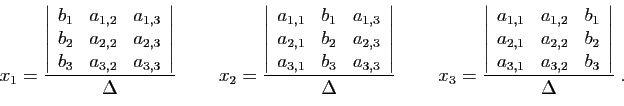
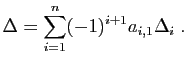
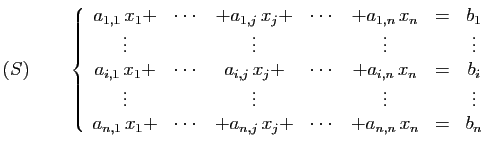
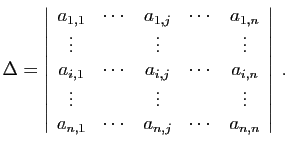
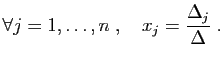
![]() systèmes, avant d'effectuer
les quotients des déterminants obtenus : mieux vaut ne l'appliquer
qu'à un seul !
systèmes, avant d'effectuer
les quotients des déterminants obtenus : mieux vaut ne l'appliquer
qu'à un seul !
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales