Nous allons passer en revue quelques développements
classiques, que vous connaissez probablement déjà depuis le
chapitre sur les développements limités. Nous ne nous
préoccuperons pas toujours de la détermination du rayon de convergence,
que nous laissons au lecteur à titre d'exercice : il vaut 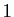 pour
pour
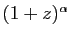 et ses avatars,
et ses avatars, 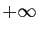 pour
pour 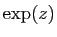 et ses
avatars, etc.
Le calcul des dérivées
successives en 0 est rarement le moyen le plus simple de calculer un
développement en série entière. Une exception notable est
et ses
avatars, etc.
Le calcul des dérivées
successives en 0 est rarement le moyen le plus simple de calculer un
développement en série entière. Une exception notable est
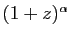 , où
, où 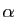 est un réel quelconque. Si
est un réel quelconque. Si
 , les dérivées successives de
, les dérivées successives de  sont :
sont :
On obtient donc :
Dans le cas particulier où  est un entier positif, les
dérivées successives sont nulles à partir d'un certain rang,
puisque
est un entier positif, les
dérivées successives sont nulles à partir d'un certain rang,
puisque
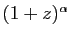 est un polynôme. Dans ce cas, le
développement se réduit à la formule du binôme de Newton que
vous connaissez déjà. Les
autres cas particuliers fréquemment rencontrés sont
est un polynôme. Dans ce cas, le
développement se réduit à la formule du binôme de Newton que
vous connaissez déjà. Les
autres cas particuliers fréquemment rencontrés sont
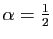 ,
,
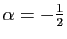 et ceux où
et ceux où 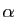 est un entier
négatif.
est un entier
négatif.
Du développement de
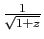 , on déduit celui de
, on déduit celui de
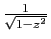 , en remplaçant
, en remplaçant 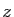 par
par 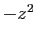 .
La primitive de
.
La primitive de
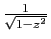 nulle en 0 est
nulle en 0 est
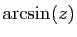 .
.
Les principales techniques de calcul de
développement en série entière sont d'une part les combinaisons
linéaires et les changements de variables, d'autre part la
dérivation et l'intégration. Par exemple, à partir de la
série exponentielle, on obtient les développements de
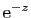 ,
,
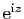 ,
,
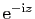 , puis ceux des sinus et cosinus usuels et
hyperboliques grâce aux formules d'Euler, que nous rappelons.
, puis ceux des sinus et cosinus usuels et
hyperboliques grâce aux formules d'Euler, que nous rappelons.
Tous les développements en série des fractions
rationnelles et de leurs primitives peuvent s'obtenir à partir de la
série géométrique.
Considérons une fraction rationnelle du type 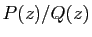 , où
, où 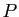 et
et 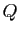 sont deux polynômes, supposés
premiers entre eux (fraction irréductible). Les pôles de la
fraction sont les complexes qui annulent le dénominateur.
sont deux polynômes, supposés
premiers entre eux (fraction irréductible). Les pôles de la
fraction sont les complexes qui annulent le dénominateur.
Par exemple, bien qu'elle soit définie sur tout
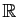 ,
la fraction
,
la fraction
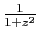 n'est développable en
série entière que sur
n'est développable en
série entière que sur
![$ ]\!-\!1,1 [$](img190.gif) , car ses pôles sont
, car ses pôles sont
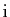 et
et
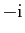 .
Démonstration : Donner cette démonstration nous permettra de détailler une
technique générale de calcul du développement en série des fractions
rationnelles. Observons tout d'abord que si 0 est un pôle, alors la
fraction n'est pas définie en 0, elle ne peut donc pas être
développable sur un intervalle contenant 0.
.
Démonstration : Donner cette démonstration nous permettra de détailler une
technique générale de calcul du développement en série des fractions
rationnelles. Observons tout d'abord que si 0 est un pôle, alors la
fraction n'est pas définie en 0, elle ne peut donc pas être
développable sur un intervalle contenant 0.
La première étape consiste à décomposer la fraction en
éléments simples. La partie entière est un polynôme, qui
modifiera éventuellement les premiers termes de la série.
Pour les besoins de la démonstration, nous
utiliserons la décomposition dans
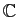 , qui ne contient que des
éléments simples du type
, qui ne contient que des
éléments simples du type
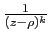 , où
, où 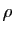 désigne un pôle. On écrit alors :
désigne un pôle. On écrit alors :
Or
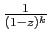 est développable en série entière sur
est développable en série entière sur
![$ ]\!-\!1,1 [$](img190.gif) .
.
En remplaçant 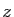 par
par
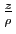 , on obtient pour tout
, on obtient pour tout
![$ z\in]\!-\!\vert\rho\vert,\vert\rho\vert [$](img282.gif) ,
,
Comme la fraction rationnelle est combinaison linéaire
d'éléments simples, le résultat de la proposition se déduit du
théorème 3. Voici un exemple détaillé.
Voici un exemple détaillé.
Cette fraction a deux pôles, 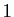 et
et 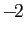 . Elle est développable
en série entière sur
. Elle est développable
en série entière sur
![$ ]\!-\!1,1 [$](img190.gif) . Nous devons calculer
séparément les développements des éléments simples.
. Nous devons calculer
séparément les développements des éléments simples.
En ajoutant les deux séries, et en tenant compte de la partie
entière pour les deux premiers termes, on obtient :
Evidemment on pouvait prévoir que les premiers termes seraient nuls
et développer
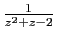 , puis décaler la série obtenue
en remplaçant
, puis décaler la série obtenue
en remplaçant 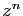 par
par 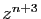 . Le lecteur vérifiera que le
résultat est bien le même.
. Le lecteur vérifiera que le
résultat est bien le même.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
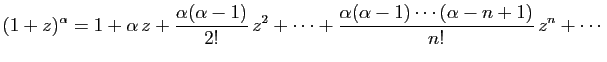
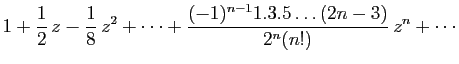
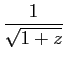
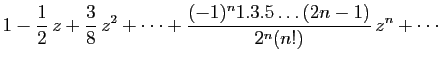
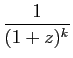
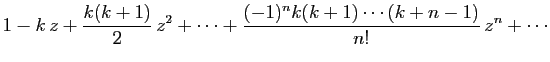
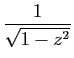
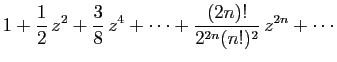
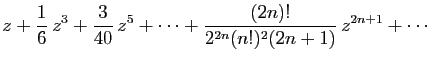
![]() ,
,
![]() ,
,
![]() , puis ceux des sinus et cosinus usuels et
hyperboliques grâce aux formules d'Euler, que nous rappelons.
, puis ceux des sinus et cosinus usuels et
hyperboliques grâce aux formules d'Euler, que nous rappelons.
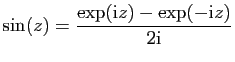
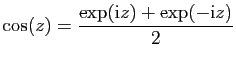
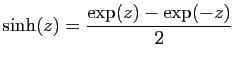
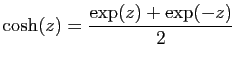
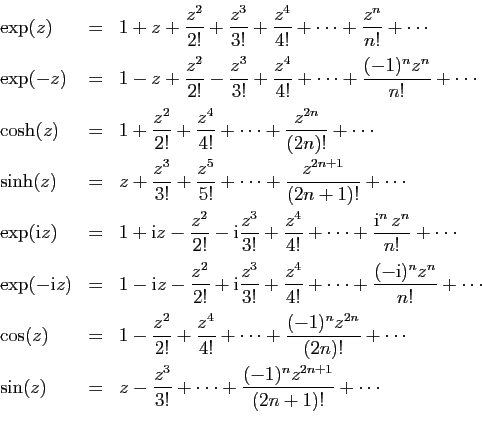
![]() , qui ne contient que des
éléments simples du type
, qui ne contient que des
éléments simples du type
![]() , où
, où ![]() désigne un pôle. On écrit alors :
désigne un pôle. On écrit alors :
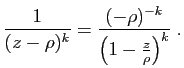
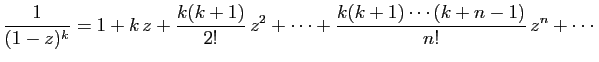
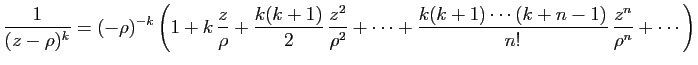
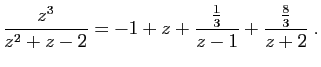
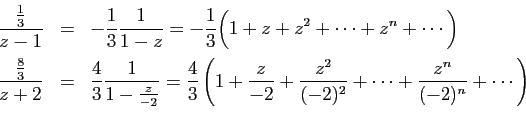
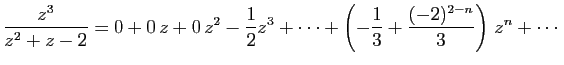
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales