Les résultats de cette section ont de nombreuses
conséquences pratiques sur les calculs de sommes de séries
entières.
Nous examinons le comportement des séries par rapport aux
opérations habituelles (combinaisons linéaires et produit).
Démonstration : La linéarité découle immédiatement des résultats analogues
sur les suites et séries numériques. Concernant le produit, nous
commençons par la convergence. Soit 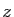 tel que
tel que
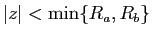 .
.
Puisque 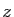 est inférieur à la fois à
est inférieur à la fois à 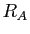 et
et 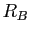 , les
deux séries
, les
deux séries
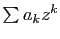 et
et
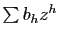 sont absolument
convergentes. Les inégalités ci-dessus montrent que les sommes
partielles de la série de terme général
sont absolument
convergentes. Les inégalités ci-dessus montrent que les sommes
partielles de la série de terme général
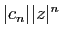 sont
bornées. Comme ces sommes partielles sont croissantes et majorées
elle convergent. Donc
sont
bornées. Comme ces sommes partielles sont croissantes et majorées
elle convergent. Donc
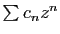 est absolument convergente.
De plus :
est absolument convergente.
De plus :
Comme la série de terme général
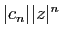 est absolument
convergente, son reste à l'ordre
est absolument
convergente, son reste à l'ordre 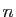 tend vers 0, d'où le résultat.
tend vers 0, d'où le résultat. Le théorème 3 affirme que les
combinaisons linéaires et le produit
de deux séries entières convergent au moins si ces deux séries
convergent. Mais il peut se faire que le rayon de convergence de la
série somme ou de la série produit soient strictement supérieurs
à
Le théorème 3 affirme que les
combinaisons linéaires et le produit
de deux séries entières convergent au moins si ces deux séries
convergent. Mais il peut se faire que le rayon de convergence de la
série somme ou de la série produit soient strictement supérieurs
à
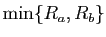 . Par exemple, les deux séries
. Par exemple, les deux séries
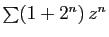 et
et
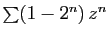 ont pour rayon de convergence
ont pour rayon de convergence
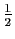 . Leur
somme
. Leur
somme
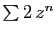 a pour rayon de convergence
a pour rayon de convergence 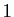 . La série
. La série 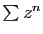 a pour rayon de convergence
a pour rayon de convergence 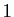 , le polynôme
, le polynôme 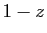 est une
série entière particulière, de rayon de convergence infini. Leur
produit est la constante
est une
série entière particulière, de rayon de convergence infini. Leur
produit est la constante 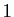 , de rayon de convergence infini.
Considérons maintenant les deux séries
, de rayon de convergence infini.
Considérons maintenant les deux séries 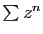 , de rayon de
convergence
, de rayon de
convergence 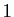 et de somme
et de somme
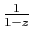 , et
, et
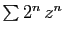 , de
rayon de convergence
, de
rayon de convergence
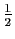 , et de somme
, et de somme
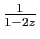 . Comme conséquence du théorème
3, pour tout
. Comme conséquence du théorème
3, pour tout 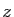 ,
, 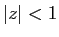 , on a :
, on a :
Aussi :
Les deux séries sont égales, comme on pouvait s'y attendre.
Voici une autre application de la linéarité. Considérons la
série
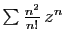 , de rayon de convergence infini.
On peut écrire :
, de rayon de convergence infini.
On peut écrire :
La même technique s'applique pour sommer toutes les séries
entières du type
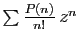 , si
, si 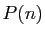 est un
polynôme en
est un
polynôme en 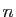 . On commence par exprimer
. On commence par exprimer 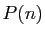 comme combinaison
linéaire de
comme combinaison
linéaire de 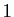 ,
, 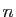 ,
, 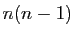 , ... et on se ramène ensuite à la
série exponentielle par des changements d'indice.
, ... et on se ramène ensuite à la
série exponentielle par des changements d'indice.
Comme nouvelle application du théorème 3,
nous allons vérifier la propriété fondamentale de
l'exponentielle.
Proposition 2
Si pour tout
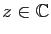 , on définit
, on définit 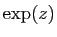 comme la somme de la
série
comme la somme de la
série
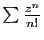 , alors :
, alors :
Démonstration : On peut voir 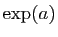 comme la valeur en
comme la valeur en 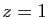 de la série
de la série
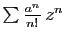 , et
, et 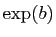 comme la valeur en
comme la valeur en
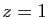 de la série
de la série
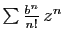 . D'après le
théorème 3, le produit de ces deux
séries est la série
. D'après le
théorème 3, le produit de ces deux
séries est la série
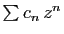 , avec :
, avec :
d'après la formule du binôme de Newton.
La série
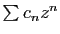 a donc pour somme
a donc pour somme
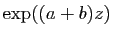 , et sa
valeur en
, et sa
valeur en 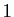 est
est 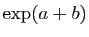 .
. Dans la proposition précédente, nous avons remplacé
Dans la proposition précédente, nous avons remplacé 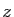 par
par 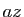 et
et 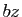 dans la série exponentielle. Remplacer la variable
dans la série exponentielle. Remplacer la variable 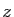 par
une fonction de celle-ci est une opération que l'on utilise
fréquemment. En voici deux exemples. Pour tout
par
une fonction de celle-ci est une opération que l'on utilise
fréquemment. En voici deux exemples. Pour tout 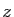 tel que
tel que 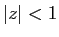 ,
on a :
,
on a :
Remplaçons 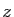 par
par 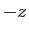 :
:
Remplaçons 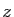 par
par 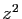 :
:
On aurait pu obtenir ce résultat de deux autres façons en
utilisant le théorème 3, puisque :
Le lecteur vérifiera que les trois méthodes conduisent au même
résultat.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
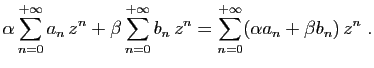
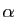 et
et 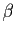 .
.
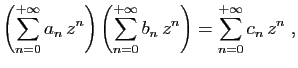
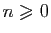 ,
,
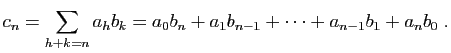
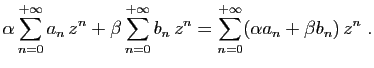
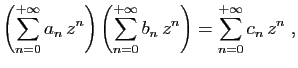
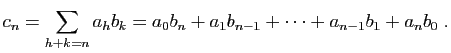
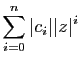
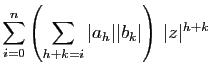
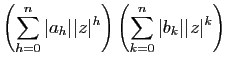
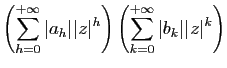
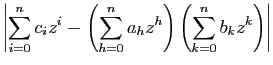
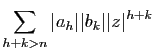
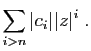
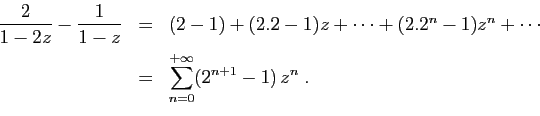
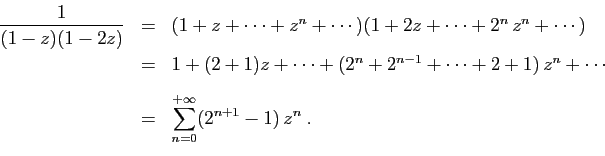
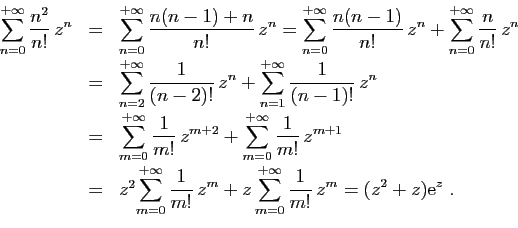
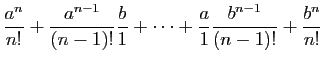
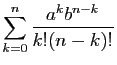
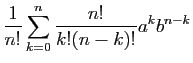
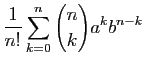
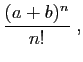
![]() a donc pour somme
a donc pour somme
![]() , et sa
valeur en
, et sa
valeur en ![]() est
est ![]() .
.![]() Dans la proposition précédente, nous avons remplacé
Dans la proposition précédente, nous avons remplacé ![]() par
par ![]() et
et ![]() dans la série exponentielle. Remplacer la variable
dans la série exponentielle. Remplacer la variable ![]() par
une fonction de celle-ci est une opération que l'on utilise
fréquemment. En voici deux exemples. Pour tout
par
une fonction de celle-ci est une opération que l'on utilise
fréquemment. En voici deux exemples. Pour tout ![]() tel que
tel que ![]() ,
on a :
,
on a :
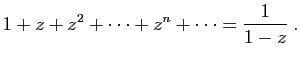
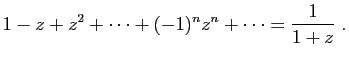
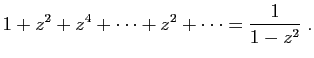
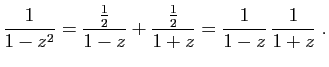
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales