Pour terminer, nous allons donner un petit aperçu de l'intérêt
des séries entières comme technique de résolution d'équations
récurrentes ou différentielles.
L'équation suivante se
rencontre dans l'analyse de certains algorithmes de tri.
avec 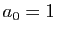 . Comment obtenir une expression explicite de
. Comment obtenir une expression explicite de
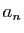 ? Introduisons la série entière
? Introduisons la série entière
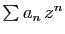 et notons
et notons 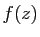 sa somme.
sa somme.
Pour obtenir une équation en  , on multiplie l'équation de
récurrence par
, on multiplie l'équation de
récurrence par 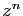 et on somme sur
et on somme sur 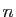 .
.
Il s'agit maintenant d'en déduire une équation en  . Pour cela
observons que le premier terme de la série est
. Pour cela
observons que le premier terme de la série est
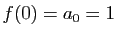 . On a
donc :
. On a
donc :
On en déduit l'équation suivante.
dont la solution est :
Il suffit alors de développer  en série entière pour
retrouver les
en série entière pour
retrouver les 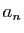 .
.
On obtient donc
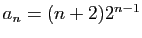 .
.
Voici un exemple plus compliqué. Le nombre 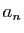 d'arbres binaires enracinés à
d'arbres binaires enracinés à 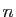 sommets vérifie :
sommets vérifie :
avec 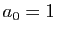 .
Notons
.
Notons 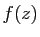 la somme de la série
la somme de la série
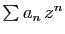 . On multiplie
l'équation de récurrence par
. On multiplie
l'équation de récurrence par 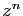 et on somme pour obtenir :
et on somme pour obtenir :
soit :
Des deux solutions de cette équation, seule celle qui vaut 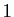 en 0 nous
intéresse :
en 0 nous
intéresse :
Il reste à développer 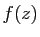 en série entière, en utilisant
le développement de
en série entière, en utilisant
le développement de
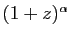 . On obtient :
. On obtient :
Considérons maintenant l'équation
différentielle suivante.
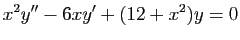 |
(E) |
Cherchons des solutions de (E) développables en série
entière :
En reportant ces séries dans l'équation (E), on obtient :
On commence par effectuer les changements d'indices nécessaires
pour ramener tous les termes à 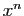 .
.
Si une fonction développable en série entière est nulle, ses
coefficients doivent être nuls : on en déduit des équations
particulières pour les premiers termes, et une équation de
récurrence générale pour les termes suivants.
Les trois premières équations donnent
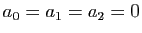 . La
quatrième s'écrit :
. La
quatrième s'écrit :
Pour 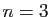 et
et 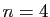 , elle n'apporte aucune information. Mais pour
, elle n'apporte aucune information. Mais pour
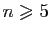 , elle permet d'exprimer tous les coefficients de la série
en fonction de
, elle permet d'exprimer tous les coefficients de la série
en fonction de 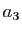 et
et 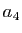 . Calculons d'abord les termes impairs :
. Calculons d'abord les termes impairs :
Par récurrence, on en déduit :
On calcule de la même façon les termes pairs :
Soit par récurrence :
La série
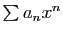 a un rayon de convergence
infini (application du corollaire 1).
En sommant, on obtient :
a un rayon de convergence
infini (application du corollaire 1).
En sommant, on obtient :
Les deux fonctions
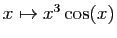 et
et
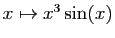 constituent une famille libre daans l'espace vectoriel des fonctions,
donc leurs combinaisons linéaires constituent
un espace vectoriel de dimension 2.
Comme l'équation (E) est linéaire et du second ordre, nous avons
trouvé toutes ses solutions sous forme de séries entières (ce
n'est pas toujours le cas).
constituent une famille libre daans l'espace vectoriel des fonctions,
donc leurs combinaisons linéaires constituent
un espace vectoriel de dimension 2.
Comme l'équation (E) est linéaire et du second ordre, nous avons
trouvé toutes ses solutions sous forme de séries entières (ce
n'est pas toujours le cas).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
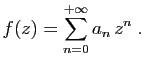
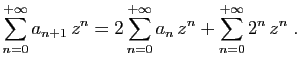
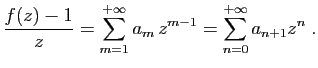
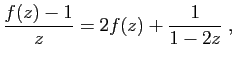
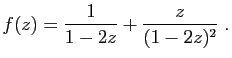
![]() d'arbres binaires enracinés à
d'arbres binaires enracinés à ![]() sommets vérifie :
sommets vérifie :
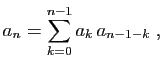
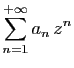
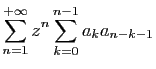
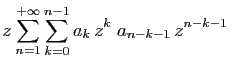
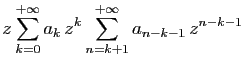
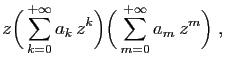
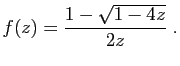
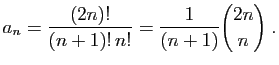
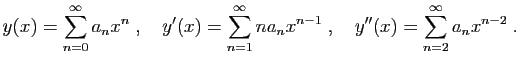
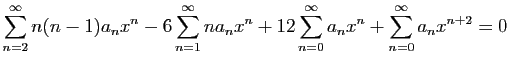
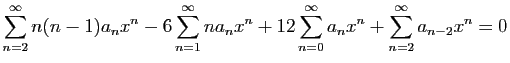
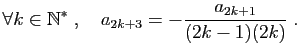
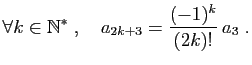
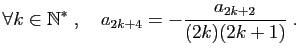
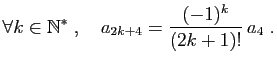
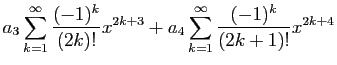
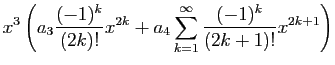
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales