Nous allons maintenant étudier les propriétés de la somme d'une
série entière, vue comme une fonction de la variable 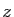 . Afin de
ne pas compliquer les définitions, nous supposons dans toute cette
section que
. Afin de
ne pas compliquer les définitions, nous supposons dans toute cette
section que 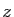 est réel. Les identités
obtenues restent vraies pour
est réel. Les identités
obtenues restent vraies pour 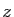 complexe, mais ce serait anticiper
inutilement sur des chapitres ultérieurs que de sortir du domaine réel.
complexe, mais ce serait anticiper
inutilement sur des chapitres ultérieurs que de sortir du domaine réel.
Un simple changement de variable permet de se ramener à des
développements en série entière en 0.
Proposition 3
La fonction 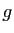 est développable en série entière en
est développable en série entière en 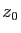 sur
sur
![$ ]z_0-R,z_0+R [$](img168.gif) , si et seulement si la fonction
, si et seulement si la fonction
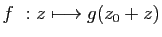 est développable
en série entière en 0 sur
est développable
en série entière en 0 sur
![$ ]\!-\!R,R [$](img172.gif) .
.
La vérification est immédiate, et ce résultat nous autorise
à ne plus considérer désormais que des développements en
série entière en 0.
Soit
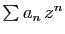 une série entière, et
une série entière, et 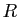 son rayon de
convergence. D'après le théorème 2,
la série converge pour tout réel
son rayon de
convergence. D'après le théorème 2,
la série converge pour tout réel 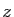 de valeur absolue
strictement inférieure à
de valeur absolue
strictement inférieure à 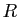 , soit sur l'intervalle
, soit sur l'intervalle
![$ ]\!-\!R,R [$](img172.gif) . Sa
somme est donc développable en série entière sur
. Sa
somme est donc développable en série entière sur
![$ ]\!-\!R,R [$](img172.gif) , par
définition.
, par
définition.
Le théorème suivant montre
qu'une fonction développable
en série entière, est indéfiniment dérivable. Ses
dérivées successives ainsi que ses primitives sont également
développables en série entière.
Théorème 4
Soit  une fonction développable en série entière, telle que
pour tout
une fonction développable en série entière, telle que
pour tout
![$ z\in]\!-\!R,R [$](img174.gif) ,
,
La fonction  est indéfiniment dérivable sur
est indéfiniment dérivable sur
![$ ]\!-\!R,R [$](img172.gif) .
Sa dérivée est la somme de la série dérivée terme
à terme, qui converge sur
.
Sa dérivée est la somme de la série dérivée terme
à terme, qui converge sur
![$ ]\!-\!R,R [$](img172.gif) .
.
La primitive de  qui s'annule en 0 est la somme de la série
intégrée terme à terme, qui converge sur
qui s'annule en 0 est la somme de la série
intégrée terme à terme, qui converge sur
![$ ]\!-\!R,R [$](img172.gif) .
.
Démonstration : Nous commençons par démontrer que la série
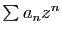 et la
série dérivée
et la
série dérivée
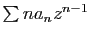 ont même rayon de
convergence. En effet :
ont même rayon de
convergence. En effet :
Donc :
d'où le résultat par le théorème 2.
La proposition 1 entraîne que la convergence est
uniforme sur tout intervalle ![$ [-\!r,r]$](img181.gif) inclus dans
inclus dans
![$ ]\!-\!R,R [$](img172.gif) . Si
une suite de fonctions dérivables converge uniformément sur un intervalle,
ainsi que la suite des dérivées, alors la limite de la suite est
dérivable à l'intérieur de l'intervalle, et sa dérivée est
la limite des dérivées. Ceci
entraîne que la fonction
. Si
une suite de fonctions dérivables converge uniformément sur un intervalle,
ainsi que la suite des dérivées, alors la limite de la suite est
dérivable à l'intérieur de l'intervalle, et sa dérivée est
la limite des dérivées. Ceci
entraîne que la fonction  est dérivable sur
tout intervalle
est dérivable sur
tout intervalle
![$ ]\!-\!r,r [$](img182.gif) inclus dans
inclus dans
![$ ]\!-\!R,R [$](img172.gif) , donc sur
, donc sur
![$ ]\!-\!R,R [$](img172.gif) . Par récurrence,
. Par récurrence,  est donc indéfiniment
dérivable sur
est donc indéfiniment
dérivable sur
![$ ]\!-\!R,R [$](img172.gif) .
En appliquant le résultat de dérivabilité à la série
primitive, on obtient la seconde partie du théorème.
.
En appliquant le résultat de dérivabilité à la série
primitive, on obtient la seconde partie du théorème.  Par exemple la fonction
Par exemple la fonction
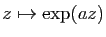 ,
est développable en série entière sur
,
est développable en série entière sur
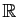 .
.
Sa dérivée est :
Le développement en série entière sur
![$ ]\!-\!1,1 [$](img190.gif) de
la fonction
de
la fonction
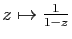 est
est 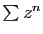 . Sa dérivée est :
. Sa dérivée est :
On pourrait aussi obtenir ce résultat en effectuant le produit de
la série 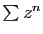 par elle-même.
On peut aussi calculer la primitive :
par elle-même.
On peut aussi calculer la primitive :
En remplaçant 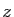 par
par 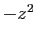 dans la série géométrique, puis
en prenant la primitive, on obtient les développements en série
entière de
dans la série géométrique, puis
en prenant la primitive, on obtient les développements en série
entière de
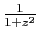 et
et
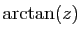 .
.
En appliquant de manière itérée le théorème 4 aux
dérivées successives de  , on peut donc calculer leurs
développements en série entière. On en déduit en particulier
l'expression du développement de
, on peut donc calculer leurs
développements en série entière. On en déduit en particulier
l'expression du développement de  en fonction des dérivées
successives, évaluées en
en fonction des dérivées
successives, évaluées en 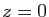 : vous connaissez déjà le
polynôme de Taylor.
: vous connaissez déjà le
polynôme de Taylor.
Corollaire 2
Si  est développable en série entière sur
est développable en série entière sur
![$ ]\!-\!R,R [$](img172.gif) , alors son
développement est :
, alors son
développement est :
Démonstration : Si
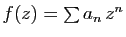 , alors f(0) est le premier terme de la
série :
, alors f(0) est le premier terme de la
série : 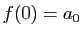 . Mais le
théorème 4 donne aussi :
. Mais le
théorème 4 donne aussi :
dont le premier terme est 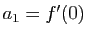 . La dérivée seconde est :
. La dérivée seconde est :
dont le premier terme est
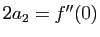 . Par récurrence, la
dérivée
. Par récurrence, la
dérivée 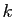 -ième est :
-ième est :
dont le premier terme est
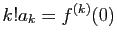 . D'où le résultat.
. D'où le résultat.
Définition 4
Si  est indéfiniment dérivable sur
est indéfiniment dérivable sur
![$ ]\!-\!R,R [$](img172.gif) , on appelle
, on appelle série de Taylor
de  en 0 la série
en 0 la série
Si  est développable en série entière sur
est développable en série entière sur
![$ ]\!-\!R,R [$](img172.gif) , alors
, alors  est indéfiniment dérivable à tout ordre au voisinage de 0, et
donc admet un développement limité en 0 à tout ordre. Le
développement limité à l'ordre
est indéfiniment dérivable à tout ordre au voisinage de 0, et
donc admet un développement limité en 0 à tout ordre. Le
développement limité à l'ordre 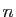 de
de  est la somme partielle
d'ordre
est la somme partielle
d'ordre 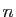 de sa série de Taylor.
de sa série de Taylor.
Malheureusement, la réciproque est fausse : il peut se faire que  admette un développement limité à tous ordres au voisinage de
0, sans que
admette un développement limité à tous ordres au voisinage de
0, sans que  soit somme de sa série de Taylor. L'exemple
classique est :
soit somme de sa série de Taylor. L'exemple
classique est :
Pour tout
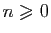 , on a :
, on a :
Donc
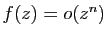 , pour tout
, pour tout 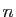 . On en déduit que
. On en déduit que  ainsi que
toutes ses dérivées sont prolongeables par continuité par 0 en
0, et que le développement limité de
ainsi que
toutes ses dérivées sont prolongeables par continuité par 0 en
0, et que le développement limité de  à tout ordre est
nul. Pourtant, bien que la série de Taylor de
à tout ordre est
nul. Pourtant, bien que la série de Taylor de  soit nulle,
soit nulle,  n'est pas identiquement nulle.
n'est pas identiquement nulle.
Nous allons donner une condition suffisante pour qu'une fonction
indéfiniment dérivable soit développable en série entière.
Pour cela nous utilisons une formule de Taylor qui donne une
expression explicite du reste, la formule de Taylor avec reste
intégral.
Théorème 5
Soit  une fonction de classe
une fonction de classe
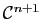 sur
sur
![$ ]\!-\!R,R [$](img172.gif) (c'est-à-dire
(c'est-à-dire 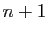 fois dérivable, de dérivée
fois dérivable, de dérivée 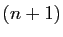 -ième
continue). Pour tout
-ième
continue). Pour tout
![$ z\in]\!-\!R,R [$](img174.gif) on a :
on a :
avec
Démonstration : Pour 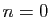 , la formule est vraie :
, la formule est vraie :
Intégrons 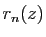 par parties.
par parties.
Si on suppose la formule vraie à l'ordre 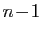 , alors :
, alors :
Le résultat est donc vrai à l'ordre 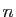 .
. Pour qu'une fonction indéfiniment dérivable soit développable en série
entière, il est nécessaire et suffisant que le reste
Pour qu'une fonction indéfiniment dérivable soit développable en série
entière, il est nécessaire et suffisant que le reste 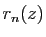 de la
formule de Taylor tende vers 0. C'est vrai en particulier si les
dérivées successives sont uniformément bornées, avec des
bornes croissant au plus géométriquement.
de la
formule de Taylor tende vers 0. C'est vrai en particulier si les
dérivées successives sont uniformément bornées, avec des
bornes croissant au plus géométriquement.
Démonstration : Sous cette hypothèse, on peut borner le reste 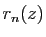 de la
façon suivante.
de la
façon suivante.
Le reste 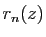 tend donc vers 0 quand
tend donc vers 0 quand 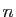 tend vers l'infini.
tend vers l'infini. Cette proposition s'applique par exemple aux fonctions
Cette proposition s'applique par exemple aux fonctions 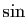 et
et
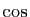 (dont toutes les dérivées sont bornées),
mais aussi à la plupart des fonctions usuelles.
(dont toutes les dérivées sont bornées),
mais aussi à la plupart des fonctions usuelles.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
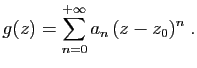
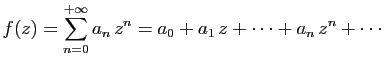
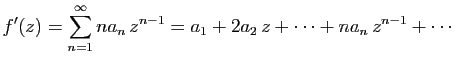
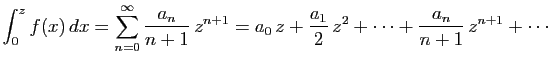
![$\displaystyle \mathop{\lim\sup}_{n\rightarrow\infty}\sqrt[n]{\vert na_n\vert}
=
\mathop{\lim\sup}_{n\rightarrow\infty}\sqrt[n]{\vert a_n\vert}\;,
$](img180.gif)
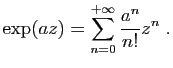
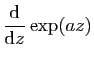
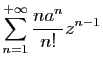
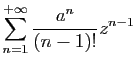
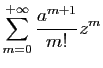
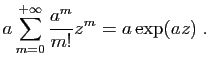
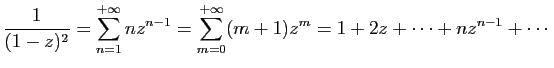
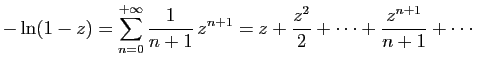
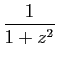
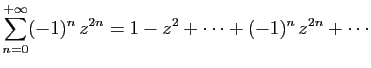
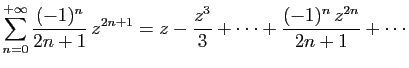
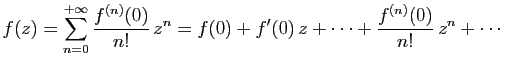
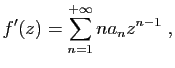
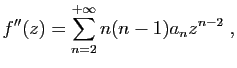
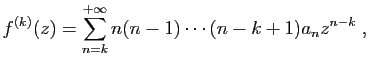
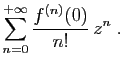
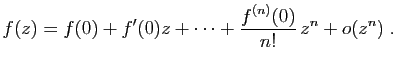
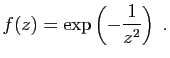
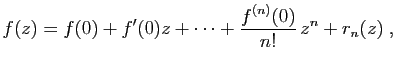
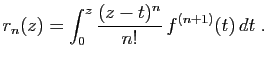
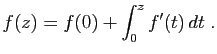
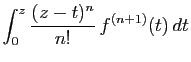
![$\displaystyle \displaystyle{\left[\frac{(z-t)^n}{n!} f^{(n)}(t)\right]_0^z
+\int_0^z \frac{(z-t)^{n-1}}{(n-1)!} f^{(n)}(t) dt}$](img227.gif)
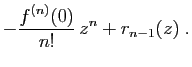
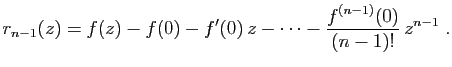
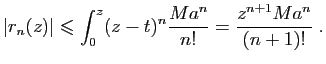
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales