Dans cette section,  est un réel quelconque, et nous considérons la
limite (bilatérale) d'une fonction
est un réel quelconque, et nous considérons la
limite (bilatérale) d'une fonction  en
en  , au sens de la définition
3. Toutes les fonctions sont supposées
être définies au voisinage de
, au sens de la définition
3. Toutes les fonctions sont supposées
être définies au voisinage de  , sauf
peut-être en
, sauf
peut-être en  .
.
Tous les résultats de la section valent aussi
pour des limites à gauche, à droite, en 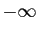 et en
et en
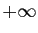 . L'adaptation des démonstrations aux autres types de
limite est un exercice conseillé.
. L'adaptation des démonstrations aux autres types de
limite est un exercice conseillé.
Le résultat de base pour comparer deux limites est le suivant.
Démonstration : Supposons
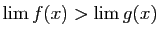 . Alors la limite en
. Alors la limite en
 de la fonction
de la fonction 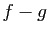 est strictement positive.
Notons
est strictement positive.
Notons 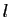 cette limite. Il existe
cette limite. Il existe 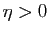 tel
que
tel
que
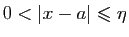 entraîne
entraîne
![$ f(x)-g(x)\in
[\frac{l}{2},\frac{3l}{2}]$](img179.gif) ,
donc
,
donc
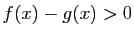 , ce qui contredit l'hypothèse.
, ce qui contredit l'hypothèse. Le fait de supposer
Le fait de supposer 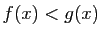 ne renforce pas la conclusion :
bien que
ne renforce pas la conclusion :
bien que  pour tout
pour tout
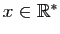 ,
,
Le théorème 5 ne permet pas de démontrer
que l'une des deux fonctions  ou
ou 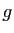 converge en
converge en  .
Pour cela, on utilise souvent le résultat suivant.
.
Pour cela, on utilise souvent le résultat suivant.
Théorème 6
Soient  et
et 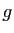 deux fonctions telles que
deux fonctions telles que 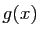 tend vers 0 quand
tend vers 0 quand
 tend vers
tend vers  . S'il existe un intervalle ouvert
. S'il existe un intervalle ouvert 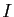 contenant
contenant  tel que pour tout
tel que pour tout  ,
,
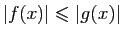 ,
alors
,
alors 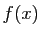 tend vers 0 en
tend vers 0 en  .
.
Démonstration : Pour tout
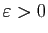 , il existe
, il existe 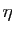 tel que pour
tel que pour
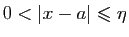 :
:
d'où le résultat. On en déduit le corollaire suivant.
On en déduit le corollaire suivant.
Démonstration : Il suffit d'appliquer le théorème 6
aux deux fonctions 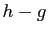 et
et 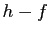 .
.  Soit par exemple
Soit par exemple
Posons 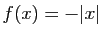 ,
, 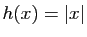 . Les deux fonctions
. Les deux fonctions  et
et 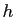 tendent vers
0 en 0, et pour tout
tendent vers
0 en 0, et pour tout
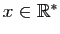 ,
,
Donc 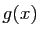 tend vers 0 quand
tend vers 0 quand  tend vers 0, comme
tend vers 0, comme  et
et 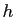 (cf. figure 1).
(cf. figure 1).
La comparaison vaut aussi pour les limites infinies.
Théorème 7
Soient  un réel,
un réel,  et
et 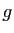 deux fonctions définies sur un
intervalle ouvert
deux fonctions définies sur un
intervalle ouvert 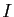 contenant
contenant  . Supposons que,
pour tout
. Supposons que,
pour tout  ,
,
 .
.
Si
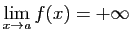
alors
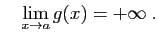
Si
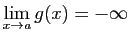
alors
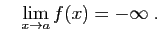
Démonstration : Pour tout 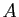 , il existe
, il existe 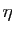 tel que pour
tel que pour
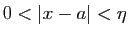 :
:
donc 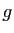 tend vers
tend vers 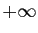 si
si  tend vers
tend vers 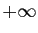 . La
démonstration de l'autre
affirmation est analogue.
. La
démonstration de l'autre
affirmation est analogue. Le vocabulaire de la comparaison des fonctions est analogue à celui
des suites, avec la difficulté supplémentaire qu'il faut toujours
savoir de quelle limite il s'agit (bilatérale, à gauche, à
droite, en
Le vocabulaire de la comparaison des fonctions est analogue à celui
des suites, avec la difficulté supplémentaire qu'il faut toujours
savoir de quelle limite il s'agit (bilatérale, à gauche, à
droite, en 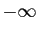 ou en
ou en 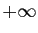 ). Nous écrivons la définition
ci-dessous pour des limites bilatérales en
). Nous écrivons la définition
ci-dessous pour des limites bilatérales en  , elle s'adapte sans
problème aux 4 autres types de limites.
, elle s'adapte sans
problème aux 4 autres types de limites.
Très souvent, on appliquera ces définitions pour une fonction 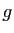 non nulle au voisinage de
non nulle au voisinage de  , sauf peut-être en
, sauf peut-être en  ;
dans ce cas, la comparaison se lit sur le rapport
;
dans ce cas, la comparaison se lit sur le rapport
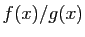 .
.
Par exemple, au voisinage de 0 :
Au voisinage de 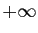 :
:
Insistons sur la nécessité de bien préciser le type de limite
que l'on considère. Le plus souvent, il s'agira de limites en
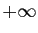 ou de limites à droite en 0. On passe des unes aux
autres en remplaçant la variable
ou de limites à droite en 0. On passe des unes aux
autres en remplaçant la variable  par
par 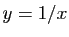 . Pour étudier
une limite en
. Pour étudier
une limite en  , on se ramène à une limite en 0 en posant
, on se ramène à une limite en 0 en posant
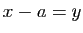 . Le changement de variable
. Le changement de variable 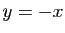 permet de passer des limites
à gauche aux limites à droite, des limites en
permet de passer des limites
à gauche aux limites à droite, des limites en 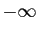 aux
limites en
aux
limites en 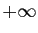 .
.
Observons que
 entraîne
entraîne
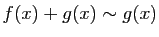 , ce qui
est particulièrement utile pour les polynômes.
Les équivalents sont souvent utilisés pour le calcul de limites de
produits ou de quotients, car si
, ce qui
est particulièrement utile pour les polynômes.
Les équivalents sont souvent utilisés pour le calcul de limites de
produits ou de quotients, car si
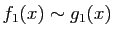 , et
, et
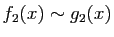 alors
alors
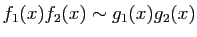 . Par contre il ne faut pas les
utiliser pour des sommes. Par exemple, au voisinage de
. Par contre il ne faut pas les
utiliser pour des sommes. Par exemple, au voisinage de 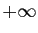 :
:
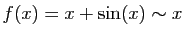
et
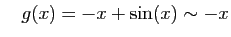
Pourtant,  n'est pas équivalent à 0.
n'est pas équivalent à 0.
Soit  la fonction définie sur
la fonction définie sur
![$ ]0,+\infty[$](img225.gif) par :
par :
Commençons par les limites à droite en 0. Le
numérateur tend vers 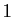 en 0. Pour le dénominateur
en 0. Pour le dénominateur
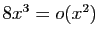 , donc
, donc
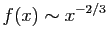 :
:
Considérons maintenant les limites en 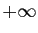 .
Puisque
.
Puisque
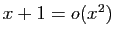 ,
,
 et
et
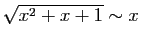 .
Pour le dénominateur,
.
Pour le dénominateur,
![$ \sqrt[3]{8x^3+x^2}\sim 2x$](img233.gif) , donc
, donc
 tend vers
tend vers 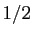 .
.
Nous admettrons pour l'instant les équivalents suivants au voisinage
de 0, qui seront justifiés plus loin. Vous devez les connaître
par c ur.
ur.
Nous rassemblons dans la section suivante d'autres limites classiques
concernant l'exponentielle et le logarithme, qu'il est également bon
de connaître.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et en
et en
![]() . L'adaptation des démonstrations aux autres types de
limite est un exercice conseillé.
. L'adaptation des démonstrations aux autres types de
limite est un exercice conseillé.
![]() ou
ou ![]() converge en
converge en ![]() .
Pour cela, on utilise souvent le résultat suivant.
.
Pour cela, on utilise souvent le résultat suivant.
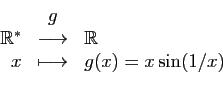
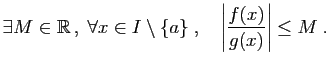
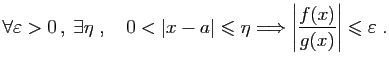
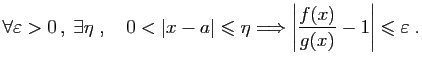
![]() entraîne
entraîne
![]() , ce qui
est particulièrement utile pour les polynômes.
Les équivalents sont souvent utilisés pour le calcul de limites de
produits ou de quotients, car si
, ce qui
est particulièrement utile pour les polynômes.
Les équivalents sont souvent utilisés pour le calcul de limites de
produits ou de quotients, car si
![]() , et
, et
![]() alors
alors
![]() . Par contre il ne faut pas les
utiliser pour des sommes. Par exemple, au voisinage de
. Par contre il ne faut pas les
utiliser pour des sommes. Par exemple, au voisinage de ![]() :
:
![]() la fonction définie sur
la fonction définie sur
![]() par :
par :
![$\displaystyle f(x) = \frac{\sqrt{x^2+x+1}}{\sqrt[3]{8x^3+x^2}}\;.
$](img226.gif)
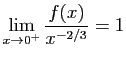
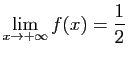
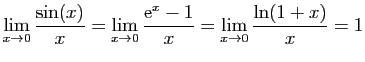
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales