Une fonction  peut converger vers une limite finie, comme nous
l'avons vu précédemment, ou bien
peut converger vers une limite finie, comme nous
l'avons vu précédemment, ou bien 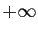 ou
ou 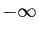 . De plus
les valeurs de la variable, qui approchaient
. De plus
les valeurs de la variable, qui approchaient  des deux côtés
dans les définitions précédentes, peuvent ne l'approcher que
d'un seul côté : ce sont les notions de
limite à gauche, et de limite
à droite. On peut aussi chercher une limite quand
des deux côtés
dans les définitions précédentes, peuvent ne l'approcher que
d'un seul côté : ce sont les notions de
limite à gauche, et de limite
à droite. On peut aussi chercher une limite quand 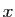 tend vers
tend vers
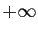 et
et 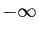 . Au total, ce ne sont pas moins de
. Au total, ce ne sont pas moins de 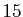 définitions différentes que nous devons donner. Vous
reconnaîtrez dans ces définitions un principe général :
définitions différentes que nous devons donner. Vous
reconnaîtrez dans ces définitions un principe général :
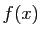 tend vers
tend vers 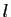 (fini ou infini) quand
(fini ou infini) quand 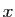 tend vers
tend vers  (fini ou infini), si pour tout voisinage
(fini ou infini), si pour tout voisinage 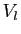 de
de 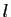 , il existe un voisinage
, il existe un voisinage
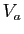 de
de  tel que
tel que
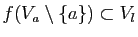 . La
définition précise de la notion de voisinage relève de la
topologie, et dépasse le cadre de ce cours. Un voisinage
de
. La
définition précise de la notion de voisinage relève de la
topologie, et dépasse le cadre de ce cours. Un voisinage
de 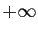 sera compris comme un intervalle de la forme
sera compris comme un intervalle de la forme
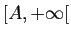 . De même, un voisinage de
. De même, un voisinage de 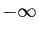 sera un
intervalle de la forme
sera un
intervalle de la forme
![$ ]-\infty,A]$](img133.gif) . Un «voisinage à gauche» d'un
réel
. Un «voisinage à gauche» d'un
réel  sera un intervalle du type
sera un intervalle du type
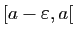 , tandis qu'un
«voisinage à droite» sera de la forme
, tandis qu'un
«voisinage à droite» sera de la forme
![$ ]a,a+\varepsilon ]$](img135.gif) . Nous donnons les
différentes définitions sous forme de tableaux. Plutôt que
d'apprendre les 5 tableaux par c
. Nous donnons les
différentes définitions sous forme de tableaux. Plutôt que
d'apprendre les 5 tableaux par c ur, il est conseillé d'en
comprendre le principe pour être capable de retrouver ces
définitions en cas de besoin.
ur, il est conseillé d'en
comprendre le principe pour être capable de retrouver ces
définitions en cas de besoin.
La limite bilatérale des sections précédentes peut se
caractériser en termes de limites à gauche et à droite.
Proposition 2
Soit  une fonction de
une fonction de
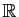 dans
dans
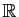 et
et  un réel. La
fonction
un réel. La
fonction  admet
admet 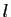 pour limite en
pour limite en  , si et
seulement si elle admet
, si et
seulement si elle admet 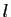 pour limite à gauche et à droite en
pour limite à gauche et à droite en
 .
.
Démonstration : Nous le démontrons pour une limite finie. Ce qui suit est facile à
adapter à une limite infinie.
La condition nécessaire est évidente au vu des
définitions. Pour la condition suffisante, supposons
Fixons
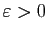 .
Il existe
.
Il existe 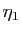 et
et 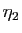 tels que
tels que
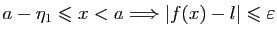
et
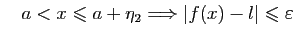
Prenons
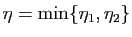 , alors
, alors

Voici maintenant les définitions des limites en 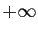 et
et 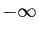 .
.
Pour chacune de ces définitions, il existe une caractérisation en
termes de suites, analogue au théorème 1. Par
exemple, la limite à gauche de  en
en  vaut
vaut 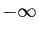 si et
seulement si pour toute suite
si et
seulement si pour toute suite 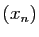 convergeant vers
convergeant vers  et telle
que pour tout
et telle
que pour tout 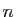 ,
, 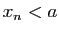 , la suite
, la suite 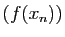 tend vers
tend vers
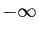 . Nous laissons au lecteur le soin de démontrer, à titre
d'exercice, chacune de ces caractérisations,
sur le modèle du théorème 1.
. Nous laissons au lecteur le soin de démontrer, à titre
d'exercice, chacune de ces caractérisations,
sur le modèle du théorème 1.
En ce qui concerne les opérations, le théorème
2 s'étend aux limites à gauche,
à droite, en 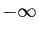 et en
et en 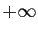 , sans aucune difficulté. Les
seuls problèmes viennent des limites éventuellement infinies.
Dans le cas où les limites de
, sans aucune difficulté. Les
seuls problèmes viennent des limites éventuellement infinies.
Dans le cas où les limites de  et
et 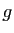 peuvent être
infinies, différentes situations peuvent se produire pour la somme
et le produit. Nous les résumons dans les tableaux
1 et 2.
Dans ces deux tableaux,
peuvent être
infinies, différentes situations peuvent se produire pour la somme
et le produit. Nous les résumons dans les tableaux
1 et 2.
Dans ces deux tableaux, 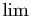 désigne indifféremment une limite
bilatérale, à gauche, à droite, en
désigne indifféremment une limite
bilatérale, à gauche, à droite, en 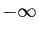 ou en
ou en 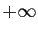 (du
même type pour
(du
même type pour  et
et 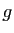 ).
Les points d'interrogations sont des formes indéterminées : tous les cas
sont possibles. Par exemple :
).
Les points d'interrogations sont des formes indéterminées : tous les cas
sont possibles. Par exemple :
-
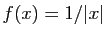 ,
,
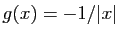 :
: 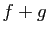 tend vers 0 quand
tend vers 0 quand 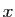 tend vers 0.
tend vers 0.
-
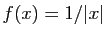 ,
,
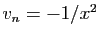 :
: 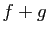 tend vers
tend vers 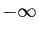 quand
quand 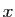 tend
vers 0.
tend
vers 0.
-
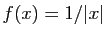 ,
,
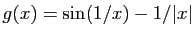 :
: 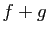 n'a pas de limite en 0.
n'a pas de limite en 0.
Tableau 1:
Limites possibles de 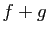 en fonction des limites de
en fonction des limites de
 et
et 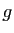 .
.
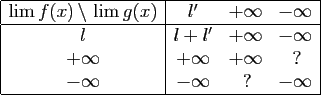 |
Tableau 2:
Limites possibles de 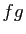 en fonction des limites de
en fonction des limites de
 et
et 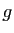 .
.
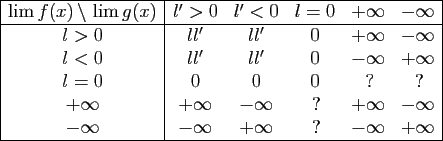 |
Mises à part les formes indéterminées,
chacune des cases des tableaux 1 et
2 résume 5 théorèmes : un pour
chacun des différents types de limites. Il est
conseillé au lecteur de les
démontrer, soit directement sur le modèle
du théorème 2, soit en utilisant la
caractérisation par les suites évoquée plus haut.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![\begin{displaymath}
\begin{array}{\vert l\vert l\vert l\vert}
\hline
\multicolum...
...tarrow 0} -1/\vert x\vert=-\infty}\ [1.5ex]
\hline
\end{array}\end{displaymath}](img137.gif)
![\begin{displaymath}
\begin{array}{\vert l\vert l\vert l\vert}
\hline
\multicolum...
..._{x\rightarrow 0^{-}} 1/x=-\infty}\ [1.5ex]
\hline
\end{array}\end{displaymath}](img138.gif)
![\begin{displaymath}
\begin{array}{\vert l\vert l\vert l\vert}
\hline
\multicolum...
...{x\rightarrow 0^{+}} -1/x=-\infty}\ [1.5ex]
\hline
\end{array}\end{displaymath}](img139.gif)
![]() et
et ![]() .
.
![\begin{displaymath}
\begin{array}{\vert l\vert l\vert l\vert}
\hline
\multicolum...
..._{x\rightarrow -\infty} x=-\infty}\ [1.5ex]
\hline
\end{array}\end{displaymath}](img145.gif)
![\begin{displaymath}
\begin{array}{\vert l\vert l\vert l\vert}
\hline
\multicolum...
...{x\rightarrow +\infty} -x=-\infty}\ [1.5ex]
\hline
\end{array}\end{displaymath}](img146.gif)
![]() et en
et en ![]() , sans aucune difficulté. Les
seuls problèmes viennent des limites éventuellement infinies.
Dans le cas où les limites de
, sans aucune difficulté. Les
seuls problèmes viennent des limites éventuellement infinies.
Dans le cas où les limites de ![]() et
et ![]() peuvent être
infinies, différentes situations peuvent se produire pour la somme
et le produit. Nous les résumons dans les tableaux
1 et 2.
Dans ces deux tableaux,
peuvent être
infinies, différentes situations peuvent se produire pour la somme
et le produit. Nous les résumons dans les tableaux
1 et 2.
Dans ces deux tableaux, ![]() désigne indifféremment une limite
bilatérale, à gauche, à droite, en
désigne indifféremment une limite
bilatérale, à gauche, à droite, en ![]() ou en
ou en ![]() (du
même type pour
(du
même type pour ![]() et
et ![]() ).
Les points d'interrogations sont des formes indéterminées : tous les cas
sont possibles. Par exemple :
).
Les points d'interrogations sont des formes indéterminées : tous les cas
sont possibles. Par exemple :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales