Le texte de Cauchy définit la continuité d'une fonction sur un
intervalle («entre deux limites»). Il confond en fait deux notions,
qui ne seront distinguées que beaucoup plus tard, en particulier
par Eduard Heine (1821-1881) en 1872.
Soit  une fonction, définie sur un intervalle
une fonction, définie sur un intervalle
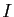 . Ecrivons d'abord que
. Ecrivons d'abord que  est continue sur
est continue sur 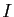 , au sens de la
définition 6.
, au sens de la
définition 6.
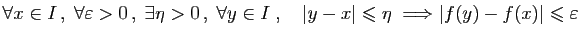 |
(2) |
Définition 7
On dit que  est uniformément continue sur
est uniformément continue sur 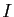 si
si
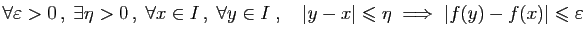 |
(3) |
Evidemment, (3) implique (2), mais la
réciproque est fausse en général.
La différence entre (2) et (3) est subtile. Dans
(2) la valeur de 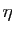 peut dépendre non seulement de
peut dépendre non seulement de
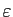 mais aussi de
mais aussi de  . Dans (3), elle ne peut dépendre
que de
. Dans (3), elle ne peut dépendre
que de
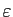 : pour un
: pour un
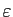 donné, on peut choisir le même
donné, on peut choisir le même
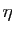 pour tous les points de l'intervalle.
pour tous les points de l'intervalle.
Examinons la fonction inverse sur ![$ I=]0,1]$](img697.gif) (cf. proposition
7).
(cf. proposition
7).
Soit  un point de
un point de ![$ ]0,1]$](img417.gif) et
et
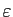 un réel strictement
compris entre 0 et
un réel strictement
compris entre 0 et 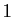 . L'image réciproque par
. L'image réciproque par  de
l'intervalle
de
l'intervalle
![$ [f(x)-\varepsilon ,f(x)+\varepsilon ]$](img699.gif) est l'intervalle :
est l'intervalle :
Cet intervalle contient  , et
, et
Posons
Alors, pour tout 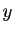 dans l'intervalle
dans l'intervalle
![$ [x-\eta_x,
x+\eta_x]$](img703.gif) ,
, 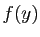 reste dans l'intervalle
reste dans l'intervalle
![$ [f(x)-\varepsilon ,f(x)+\varepsilon ]$](img699.gif) . De plus,
. De plus,
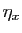 est le plus grand réel possédant cette
propriété. Observons que pour
est le plus grand réel possédant cette
propriété. Observons que pour
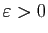 fixé,
fixé, 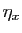 tend
vers 0 quand
tend
vers 0 quand  tend vers 0.
tend vers 0.
Bien sûr, pour n'importe quel
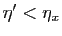 , l'implication
, l'implication
reste vraie. Mais il n'est pas possible de choisir un même 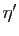 tel qu'elle reste vraie pour tous les
tel qu'elle reste vraie pour tous les  de
de ![$ ]0,1]$](img417.gif) : la
fonction
: la
fonction  n'est pas uniformément continue sur
n'est pas uniformément continue sur ![$ ]0,1]$](img417.gif) .
.
Examinons maintenant la fonction racine carrée sur le même
intervalle ![$ I=]0,1]$](img697.gif) .
.
Soit  un point de
un point de ![$ ]0,1]$](img417.gif) et
et
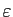 un réel strictement
compris entre 0 et
un réel strictement
compris entre 0 et 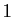 . Pour
. Pour
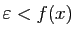 ,
l'image réciproque par
,
l'image réciproque par  de
l'intervalle
de
l'intervalle
![$ [f(x)-\varepsilon ,f(x)+\varepsilon ]$](img699.gif) est l'intervalle :
est l'intervalle :
Pour
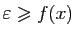 , c'est l'intervalle
, c'est l'intervalle
L'amplitude de ces intervalles dépend bien de  a priori.
Posons
a priori.
Posons
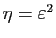 . Nous allons démontrer que pour tout
. Nous allons démontrer que pour tout
![$ x,y\in
]0,1]$](img715.gif) , si
, si
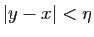 , alors
, alors
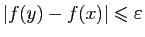 , ce qui entraîne que
, ce qui entraîne que  est uniformément continue sur
est uniformément continue sur  . Supposons
d'abord
. Supposons
d'abord
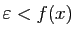 . Alors
. Alors
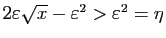 . Donc
l'intervalle
. Donc
l'intervalle
![$ f^{-1}([f(x)-\varepsilon ,f(x)+\varepsilon ])$](img719.gif) contient l'intervalle
contient l'intervalle
![$ [x-\eta,x+\eta]$](img720.gif) : si
: si 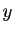 vérifie
vérifie
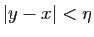 , alors
, alors
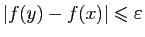 .
Supposons maintenant
.
Supposons maintenant
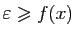 . Si
. Si 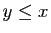 , alors
, alors
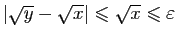 . Si
. Si
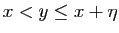 , alors
, alors
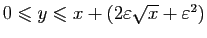 , donc
, donc
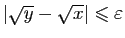 .
.
Le résultat suivant, que l'on appelle traditionnellement
théorème de Heine, a semble-t-il été démontré pour
la première fois par Dirichlet en 1862. Comme pour beaucoup de
théorèmes importants, son histoire est compliquée, au
point qu'il a été proposé de l'appeler «théorème de
Dirichlet-Heine-Weierstrass-Borel-Schoenflies-Lebesgue», par ordre
d'entrée en scène des mathématiciens qui l'ont raffiné ou
généralisé.
Théorème 14
Toute fonction continue sur un intervalle fermé borné est
uniformément continue.
Donc la fonction
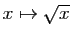 est uniformément continue sur
est uniformément continue sur
![$ [0,1]$](img405.gif) , tout comme la fonction
, tout comme la fonction
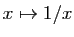 sur l'intervalle
sur l'intervalle
![$ [10^{-3},1]$](img727.gif) .
Démonstration : Soit
.
Démonstration : Soit ![$ [a,b]$](img295.gif) un intervalle fermé borné, et
un intervalle fermé borné, et  une fonction
continue sur
une fonction
continue sur ![$ [a,b]$](img295.gif) . Soit
. Soit
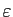 un réel strictement
positif. D'après (2), pour tout
un réel strictement
positif. D'après (2), pour tout ![$ x\in[a,b]$](img728.gif) , il existe un
réel strictement positif, que nous noterons
, il existe un
réel strictement positif, que nous noterons 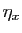 , tel que pour
tout
, tel que pour
tout
![$ y\in [a,b]$](img729.gif) ,
,
Pour tout  , considérons
l'intervalle ouvert
, considérons
l'intervalle ouvert
![$ ]x-\eta_x,x+\eta_x[$](img731.gif) , noté
, noté 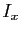 .
Le point crucial de la
démonstration est qu'il est possible d'extraire de cette famille
d'intervalles une famille finie, qui recouvre l'intervalle
.
Le point crucial de la
démonstration est qu'il est possible d'extraire de cette famille
d'intervalles une famille finie, qui recouvre l'intervalle ![$ [a,b]$](img295.gif) :
:
![$\displaystyle \exists m\in \mathbb{N} ,\;\exists x_1,\ldots,x_m\in[a,b]\;,\quad [a,b]\subset \bigcup_{i=1}^m I_{x_i}$](img733.gif) |
(4) |
Ceci est un cas particulier d'un résultat de topologie plus
général, le lemme de Borel-Lebesgue. Pour
le démontrer, la première étape consiste à montrer que pour un
certain entier 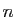 , tout intervalle de la forme
, tout intervalle de la forme
![$ ]y-1/n,y+1/n[$](img734.gif) est
inclus dans l'un des
est
inclus dans l'un des 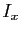 au moins.
au moins.
![$\displaystyle \exists n\in\mathbb{N} ,\;\forall y\in [a,b] ,\;\exists x\in[a,b]\;,\quad ]y-1/n,y+1/n[\subset I_x$](img735.gif) |
(5) |
Ecrivons la négation :
Pour tout 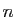 , soit
, soit 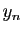 l'un des
l'un des 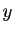 dont l'existence est affirmée
ci-dessus. Par le théorème de Bolzano-Weierstrass, on peut
extraire de la suite
dont l'existence est affirmée
ci-dessus. Par le théorème de Bolzano-Weierstrass, on peut
extraire de la suite 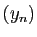 une sous-suite
une sous-suite
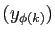 , qui
converge vers
, qui
converge vers ![$ c\in [a,b]$](img336.gif) . En particulier, aucun des intervalles
. En particulier, aucun des intervalles
![$ ]y_{\phi(k)}-1/\phi(k),y_{\phi(k)}+1/\phi(k)[$](img740.gif) n'est inclus dans
n'est inclus dans
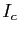 , ce qui est impossible si
, ce qui est impossible si 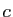 est la limite de
est la limite de
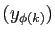 .
.
En utilisant (5), nous allons démontrer
(4) par l'absurde. Soit 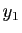 un point de
un point de ![$ [a,b]$](img295.gif) . Il
existe
. Il
existe 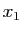 tel que
tel que
![$ ]y_1-1/n,y_1+1/n[\subset I_{x_1}$](img743.gif) . Comme
. Comme
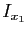 ne recouvre pas
ne recouvre pas ![$ [a,b]$](img295.gif) , il existe un point
, il existe un point 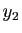 de
de ![$ [a,b]$](img295.gif) qui n'appartient pas à
qui n'appartient pas à 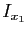 . Ce point est à distance au moins
. Ce point est à distance au moins
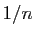 de
de 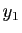 . Il existe un point
. Il existe un point 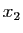 tel que
tel que
![$ ]y_2-1/n,y_2+1/n[\subset I_{x_2}$](img748.gif) . La réunion
. La réunion
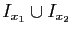 ne recouvre pas
ne recouvre pas ![$ [a,b]$](img295.gif) . Donc il existe
. Donc il existe 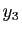 en dehors de
cette réunion :
en dehors de
cette réunion : 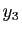 est à distance au moins
est à distance au moins 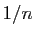 de
de 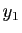 et
de
et
de 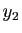 . Par récurrence, on construit ainsi une suite
. Par récurrence, on construit ainsi une suite 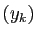 de points de
de points de ![$ [a,b]$](img295.gif) telle que deux quelconques de ses éléments sont
à distance au moins
telle que deux quelconques de ses éléments sont
à distance au moins 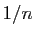 . En appliquant une fois de plus le
théorème de Bolzano-Weierstrass, une sous-suite de
. En appliquant une fois de plus le
théorème de Bolzano-Weierstrass, une sous-suite de 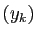 devrait
converger, d'où la contradiction.
devrait
converger, d'où la contradiction.
Puisque les intervalles ouverts
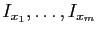 recouvrent
recouvrent
![$ [a,b]$](img295.gif) , il existe
, il existe 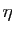 tel que si
tel que si
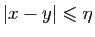 , alors
, alors  et
et 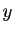 appartiennent à un même intervalle
appartiennent à un même intervalle 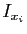 . Si c'est le cas,
. Si c'est le cas,
par définition de 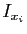 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() (cf. proposition
7).
(cf. proposition
7).
![\begin{displaymath}
\begin{array}{rcl}
&f&\\
]0,1]&\longrightarrow&\mathbb{R}\\
x&\longmapsto&f(x)=1/x
\end{array}\end{displaymath}](img698.gif)
![$\displaystyle f^{-1}([f(x)-\varepsilon ,f(x)+\varepsilon ])=
\left[\frac{1}{f(x)+\varepsilon },\frac{1}{f(x)-\varepsilon }\right]
$](img700.gif)
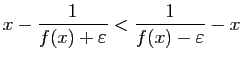
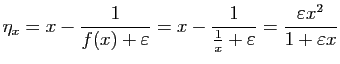
![]() , l'implication
, l'implication
![]() .
.
![\begin{displaymath}
\begin{array}{rcl}
&f&\\
]0,1]&\longrightarrow&\mathbb{R}\\
x&\longmapsto&f(x)=\sqrt{x}
\end{array}\end{displaymath}](img709.gif)
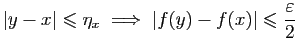
![]() un point de
un point de ![]() . Il
existe
. Il
existe ![]() tel que
tel que
![]() . Comme
. Comme
![]() ne recouvre pas
ne recouvre pas ![]() , il existe un point
, il existe un point ![]() de
de ![]() qui n'appartient pas à
qui n'appartient pas à ![]() . Ce point est à distance au moins
. Ce point est à distance au moins
![]() de
de ![]() . Il existe un point
. Il existe un point ![]() tel que
tel que
![]() . La réunion
. La réunion
![]() ne recouvre pas
ne recouvre pas ![]() . Donc il existe
. Donc il existe ![]() en dehors de
cette réunion :
en dehors de
cette réunion : ![]() est à distance au moins
est à distance au moins ![]() de
de ![]() et
de
et
de ![]() . Par récurrence, on construit ainsi une suite
. Par récurrence, on construit ainsi une suite ![]() de points de
de points de ![]() telle que deux quelconques de ses éléments sont
à distance au moins
telle que deux quelconques de ses éléments sont
à distance au moins ![]() . En appliquant une fois de plus le
théorème de Bolzano-Weierstrass, une sous-suite de
. En appliquant une fois de plus le
théorème de Bolzano-Weierstrass, une sous-suite de ![]() devrait
converger, d'où la contradiction.
devrait
converger, d'où la contradiction.
![]() recouvrent
recouvrent
![]() , il existe
, il existe ![]() tel que si
tel que si
![]() , alors
, alors ![]() et
et ![]() appartiennent à un même intervalle
appartiennent à un même intervalle ![]() . Si c'est le cas,
. Si c'est le cas,
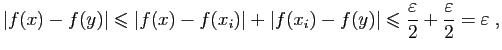
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales