Cauchy et les limites

Augustin-Louis Cauchy (1789-1857) est l'un des plus grands mathématiciens de tous les temps, ne serait-ce que par sa production impressionnante : pas moins de 789 articles, répartis en 27 volumes dans ses uvres complètes. Par contre, il n'a pas laissé un souvenir impérissable à ses étudiants. L'un d'eux écrit :

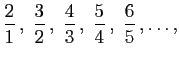
Ses cours étaient très confus, sautant brusquement d'une idée à une autre, d'une formule à la suivante, sans aucune tentative pour les connecter. Ses présentations étaient des nuages obscurs, illuminés de temps à autre par des éclairs de pur génie.

Royaliste convaincu, catholique dévot et militant, ses fortes opinions et son caractère difficile lui attirèrent de nombreuses inimitiés. Il dut même s'exiler pour un temps à Turin, puis à Prague, où l'ex-roi Charles X lui confia l'éducation scientifique de son petit fils. Mais là encore, «le prince montrant peu d'intérêt pour ses sujets. Cauchy s'énervait, et se mettrait à crier et à hurler».

Pourtant les cours polycopiés de Cauchy pour les élèves de l'École Polytechnique ont marqué leur temps. On y trouvait de nombreuses notions nouvelles sur l'analyse réelle et complexe, et surtout une exigence de rigueur très novatrice pour l'époque. Le texte suivant est extrait du cours d'Analyse algébrique, écrit en 1821. Saurez-vous y reconnaître les notions de ce chapitre ?

On dit qu'une quantité variable devient infiniment petite, lorsque sa valeur numérique décroît indéfiniment, de manière à converger vers la limite zéro. Il est bon de remarquer à ce sujet qu'on ne doit pas confondre un décroissement constant avec un décroissement indéfini. La surface d'un polygone régulier circonscrit à un cercle donné décroît constamment à mesure que le nombre des côtés augmente, mais non pas indéfiniment, puisqu'elle a pour limite la surface du cercle. De même encore, une variable qui n'admettrait pour valeurs successives que les différents termes de la suite

$$\frac{2}{1} ,\;\frac{3}{2} ,\;\frac{4}{3} ,\; \frac{5}{4} ,\;\frac{6}{5} ,\ldots,$$

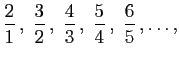
prolongée à l'infini, décroîtrait constamment, mais non pas indéfiniment, puisque ses valeurs successives convergeraient vers la limite $1$. Au contraire, une variable qui n'aurait pour valeurs successives que les différents termes de la suite

$$\frac{1}{4} ,\;\frac{1}{3} ,\;\frac{1}{6} ,\; \frac{1}{5} ,\;\frac{1}{8} ,\;\frac{1}{7} ,\ldots,$$

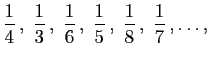
prolongée à l'infini, ne décroîtrait pas constamment, puisque la différence entre deux termes consécutifs de cette suite est alternativement positive et négative ; et, néanmoins, elle décroîtrait indéfiniment, puisque sa valeur finirait par s'abaisser au-dessous de tout nombre donné.

$$[\ldots]$$

Parmi les objets qui se rattachent à la considération des infiniment petits, on doit placer les notions relatives à la continuité ou à la discontinuité des fonctions. Examinons d'abord sous ce point de vue les fonctions d'une seule variable.

Soit $f(x)$ une fonction de la variable $x$, et supposons que, pour chaque valeur de $x$ intermédiaire entre deux limites données, cette fonction admette constamment une valeur unique et finie. Si, en partant d'une valeur de $x$ comprise entre ces limites, on attribue à la variable $x$ un accroissement infiniment petit $\alpha$, la fonction elle-même recevra pour accroissement la différence $f(x+\alpha)-f(x)$, qui dépendra en même temps de la nouvelle variable $\alpha$ et de la valeur de $x$. Cela posé, la fonction $f(x)$ sera, entre les deux limites assignées à la variable $x$, fonction continue de cette variable, si, pour chaque valeur de $x$ intermédiaire entre ces limites, la valeur numérique de la différence $f(x+\alpha)-f(x)$ décroît indéfiniment avec celle de $\alpha$.

En d'autres termes, la fonction $f(x)$ restera continue par rapport à $x$ entre les limites données, si, entre ces limites, un accroissement infiniment petit de la variable produit toujours un accroissement infiniment petit de la fonction elle-même.

On dit encore que la fonction $f(x)$ est, dans le voisinage d'une valeur particulière attribuée à la variable $x$, fonction continue de cette variable, toutes les fois qu'elle est continue entre deux limites de $x$, même très rapprochées, qui renferment la valeur dont il s'agit.

Enfin, lorsqu'une fonction $f(x)$ cesse d'être continue dans le voisinage d'une valeur particulière de la variable $x$, on dit qu'elle devient alors discontinue et qu'il y a pour cette valeur particulière une solution de continuité.