Définition 8
Soit 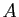 une partie de
une partie de
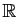 . On
dit que
. On
dit que 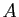 est dense dans
est dense dans
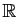 si tout réel est
limite d'une suite d'éléments de
si tout réel est
limite d'une suite d'éléments de 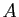 .
.
Une partie dense peut aussi être vue comme un ensemble de
réels tel que tout intervalle ouvert de
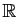 contient au moins un
élément de cet ensemble.
contient au moins un
élément de cet ensemble.
Proposition 8
Une partie 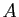 est dense dans
est dense dans
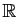 si et seulement si, pour tous
réels
si et seulement si, pour tous
réels 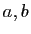 tels que
tels que 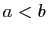 ,
,
![$ A\cap ]a,b[\neq \emptyset$](img757.gif) .
.
La démonstration est facile et
laissée au lecteur.
Le théorème suivant semble trop simple pour être utile, et
pourtant...
Théorème 15
Soit 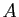 une partie dense de
une partie dense de
 .
Si deux fonctions continues sont égales sur
.
Si deux fonctions continues sont égales sur 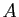 alors elles sont
égales partout.
alors elles sont
égales partout.
Démonstration : Soit  un réel et
un réel et 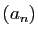 une suite d'éléments de
une suite d'éléments de 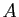 ,
convergeant vers
,
convergeant vers  . Comme
. Comme  et
et 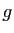 sont continues, les suites
sont continues, les suites
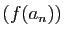 et
et 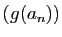 convergent respectivement vers
convergent respectivement vers 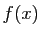 et
et
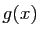 . Mais comme les deux suites sont égales, leurs limites sont
égales.
. Mais comme les deux suites sont égales, leurs limites sont
égales. 
Appliquer le théorème 15
se dit «utiliser un argument de continuité». Le plus souvent,
la partie dense est l'ensemble des rationnels
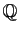 . On peut aussi
rencontrer l'ensemble des nombres décimaux (multiples entiers d'une
puissance négative de
. On peut aussi
rencontrer l'ensemble des nombres décimaux (multiples entiers d'une
puissance négative de 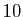 ), et l'ensemble des nombres
dyadiques (multiples entiers d'une
puissance négative de
), et l'ensemble des nombres
dyadiques (multiples entiers d'une
puissance négative de 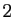 ).
).
Les quatre exemples de la proposition
9 proviennent du cours d'Analyse de Cauchy, chapitre V,
paragraphe 1 : «Recherche d'une fonction continue formée de telle
manière que deux semblables fonctions de quantités variables,
étant ajoutées ou multipliées entre elles, donnent pour somme ou
pour produit une fonction semblable de la somme ou du produit de ces
variables» (comment ça pas très clair ? Un peu de respect pour
Cauchy tout de même !)
Proposition 9
- Soit
 une fonction continue sur
une fonction continue sur
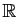 , telle que
, telle que
Alors, en notant 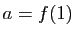 ,
,
- Soit
 une fonction continue sur
une fonction continue sur
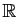 , telle que
, telle que
Alors, en notant 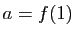 ,
,
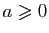 et
et
- Soit
 une fonction continue sur
une fonction continue sur
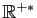 , telle que
, telle que
Il existe
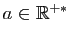 tel que
tel que 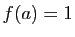 et :
et :
- Soit
 une fonction continue sur
une fonction continue sur
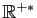 , telle que
, telle que
Alors, soit  est constamment nulle, soit
est constamment nulle, soit
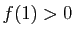 , et en notant
, et en notant
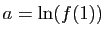 :
:
Démonstration : Nous détaillons la démonstration du premier point. Celle
des autres points se fait sur le même modèle et
sera laissée au lecteur.
Supposons que  vérifie
vérifie
Soit  un réel quelconque.
Commençons par montrer, par récurrence sur
un réel quelconque.
Commençons par montrer, par récurrence sur 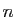 , que
pour tout
, que
pour tout
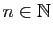 ,
,
La propriété est vraie pour 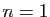 . Supposons qu'elle soit vraie
pour
. Supposons qu'elle soit vraie
pour 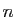 . Alors :
. Alors :
La propriété est vraie pour 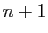 . Elle est donc vraie pour
tout
. Elle est donc vraie pour
tout
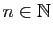 .
.
Soient 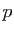 et
et 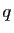 sont deux entiers. Appliquée à
sont deux entiers. Appliquée à 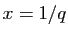 , la
propriété ci-dessus donne
, la
propriété ci-dessus donne
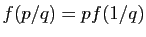 ,
et aussi
,
et aussi
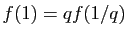 .
Donc
.
Donc
En posant 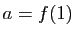 , la fonction
, la fonction  coïncide avec
coïncide avec
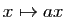 sur tous les rationnels positifs.
La relation
sur tous les rationnels positifs.
La relation
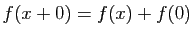 montre que
montre que 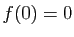 . En
écrivant
. En
écrivant
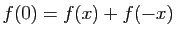 , on obtient que
, on obtient que
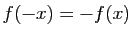 . La
fonction
. La
fonction  coïncide donc avec
coïncide donc avec
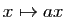 sur tous les
rationnels, donc sur tous les réels, par un argument de
continuité.
sur tous les
rationnels, donc sur tous les réels, par un argument de
continuité. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
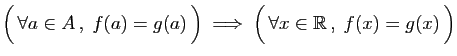
![]() . On peut aussi
rencontrer l'ensemble des nombres décimaux (multiples entiers d'une
puissance négative de
. On peut aussi
rencontrer l'ensemble des nombres décimaux (multiples entiers d'une
puissance négative de ![]() ), et l'ensemble des nombres
dyadiques (multiples entiers d'une
puissance négative de
), et l'ensemble des nombres
dyadiques (multiples entiers d'une
puissance négative de ![]() ).
).
![]() vérifie
vérifie
![]() et
et ![]() sont deux entiers. Appliquée à
sont deux entiers. Appliquée à ![]() , la
propriété ci-dessus donne
, la
propriété ci-dessus donne
![]() ,
et aussi
,
et aussi
![]() .
Donc
.
Donc
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales