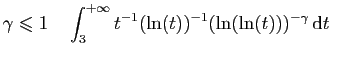 diverge,
diverge,
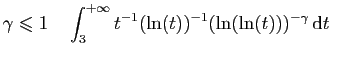 diverge,
diverge,
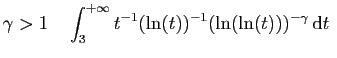 converge.
converge.
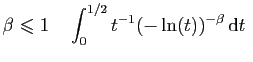 diverge,
diverge,
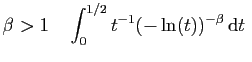 converge.
converge.
Dans les exemples suivants,
![]() désignent des
réels strictement positifs. Les intégrales suivantes sont
convergentes.
désignent des
réels strictement positifs. Les intégrales suivantes sont
convergentes.
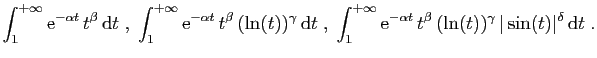
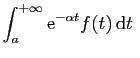 est absolument convergente.
est absolument convergente.
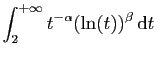 converge.
converge.
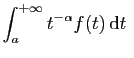 est absolument convergente.
est absolument convergente.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales