Nous traitons ici le cas où la fonction à intégrer tend vers
l'infini en l'une des bornes de l'intervalle d'intégration.
Le traitement est tout à fait analogue au cas précédent.
Quitte à réduire l'intervalle d'intégration, et à changer
éventuellement le signe de 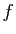 , nous pouvons supposer que la
fonction est positive ou nulle sur l'intervalle d'intégration
, nous pouvons supposer que la
fonction est positive ou nulle sur l'intervalle d'intégration
![$ ]a,b]$](img19.gif) , et tend vers
, et tend vers 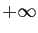 en
en 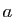 (figure 2).
(figure 2).
Figure 4:
Intégrale d'une fonction positive non bornée.
|
|
Rappelons que par définition,
Observons que si la fonction 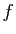 est positive, alors
est positive, alors
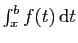 croît quand
croît quand 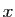 décroît vers
décroît vers 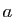 :
soit
:
soit
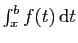 est bornée, et l'intégrale
est bornée, et l'intégrale
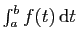 est convergente, soit
est convergente, soit
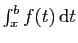 tend vers
tend vers
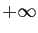 .
.
Si on ne peut pas (ou si on ne
veut pas) calculer une primitive de 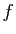 , on étudie la convergence en
comparant avec des intégrales dont la convergence est connue,
grâce au théorème suivant.
, on étudie la convergence en
comparant avec des intégrales dont la convergence est connue,
grâce au théorème suivant.
Démonstration : Comme nous l'avons observé, la convergence des intégrales ne
dépend pas de la borne de droite de l'intervalle, et nous pouvons
nous contenter d'étudier
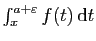 et
et
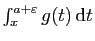 .
Or en utilisant la monotonie des intégrales, on obtient que pour
tout
.
Or en utilisant la monotonie des intégrales, on obtient que pour
tout
![$ x\in]a,a+\varepsilon]$](img123.gif) :
:
Si
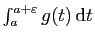 converge,
alors
converge,
alors
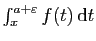 croît quand
croît quand 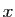 décroît vers
décroît vers 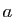 et est majorée par
et est majorée par
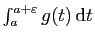 , elle converge donc.
Inversement, si
, elle converge donc.
Inversement, si
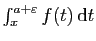 tend vers
tend vers
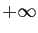 , alors
, alors
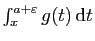 tend vers
tend vers 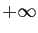 également.
également. Voici une application typique du théorème de comparaison des
intégrales 3. Nous allons montrer que
l'intégrale
Voici une application typique du théorème de comparaison des
intégrales 3. Nous allons montrer que
l'intégrale
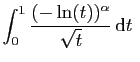
converge,
pour tout réel 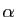 . Pour cela nous écrivons :
. Pour cela nous écrivons :
On sait que
pour tout 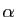 (les puissances de
(les puissances de
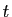 l'emportent sur le logarithme).
En particulier, il existe un réel
l'emportent sur le logarithme).
En particulier, il existe un réel
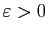 tel que :
tel que :
En multipliant les deux membres de l'inégalité
par 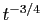 on obtient :
on obtient :
Or l'intégrale
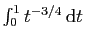 converge. En effet :
converge. En effet :
![$\displaystyle \int_x^1 t^{-3/4} \mathrm{d}t = \Big[4 t^{1/4}\Big]_x^1 =
4-4x^{1/4}$](img134.gif)
et
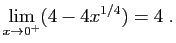
On peut donc appliquer le théorème de
comparaison 3 :
puisque
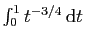 converge, on en déduit que
converge, on en déduit que
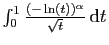 converge aussi.
Grâce au théorème de comparaison 3,
on peut remplacer la fonction
à intégrer par un équivalent au voisinage de
converge aussi.
Grâce au théorème de comparaison 3,
on peut remplacer la fonction
à intégrer par un équivalent au voisinage de 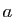 pour
étudier la convergence d'une intégrale.
pour
étudier la convergence d'une intégrale.
Démonstration : Dire que deux fonctions sont équivalentes au voisinage de 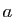 ,
c'est dire que le rapport tend vers
,
c'est dire que le rapport tend vers 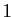 , ou encore :
, ou encore :
soit encore :
Fixons
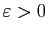 , et appliquons le théorème de comparaison
3 sur
l'intervalle
, et appliquons le théorème de comparaison
3 sur
l'intervalle
![$ ]a,a+\eta]$](img140.gif) . Si l'intégrale
. Si l'intégrale
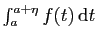 converge, alors l'intégrale
converge, alors l'intégrale
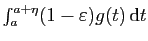 converge, donc l'intégrale
converge, donc l'intégrale
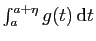 aussi par la linéarité (proposition
1). Inversement, si
aussi par la linéarité (proposition
1). Inversement, si
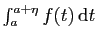 diverge, alors
diverge, alors
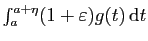 diverge, donc
diverge, donc
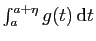 diverge aussi.
diverge aussi.  Par exemple, l'intégrale
Par exemple, l'intégrale
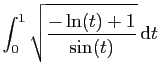
converge.
En effet,
et nous avons déjà montré que l'intégrale
 converge.
converge.
L'utilisation des équivalents permet ainsi de ramener l'étude de la
convergence d'une intégrale pour laquelle on n'a pas de primitive,
à un catalogue d'intégrales dont la convergence est connue. Les
plus classiques sont du type
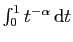 , mais
attention, la convergence en fonction du paramètre
, mais
attention, la convergence en fonction du paramètre 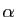 est
inversée par rapport aux intégrales de Riemann.
est
inversée par rapport aux intégrales de Riemann.
Si
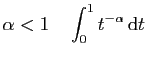
converge,
si
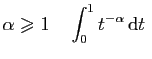
diverge.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() , nous pouvons supposer que la
fonction est positive ou nulle sur l'intervalle d'intégration
, nous pouvons supposer que la
fonction est positive ou nulle sur l'intervalle d'intégration
![]() , et tend vers
, et tend vers ![]() en
en ![]() (figure 2).
(figure 2).
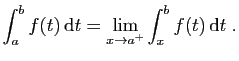
![]() , on étudie la convergence en
comparant avec des intégrales dont la convergence est connue,
grâce au théorème suivant.
, on étudie la convergence en
comparant avec des intégrales dont la convergence est connue,
grâce au théorème suivant.
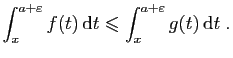
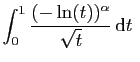 converge,
converge,
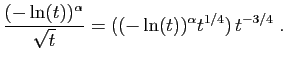
![$\displaystyle \forall t\in]0,\varepsilon] ,\; \frac{(-\ln(t))^\alpha}{\sqrt{t}}\leqslant t^{-3/4}\;.
$](img132.gif)
![$\displaystyle \int_x^1 t^{-3/4} \mathrm{d}t = \Big[4 t^{1/4}\Big]_x^1 =
4-4x^{1/4}$](img134.gif) et
et 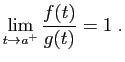
![$\displaystyle \forall \varepsilon>0 ,\;\exists \eta ,\; \forall t\in]a,a+\eta]\;,\quad
\left\vert\frac{f(t)}{g(t)}-1\right\vert<\varepsilon\;,
$](img138.gif)
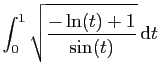 converge.
converge.
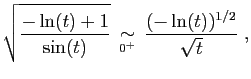
![]() , mais
attention, la convergence en fonction du paramètre
, mais
attention, la convergence en fonction du paramètre ![]() est
inversée par rapport aux intégrales de Riemann.
est
inversée par rapport aux intégrales de Riemann.
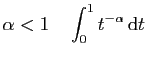 converge,
converge,
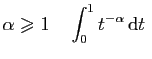 diverge.
diverge.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales