Le dernier cas à traiter est celui où la fonction à intégrer
oscille au voisinage d'une des bornes, prenant des valeurs
arbitrairement proches de 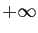 et
et 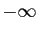 (figure 6).
(figure 6).
Figure 6:
Intégrale d'une fonction positive non bornée.
|
|
Le changement de variable 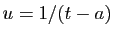 permet de se ramener au cas
précédent, ce qui nous dispensera de donner autant de détails.
Rappelons que par définition,
permet de se ramener au cas
précédent, ce qui nous dispensera de donner autant de détails.
Rappelons que par définition,
La notion importante est toujours la convergence absolue.
Définition 3
Soit 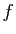 une fonction continue sur
une fonction continue sur ![$ ]a,b]$](img19.gif) . On dit que
. On dit que
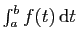 est absolument convergente si
est absolument convergente si
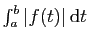 est une intégrale convergente.
est une intégrale convergente.
Nous admettrons le théorème suivant, qui se démontre de la
même façon que le théorème 5.
Théorème 7
Si l'intégrale
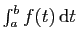 est absolument convergente,
alors elle est convergente.
est absolument convergente,
alors elle est convergente.
Par exemple,
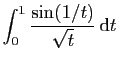
est absolument convergente,
donc convergente. En effet pour tout 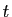 ,
,
Or l'intégrale
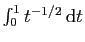 converge. D'où le résultat par le théorème de comparaison
3.
Par contre,
converge. D'où le résultat par le théorème de comparaison
3.
Par contre,
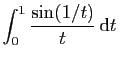
n'est pas absolument convergente,
mais elle est convergente.
Pour le voir, effectuons le changement de variable
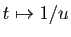 .
.
Nous avons déjà montré que l'intégrale
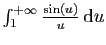 est convergente sans être
absolument convergente.
est convergente sans être
absolument convergente.
On pourrait énoncer un théorème d'Abel analogue au théorème
6, mais cela n'est pas vraiment utile. D'une part
les fonctions auxquelles il s'appliquerait se rencontrent rarement,
d'autre part, il est en général facile de se ramener à un
problème sur
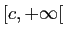 , par le changement de variable
, par le changement de variable
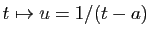 : nous l'avons déjà fait
pour
: nous l'avons déjà fait
pour
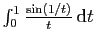 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
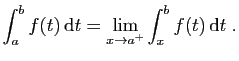
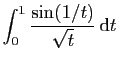 est absolument convergente,
est absolument convergente,
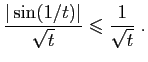
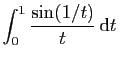 n'est pas absolument convergente,
n'est pas absolument convergente,
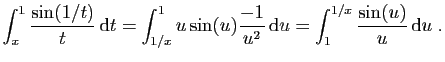
![]() , par le changement de variable
, par le changement de variable
![]() : nous l'avons déjà fait
pour
: nous l'avons déjà fait
pour
![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales