Nous considérons ici
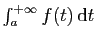 , où
, où 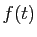 oscille jusqu'à l'infini entre des valeurs positives et négatives
(figure 5).
oscille jusqu'à l'infini entre des valeurs positives et négatives
(figure 5).
Figure 5:
Intégrale d'une fonction oscillante sur un intervalle non borné.
|
|
La définition de la convergence reste la même.
Contrairement au cas des fonctions positives, où la limite était
soit finie, soit égale à 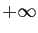 , tous les comportements sont
possibles ici : les valeurs de
, tous les comportements sont
possibles ici : les valeurs de
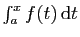 peuvent tendre vers
une limite finie, vers
peuvent tendre vers
une limite finie, vers 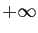 ou
ou 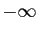 ou bien encore osciller
entre deux valeurs finies (comme
ou bien encore osciller
entre deux valeurs finies (comme
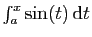 ), ou
s'approcher alternativement de
), ou
s'approcher alternativement de 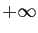 et
et 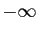 (comme
(comme
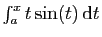 ).
).
Le cas le plus favorable est celui où la valeur absolue de 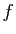 converge.
converge.
Définition 2
Soit  une fonction continue sur
une fonction continue sur
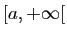 . On dit que
. On dit que
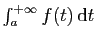 est absolument convergente si
est absolument convergente si
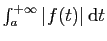 converge.
converge.
Le théorème suivant est souvent utilisé pour démontrer la
convergence d'une intégrale. Malheureusement, il ne permet pas de
calculer la valeur de cette intégrale.
Théorème 5
Si l'intégrale
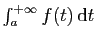 est absolument
convergente, alors elle est convergente.
est absolument
convergente, alors elle est convergente.
Démonstration : Rappelons la définition :
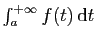 converge
si et seulement si
converge
si et seulement si
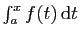 converge. Posons
converge. Posons
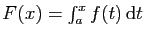 . Nous allons démontrer que, pour toute
suite
. Nous allons démontrer que, pour toute
suite
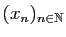 , tendant vers l'infini, la suite
, tendant vers l'infini, la suite
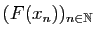 est une suite de Cauchy.
Sans perte de généralité, nous pouvons supposer que la suite
est une suite de Cauchy.
Sans perte de généralité, nous pouvons supposer que la suite
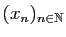 est strictement croissante. Par la relation de
Chasles, pour tout couple d'entiers
est strictement croissante. Par la relation de
Chasles, pour tout couple d'entiers 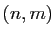 avec
avec 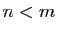 :
:
Or par hypothèse, l'intégrale
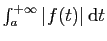 converge. On en déduit que
la suite de terme général
converge. On en déduit que
la suite de terme général
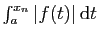 converge : c'est donc une suite de Cauchy. Pour tout
converge : c'est donc une suite de Cauchy. Pour tout
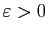 ,
il existe
,
il existe  tel que pour
tel que pour 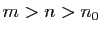 ,
,
La suite
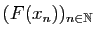 est une suite de Cauchy, donc elle
converge. Puisque c'est vrai pour toute suite
est une suite de Cauchy, donc elle
converge. Puisque c'est vrai pour toute suite
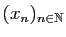 tendant vers l'infini, la fonction
tendant vers l'infini, la fonction
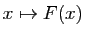 admet une limite en
admet une limite en
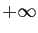 , d'où le résultat.
, d'où le résultat. Par exemple,
Par exemple,
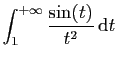
est absolument convergente,
donc convergente. En effet pour tout 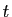 ,
,
Or l'intégrale de Riemann
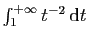 est
convergente. D'où le résultat par le théorème de comparaison
1.
Par contre,
est
convergente. D'où le résultat par le théorème de comparaison
1.
Par contre,
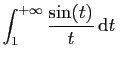
n'est pas absolument convergente.
Voici un moyen de le vérifier. Comme
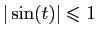 pour tout
pour tout
 , on a :
, on a :
En appliquant une intégration par parties à
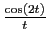 , on obtient :
, on obtient :
Or
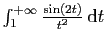 converge absolument, comme
nous venons de le voir. Des 3 termes de la somme ci-dessus, les deux
derniers convergent, le premier tend vers
converge absolument, comme
nous venons de le voir. Des 3 termes de la somme ci-dessus, les deux
derniers convergent, le premier tend vers 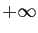 . Donc
l'intégrale diverge, et par le théorème de comparaison
1, l'intégrale
. Donc
l'intégrale diverge, et par le théorème de comparaison
1, l'intégrale
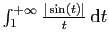 diverge également.
diverge également.
Il se trouve que
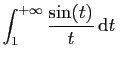
converge.
Pour le montrer, effectuons une intégration par parties :
La fonction
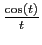 tend vers 0 (car
tend vers 0 (car 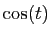 est
borné et
est
borné et
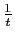 tend vers 0). Par comparaison avec
l'intégrale de Riemann
tend vers 0). Par comparaison avec
l'intégrale de Riemann
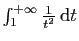 , on
montre que l'intégrale
, on
montre que l'intégrale
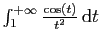 est absolument convergente, donc convergente. Par conséquent,
est absolument convergente, donc convergente. Par conséquent,
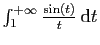 converge.
converge.
Pour montrer qu'une intégrale converge quand elle n'est pas
absolument convergente, on dispose du théorème suivant, dit
théorème d'Abel.
Démonstration : C'est une généralisation de l'exemple précédent.
Pour tout
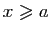 , posons
, posons
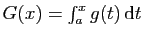 . Par
hypothèse,
. Par
hypothèse, 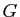 est bornée, donc il existe
est bornée, donc il existe 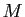 tel que pour tout
tel que pour tout 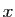 ,
,
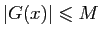 . Effectuons maintenant une intégration par parties.
. Effectuons maintenant une intégration par parties.
Comme 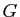 est bornée et
est bornée et 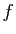 tend vers 0, le premier terme
converge. Montrons maintenant que le deuxième
converge aussi, en vérifiant que
tend vers 0, le premier terme
converge. Montrons maintenant que le deuxième
converge aussi, en vérifiant que
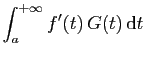
est absolument convergente.

On a :
car 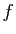 est décroissante (donc
est décroissante (donc
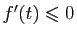 ) et
) et 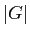 est bornée
par
est bornée
par 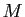 . Par le théorème de comparaison
1, il suffit donc de montrer que
. Par le théorème de comparaison
1, il suffit donc de montrer que
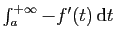 est convergente. Or :
est convergente. Or :
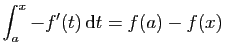
et
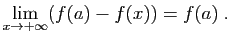
 Comme exemple d'application, si
Comme exemple d'application, si 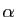 est un réel strictement
positif, et
est un réel strictement
positif, et 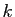 un entier positif impair, alors l'intégrale
un entier positif impair, alors l'intégrale
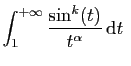
converge.
Remarquons que cette intégrale n'est absolument convergente que
pour 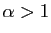 .
On vérifie que les hypothèses du théorème 6 sont
satisfaites pour
.
On vérifie que les hypothèses du théorème 6 sont
satisfaites pour
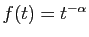 et
et
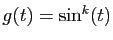 . Pour
s'assurer que la primitive de
. Pour
s'assurer que la primitive de 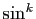 est bornée, il suffit de
penser à une linéarisation, qui transformera
est bornée, il suffit de
penser à une linéarisation, qui transformera 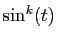 en une
combinaison linéaire des
en une
combinaison linéaire des
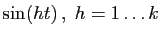 , dont la
primitive sera toujours bornée.
, dont la
primitive sera toujours bornée.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
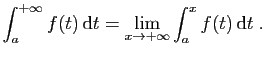
![]() converge.
converge.
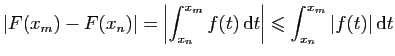
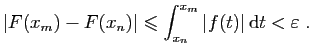
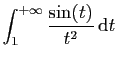 est absolument convergente,
est absolument convergente,
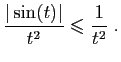
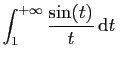 n'est pas absolument convergente.
n'est pas absolument convergente.
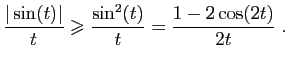
![$\displaystyle \int_1^x \frac{1-2\cos(2t)}{2t} \mathrm{d}t
= \frac{1}{2}\Big[\...
...sin(2t)}{t}\right]_1^x
+\frac{1}{2}\int_1^x \frac{\sin(2t)}{t^2} \mathrm{d}t.
$](img174.gif)
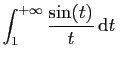 converge.
converge.
![$\displaystyle \int_1^x \frac{\sin(t)}{t} \mathrm{d}t = \left[\frac{-\cos(t)}{t}\right]_1^x
- \int_1^x \frac{\cos(t)}{t^2} \mathrm{d}t\;.
$](img177.gif)
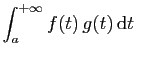 converge.
converge.
![$\displaystyle \int_a^x f(t) g(t) \mathrm{d}t = \Big[ f(t) G(t)\Big ]_a^x
-\int_a^x f'(t) G(t) \mathrm{d}t\;.
$](img191.gif)
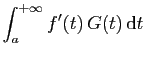 est absolument convergente.
est absolument convergente.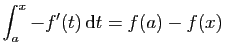 et
et 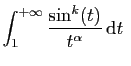 converge.
converge.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales