Notre but dans ce chapitre est de calculer des intégrales sur des
intervalles non bornés (allant jusqu'à 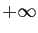 ou
ou 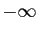 ), ou
bien des intégrales sur un domaine borné, de fonctions ayant une
limite infinie en un point de l'intervalle
d'intégration.
Si on se réfère à l'interprétation intuitive d'une
intégrale comme la surface d'un domaine dans le plan,
dans les deux cas nous cherchons
à calculer des surfaces de domaines non bornés.
), ou
bien des intégrales sur un domaine borné, de fonctions ayant une
limite infinie en un point de l'intervalle
d'intégration.
Si on se réfère à l'interprétation intuitive d'une
intégrale comme la surface d'un domaine dans le plan,
dans les deux cas nous cherchons
à calculer des surfaces de domaines non bornés.
Considérons par exemple la fonction 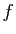 qui à
qui à
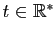 associe
associe
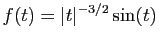 : son graphe est
représenté sur la figure 1.
: son graphe est
représenté sur la figure 1.
Figure:
Graphe de la fonction
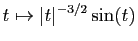 .
.
|
|
Comment donner un sens à l'intégrale de 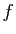 sur
sur
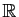 ?
Nous souhaitons une définition qui respecte les propriétés de
base que sont la
relation de Chasles, la linéarité et la monotonie.
?
Nous souhaitons une définition qui respecte les propriétés de
base que sont la
relation de Chasles, la linéarité et la monotonie.
On commence d'abord par identifier les points incertains, soit
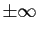 d'une part, et d'autre part le ou les points au voisinage
desquels la fonction n'est pas bornée (
d'une part, et d'autre part le ou les points au voisinage
desquels la fonction n'est pas bornée (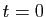 dans notre exemple). On
découpe ensuite l'intervalle d'intégration en autant d'intervalles
qui faut pour que chacun d'eux ne contienne qu'un seul point
incertain, placé à l'une des deux bornes. La relation de Chasles
impose que l'intégrale sur l'intervalle complet soit la somme des
intégrales sur les intervalles du découpage. Dans l'exemple de la
fonction
dans notre exemple). On
découpe ensuite l'intervalle d'intégration en autant d'intervalles
qui faut pour que chacun d'eux ne contienne qu'un seul point
incertain, placé à l'une des deux bornes. La relation de Chasles
impose que l'intégrale sur l'intervalle complet soit la somme des
intégrales sur les intervalles du découpage. Dans l'exemple de la
fonction
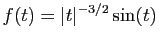 ci-dessus,
il faut découper en 4 sous-intervalles : 2 pour isoler
ci-dessus,
il faut découper en 4 sous-intervalles : 2 pour isoler
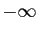 et
et 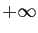 , et 2 autres pour le point incertain 0. On
pourra écrire par exemple :
, et 2 autres pour le point incertain 0. On
pourra écrire par exemple :
Le seul but est d'isoler les difficultés : les choix de 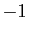 et
et 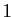 comme points de découpage sont arbitraires (par exemple
comme points de découpage sont arbitraires (par exemple 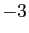 et
et 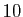 auraient
convenu tout aussi bien).
Par ce découpage, on se ramène à des intégrales de 4
types.
auraient
convenu tout aussi bien).
Par ce découpage, on se ramène à des intégrales de 4
types.
- intégrale sur
![$ ]-\infty,a]$](img17.gif) ,
,
- intégrale sur
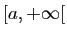 ,
,
- intégrale sur
![$ ]a,b]$](img19.gif) , fonction non bornée en
, fonction non bornée en 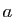 ,
,
- intégrale sur
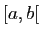 , fonction non bornée en
, fonction non bornée en 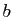 ,
,
Le changement de variable
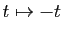 permet de réduire ces 4 cas à 2 seulement. En effet :
permet de réduire ces 4 cas à 2 seulement. En effet :
Nous devons donc définir l'intégrale dans deux cas distincts.
Observons que la deuxième définition est cohérente avec les
propriétés de l'intégrale d'une fonction continue :
si la fonction 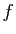 est
continue sur
est
continue sur ![$ [a,b]$](img33.gif) tout entier, alors
tout entier, alors
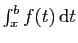 est une
fonction de
est une
fonction de 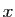 continue en
continue en 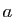 , et (2) est vérifié.
, et (2) est vérifié.
Dans
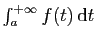 ,
la borne de gauche de l'intervalle d'intégration n'a pas d'influence
sur le comportement de l'intégrale. Supposons
,
la borne de gauche de l'intervalle d'intégration n'a pas d'influence
sur le comportement de l'intégrale. Supposons 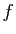 continue sur
continue sur
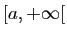 et choisissons un réel
et choisissons un réel
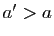 . Par la relation de Chasles,
. Par la relation de Chasles,
Comme
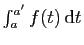 ne dépend pas de
ne dépend pas de 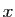 , la limite de
, la limite de
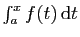 existe si et seulement si celle de
existe si et seulement si celle de
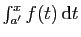 existe aussi. La convergence d'une intégrale ne dépend
donc pas du comportement de la fonction sur des intervalles bornés,
mais seulement de son comportement au voisinage de
existe aussi. La convergence d'une intégrale ne dépend
donc pas du comportement de la fonction sur des intervalles bornés,
mais seulement de son comportement au voisinage de 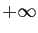 .
.
Si 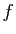 n'est pas bornée au voisinage de
n'est pas bornée au voisinage de 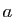 , la convergence de
, la convergence de
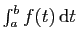 ne dépend pas de
ne dépend pas de 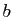 , pour la même raison :
elle ne dépend que du comportement de
, pour la même raison :
elle ne dépend que du comportement de 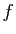 au voisinage de
au voisinage de 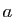 .
.
Le résultat suivant est une conséquence immédiate de la
linéarité des intégrales et des limites.
Quand on peut calculer une primitive de la fonction à intégrer,
l'étude de la convergence se ramène à un calcul de limite. Voici
plusieurs exemples.
L'intégrale
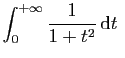
converge.
En effet,
![$\displaystyle \int_0^{x} \frac{1}{1+t^2} \mathrm{d}t =\Big[\arctan(t)\Big]_0^x
=\arctan(x)$](img49.gif)
et
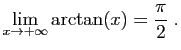
On pourra écrire :
à condition de se souvenir que
![$ \Big[\arctan(t)\Big]_0^{+\infty}$](img52.gif) désigne une limite en
désigne une limite en 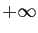 .
Par contre, l'intégrale
.
Par contre, l'intégrale
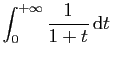
diverge.
En effet,
![$\displaystyle \int_0^{x} \frac{1}{1+t} \mathrm{d}t = \Big[\ln(1+t)\Big]_0^x
=\ln(1+x)$](img54.gif)
et
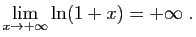
L'intégrale
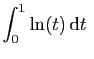
converge.
En effet,
![$\displaystyle \int_x^1 \ln(t) \mathrm{d}t = \Big[t\ln(t)-t\Big]_x^1 = x-x\ln(x)-1$](img57.gif)
et
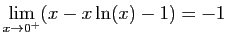
On pourra écrire :
Par contre, l'intégrale
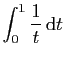
diverge.
En effet,
![$\displaystyle \int_x^1 \frac{1}{t} \mathrm{d}t = \Big[\ln(t)\Big]_x^1 = -\ln(x)$](img61.gif)
et
Figure 2:
Différents types d'intégrales :
(a) intervalle non borné, fonction de signe constant ;
(b) intervalle borné, fonction de signe constant ;
(c) intervalle non borné, fonction de signe non constant ;
(d) intervalle borné, fonction de signe non constant.
|
|
Quand on ne sait pas calculer une primitive, on a
recours à deux types de méthodes, selon que la fonction est ou non
de signe constant au voisinage du point incertain. Il y a donc 4 cas
distincts, selon le type du point incertain, et le signe, constant ou
non, de la fonction à intégrer. Ces 4 types sont schématisés
dans la figure 2 et leur étude fait
l'objet des sections suivantes.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() qui à
qui à
![]() associe
associe
![]() : son graphe est
représenté sur la figure 1.
: son graphe est
représenté sur la figure 1.
![]() d'une part, et d'autre part le ou les points au voisinage
desquels la fonction n'est pas bornée (
d'une part, et d'autre part le ou les points au voisinage
desquels la fonction n'est pas bornée (![]() dans notre exemple). On
découpe ensuite l'intervalle d'intégration en autant d'intervalles
qui faut pour que chacun d'eux ne contienne qu'un seul point
incertain, placé à l'une des deux bornes. La relation de Chasles
impose que l'intégrale sur l'intervalle complet soit la somme des
intégrales sur les intervalles du découpage. Dans l'exemple de la
fonction
dans notre exemple). On
découpe ensuite l'intervalle d'intégration en autant d'intervalles
qui faut pour que chacun d'eux ne contienne qu'un seul point
incertain, placé à l'une des deux bornes. La relation de Chasles
impose que l'intégrale sur l'intervalle complet soit la somme des
intégrales sur les intervalles du découpage. Dans l'exemple de la
fonction
![]() ci-dessus,
il faut découper en 4 sous-intervalles : 2 pour isoler
ci-dessus,
il faut découper en 4 sous-intervalles : 2 pour isoler
![]() et
et ![]() , et 2 autres pour le point incertain 0. On
pourra écrire par exemple :
, et 2 autres pour le point incertain 0. On
pourra écrire par exemple :
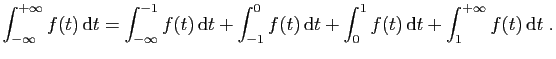
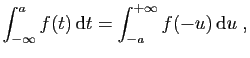
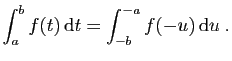
![]() ,
la borne de gauche de l'intervalle d'intégration n'a pas d'influence
sur le comportement de l'intégrale. Supposons
,
la borne de gauche de l'intervalle d'intégration n'a pas d'influence
sur le comportement de l'intégrale. Supposons ![]() continue sur
continue sur
![]() et choisissons un réel
et choisissons un réel
![]() . Par la relation de Chasles,
. Par la relation de Chasles,
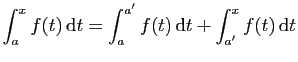
![]() n'est pas bornée au voisinage de
n'est pas bornée au voisinage de ![]() , la convergence de
, la convergence de
![]() ne dépend pas de
ne dépend pas de ![]() , pour la même raison :
elle ne dépend que du comportement de
, pour la même raison :
elle ne dépend que du comportement de ![]() au voisinage de
au voisinage de ![]() .
.
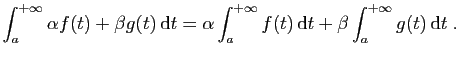
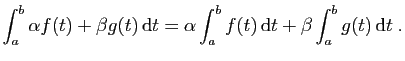
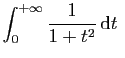 converge.
converge.
![$\displaystyle \int_0^{x} \frac{1}{1+t^2} \mathrm{d}t =\Big[\arctan(t)\Big]_0^x
=\arctan(x)$](img49.gif) et
et 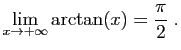
![$\displaystyle \int_0^{+\infty} \frac{1}{1+t^2} \mathrm{d}t = \Big[\arctan(t)\Big]_0^{+\infty}
=\frac{\pi}{2}\;,
$](img51.gif)
![$ \Big[\arctan(t)\Big]_0^{+\infty}$](img52.gif) désigne une limite en
désigne une limite en 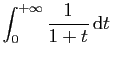 diverge.
diverge.
![$\displaystyle \int_0^{x} \frac{1}{1+t} \mathrm{d}t = \Big[\ln(1+t)\Big]_0^x
=\ln(1+x)$](img54.gif) et
et 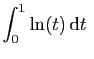 converge.
converge.
![$\displaystyle \int_x^1 \ln(t) \mathrm{d}t = \Big[t\ln(t)-t\Big]_x^1 = x-x\ln(x)-1$](img57.gif) et
et ![$\displaystyle \int_0^1 \ln(t) \mathrm{d}t = \Big[t\ln(t)-t\Big]_0^1 = -1\;.
$](img59.gif)
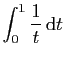 diverge.
diverge.
![$\displaystyle \int_x^1 \frac{1}{t} \mathrm{d}t = \Big[\ln(t)\Big]_x^1 = -\ln(x)$](img61.gif) et
et  © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales