Généralités
Une isométrie est clairement injective, puisque ![]() implique
implique
![]() et donc
et donc ![]() . Elle est bijective si
. Elle est bijective si ![]() et
et ![]() ont même dimension, en particulier si
ont même dimension, en particulier si ![]() , ce qui sera presque toujours ici le cas, mais cela ne se voit pas immédiatement sur la définition. Cela résultera en fait de la proposition fondamentale suivante :
, ce qui sera presque toujours ici le cas, mais cela ne se voit pas immédiatement sur la définition. Cela résultera en fait de la proposition fondamentale suivante :
Démonstration : Soit ![]() un point de
un point de ![]() et
et ![]() l'application de
l'application de
![]() dans
dans
![]() définie par
définie par
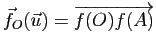 pour tout vecteur
pour tout vecteur ![]() de
de
![]() , où
, où ![]() est l'unique point de
est l'unique point de ![]() tel que
tel que
![]() . Si
. Si ![]() et
et ![]() sont deux vecteurs de
sont deux vecteurs de
![]() et
et ![]() et
et ![]() les points de
les points de ![]() tels que
tels que
![]() ,
,
![]() , on a :
, on a :
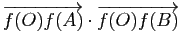 |
|||
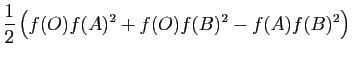 |
|||
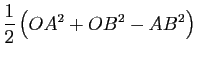 |
|||
Nous nous intéresserons essentiellement ici aux isométries d'un espace affine euclidien ![]() dans lui-même.
dans lui-même.
Démonstration : L'égalité
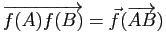 montre que
montre que
![]() pour tout couple
pour tout couple ![]() de points de
de points de ![]() si et seulement si
si et seulement si
![]() pour tout couple
pour tout couple ![]() de points de
de points de ![]() , ou encore si et seulement si
, ou encore si et seulement si
![]() pour tout vecteur
pour tout vecteur ![]() de
de
![]() .
.![]()
Démonstration : Cet ensemble est l'image réciproque du groupe orthogonal ![]() de
de
![]() par l'homomorphisme de groupes de
par l'homomorphisme de groupes de ![]() dans
dans ![]() qui à toute transformation affine
qui à toute transformation affine ![]() de
de ![]() associe sa partie linéaire
associe sa partie linéaire ![]() .
.![]()
Une isométrie ![]() de
de ![]() est dite indirecte ou négative si sa partie linéaire
est dite indirecte ou négative si sa partie linéaire ![]() est une transformation orthogonale négative de
est une transformation orthogonale négative de
![]() :
:
![]() . On dit aussi que
. On dit aussi que ![]() est un antidéplacement.
est un antidéplacement.
Les déplacements constituent un sous-groupe ![]() du groupe des isométries de
du groupe des isométries de ![]() . On note
. On note ![]() l'ensemble des antidéplacements de
l'ensemble des antidéplacements de ![]() (
(![]() n'est pas un groupe : le composé de deux antidéplacements est un déplacement).
n'est pas un groupe : le composé de deux antidéplacements est un déplacement).
Décomposition en produit de réflexions
On rappelle que l'ensemble, noté ![]() , des points fixes d'une transformation affine
, des points fixes d'une transformation affine ![]() d'un espace affine
d'un espace affine ![]() est soit vide, soit un sous-espace affine de
est soit vide, soit un sous-espace affine de ![]() .
.
Démonstration : La première assertion résulte de la proposition 16 . Pour démontrer la seconde, il suffit de remarquer que la matrice de la partie linéaire de la réflexion d'hyperplan ![]() dans une base orthonormée dont le premier vecteur est orthogonal à
dans une base orthonormée dont le premier vecteur est orthogonal à ![]() est diagonale, de diagonale
est diagonale, de diagonale
![]() .
. ![]()
(Si ![]() n'a pas de point fixe, il faut comprendre que
n'a pas de point fixe, il faut comprendre que ![]() a au moins un point fixe.)
a au moins un point fixe.)
Démonstration : Soit ![]() un point de
un point de ![]() tel que
tel que
![]() et
et ![]() la réflexion par rapport à l'hyperplan médiateur
la réflexion par rapport à l'hyperplan médiateur ![]() de
de ![]() . Tout point fixe
. Tout point fixe ![]() de
de ![]() appartient à
appartient à ![]() , puisque
, puisque
![]() , et est donc fixe par
, et est donc fixe par ![]() . Comme
. Comme ![]() n'appartient pas à
n'appartient pas à ![]() et est fixe par
et est fixe par ![]() ,
,
![]() est un sous-espace affine de
est un sous-espace affine de ![]() contenant strictement
contenant strictement ![]() .
.![]()
On en déduit par récurrence sur la dimension du sous-espace des points fixes, que les réflexions engendrent le groupe des isométries. Plus précisément :
Démonstration : Supposons ![]() fixé et démontrons le théorème par récurrence descendante sur
fixé et démontrons le théorème par récurrence descendante sur ![]() . Si
. Si ![]() ,
, ![]() et
et ![]() . Soit
. Soit
![]() un entier et
un entier et ![]() une isométrie telle que
une isométrie telle que
![]() . Alors il existe une réflexion
. Alors il existe une réflexion ![]() telle que
telle que
![]() . Si la propriété est vraie pour tout entier
. Si la propriété est vraie pour tout entier ![]() vérifiant
vérifiant
![]() ,
,
![]() peut s'écrire comme produit de
peut s'écrire comme produit de ![]() réflexions, avec
réflexions, avec
![]() ;
;
![]() s'écrit donc comme produit de
s'écrit donc comme produit de ![]() réflexions et
réflexions et
![]() .
.![]()
Cette décomposition n'est pas unique, mais la parité du nombre ![]() de réflexions y intervenant l'est, puisque le déterminant de
de réflexions y intervenant l'est, puisque le déterminant de ![]() est
est ![]() .
.
Classification des isométries planes
On suppose ici que ![]() est un plan affine euclidien et on se propose de préciser la nature géométrique des isométries.
est un plan affine euclidien et on se propose de préciser la nature géométrique des isométries.
Déplacements
Le cas des déplacements est simple : si ![]() est un déplacement du plan, sa partie linéaire
est un déplacement du plan, sa partie linéaire ![]() est soit l'identité, auquel cas
est soit l'identité, auquel cas ![]() est une translation, soit une rotation vectorielle d'angle non nul
est une translation, soit une rotation vectorielle d'angle non nul ![]() . Dans ce cas,
. Dans ce cas, ![]() possède un point fixe
possède un point fixe ![]() et un seul, puisque +1 n'est pas valeur propre de
et un seul, puisque +1 n'est pas valeur propre de ![]() . On dit que
. On dit que ![]() est la rotation de centre
est la rotation de centre ![]() et d'angle
et d'angle ![]() . L'image
. L'image ![]() d'un point
d'un point ![]() est caractérisée par les relations
est caractérisée par les relations ![]() ,
,
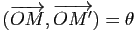 (modulo
(modulo ![]() ). On a donc démontré :
). On a donc démontré :
On en déduit que :
Antidéplacements
![\includegraphics[width=6cm]{symetries}](img748.gif)
Démonstration : Deux réflexions d'axes parallèles ont même partie linéaire, qui est une réflexion vectorielle. Leur produit est donc une transformation affine de partie linéaire l'identité, i.e. une translation. Pour trouver le vecteur de cette translation, il suffit de connaître l'image d'un point. Soit donc ![]() et
et ![]() deux réflexions d'axes parallèles
deux réflexions d'axes parallèles ![]() et
et ![]() ,
, ![]() une droite perpendiculaire à
une droite perpendiculaire à ![]() et
et ![]() les coupant respectivement en
les coupant respectivement en ![]() et
et ![]() . Le point
. Le point
![]() est le symétrique de
est le symétrique de ![]() par rapport à
par rapport à ![]() et vérifie donc
et vérifie donc
![]() . Il en résulte que
. Il en résulte que
![]() est la translation de vecteur
est la translation de vecteur
![]() . La réciproque est immédiate (on peut choisir l'un des deux points
. La réciproque est immédiate (on peut choisir l'un des deux points ![]() et
et ![]() arbitrairement, l'autre est alors uniquement déterminé).
arbitrairement, l'autre est alors uniquement déterminé).![]()
La partie linéaire ![]() d'un antidéplacement
d'un antidéplacement ![]() est une réflexion vectorielle. Soit
est une réflexion vectorielle. Soit ![]() son axe.
son axe.
Si ![]() admet un point fixe
admet un point fixe ![]() ,
, ![]() est la réflexion vectorielle d'axe la droite
est la réflexion vectorielle d'axe la droite ![]() de direction
de direction ![]() passant par
passant par ![]() .
.
Sinon, il existe un vecteur ![]() tel que
tel que
![]() admette un point fixe et soit donc une réflexion
admette un point fixe et soit donc une réflexion ![]() d'axe
d'axe ![]() . On décompose le vecteur
. On décompose le vecteur ![]() sous la forme
sous la forme ![]() , où
, où
![]() et
et ![]() est orthogonal à
est orthogonal à ![]() . On a alors
. On a alors
![]() . On peut alors (lemme 6) décomposer
. On peut alors (lemme 6) décomposer ![]() sous la forme
sous la forme
![]() , où
, où ![]() est une droite parallèle à
est une droite parallèle à ![]() . Il en résulte
. Il en résulte
![]() où
où
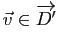 .
.
Ce produit est commutatif :
![]() . Une symétrie glissée n'admet pas de point fixe. L'axe et le vecteur d'une symétrie glissée
. Une symétrie glissée n'admet pas de point fixe. L'axe et le vecteur d'une symétrie glissée ![]() sont entièrement déterminés : en effet l'axe peut être caractérisé comme :
sont entièrement déterminés : en effet l'axe peut être caractérisé comme :
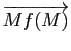 appartienne à l'axe de
appartienne à l'axe de
On a donc démontré :
![\includegraphics[width=6cm]{symetrieglissee}](img769.gif)
| Invariants | dépl/antidépl | nature géométrique |
| plan | déplacement | identité |
| droite | antidéplacement | réflexion |
| point | déplacement | rotation |
| déplacement | translation | |
| antidéplacement | symétrie glissée | |
| Classification des isométries planes | ||
Classification des isométries de l'espace
Déplacements
Soit ![]() un déplacement de l'espace affine euclidien
un déplacement de l'espace affine euclidien ![]() de dimension 3. Sa partie linéaire
de dimension 3. Sa partie linéaire ![]() est soit l'identité, soit une rotation vectorielle. Si
est soit l'identité, soit une rotation vectorielle. Si ![]() est l'identité,
est l'identité, ![]() est une translation.
Si
est une translation.
Si ![]() est une rotation vectorielle d'axe
est une rotation vectorielle d'axe ![]() et d'angle
et d'angle ![]() , deux cas se présentent :
, deux cas se présentent :
- soit ![]() a un point fixe
a un point fixe ![]() : dans ce cas
: dans ce cas ![]() est une rotation d'axe
est une rotation d'axe ![]() et d'angle
et d'angle ![]() , où
, où ![]() est la droite affine de direction
est la droite affine de direction ![]() passant par
passant par ![]() (
(![]() laisse globalement invariant tout plan
laisse globalement invariant tout plan ![]() orthogonal à
orthogonal à ![]() et sa restriction à un tel plan est une rotation de centre le point d'intersection de
et sa restriction à un tel plan est une rotation de centre le point d'intersection de ![]() et de
et de ![]() et d'angle
et d'angle ![]() ) ;
) ;
- soit ![]() n'a pas de point fixe ; il existe alors un vecteur
n'a pas de point fixe ; il existe alors un vecteur ![]() tel que
tel que
![]() admette un point fixe et soit donc une rotation
admette un point fixe et soit donc une rotation ![]() d'axe
d'axe ![]() ; on décompose le vecteur
; on décompose le vecteur ![]() sous la forme
sous la forme ![]() , où
, où
![]() et
et ![]() est orthogonal à
est orthogonal à ![]() ; on a alors
; on a alors
![]() ; mais
; mais
![]() laisse globalement invariant tout plan orthogonal à
laisse globalement invariant tout plan orthogonal à ![]() et sa restriction à un tel plan est une rotation plane d'angle
et sa restriction à un tel plan est une rotation plane d'angle ![]() (composée d'une translation et d'une rotation plane) ; soit
(composée d'une translation et d'une rotation plane) ; soit ![]() la droite parallèle à
la droite parallèle à ![]() passant par le centre d'une de ces rotations ;
passant par le centre d'une de ces rotations ;
![]() est alors la rotation de
est alors la rotation de ![]() d'axe
d'axe ![]() et d'angle
et d'angle ![]() ; il en résulte que
; il en résulte que ![]() est produit d'une rotation et d'une translation de vecteur un vecteur directeur de l'axe de la rotation ; ce produit est commutatif.
est produit d'une rotation et d'une translation de vecteur un vecteur directeur de l'axe de la rotation ; ce produit est commutatif.
On vérifie que cette décomposition est unique. L'axe ![]() peut être caractérisé comme :
peut être caractérisé comme :
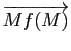 appartienne à l'axe de la rotation vectorielle
appartienne à l'axe de la rotation vectorielle
Un demi-tour est donc simplement une symétrie orthogonale par rapport à une droite. Les retournements sont les seuls déplacements involutifs. Leur importance vient en particulier du fait qu'ils engendrent le groupe des déplacements, comme le montre la proposition suivante.
Antidéplacements
La partie linéaire ![]() d'un antidéplacement
d'un antidéplacement ![]() est soit une réflexion vectorielle, soit une antirotation vectorielle (isométrie vectorielle gauche). Si
est soit une réflexion vectorielle, soit une antirotation vectorielle (isométrie vectorielle gauche). Si ![]() est une réflexion vectorielle, on montre comme dans le cas des antidéplacements du plan que
est une réflexion vectorielle, on montre comme dans le cas des antidéplacements du plan que ![]() est soit une réflexion, soit une symétrie glissée (produit commutatif d'une réflexion et d'une translation de vecteur appartenant à la direction du plan de la réflexion). Si
est soit une réflexion, soit une symétrie glissée (produit commutatif d'une réflexion et d'une translation de vecteur appartenant à la direction du plan de la réflexion). Si ![]() est une antirotation, 1 n'est pas valeur propre de
est une antirotation, 1 n'est pas valeur propre de ![]() ; il en résulte que
; il en résulte que ![]() admet un point fixe et un seul ;
admet un point fixe et un seul ; ![]() est donc encore une antirotation (produit commutatif d'une rotation et d'une réflexion de plan orthogonal à l'axe de la rotation).
est donc encore une antirotation (produit commutatif d'une rotation et d'une réflexion de plan orthogonal à l'axe de la rotation).
| Invariants | dépl/antidépl | nature géométrique |
| espace | déplacement | identité |
| plan | antidéplacement | réflexion |
| droite | déplacement | rotation |
| point | antidéplacement | antirotation |
| déplacement | vissage ou translation | |
| antidéplacement | symétrie glissée | |
| Classification des isométries de l'espace | ||
Groupe d'isométries conservant une figure
Démonstration : L'ensemble ![]() contient l'identité, est stable par composition et par passage à l'inverse ; c'est donc un sous-groupe du groupe
contient l'identité, est stable par composition et par passage à l'inverse ; c'est donc un sous-groupe du groupe ![]() . L'ensemble
. L'ensemble ![]() est l'intersection des sous-groupes
est l'intersection des sous-groupes ![]() et
et ![]() de
de ![]() ; c'est donc un sous-groupe de
; c'est donc un sous-groupe de ![]() . Si
. Si ![]() n'est pas vide, pour tout
n'est pas vide, pour tout ![]() , l'application
, l'application
![]() est une bijection de
est une bijection de ![]() sur
sur ![]() de bijection réciproque
de bijection réciproque
![]() .
.![]()
Remarque :
L'ensemble des isométries ![]() de
de ![]() qui vérifient
qui vérifient
![]() est stable par composition, mais n'est pas nécessairement un sous-groupe de
est stable par composition, mais n'est pas nécessairement un sous-groupe de ![]() (si
(si ![]() est une demi-droite de vecteur directeur
est une demi-droite de vecteur directeur ![]() , la translation de vecteur
, la translation de vecteur ![]() conserve
conserve ![]() , mais pas celle de vecteur
, mais pas celle de vecteur ![]() ). C'est toutefois le cas si
). C'est toutefois le cas si ![]() est fini, puisque dans ce cas
est fini, puisque dans ce cas ![]() pour toute isométrie
pour toute isométrie ![]() vérifiant
vérifiant
![]() , ou si
, ou si ![]() est un sous-espace affine, puisque dans ce cas
est un sous-espace affine, puisque dans ce cas ![]() est un sous-espace affine inclus dans
est un sous-espace affine inclus dans ![]() et de même dimension que
et de même dimension que ![]() , donc égal à
, donc égal à ![]() .
.
Démonstration : Une isométrie est une application affine et toute application affine conserve les barycentres. Il en résulte que l'isobarycentre ![]() de
de ![]() est fixe par toute isométrie conservant
est fixe par toute isométrie conservant ![]() . L'application
. L'application
![]() est un isomorphisme du groupe des isométries de
est un isomorphisme du groupe des isométries de ![]() laissant
laissant ![]() fixe sur le groupe orthogonal de
fixe sur le groupe orthogonal de
![]() ;
; ![]() est donc isomorphe à son image par cet homomorphisme, qui est un sous-groupe de
est donc isomorphe à son image par cet homomorphisme, qui est un sous-groupe de ![]() .
.![]()
Exemple : le groupe diédral ![]()
C'est le groupe des isométries planes conservant un polygone régulier convexe
![]() à
à ![]() côtés.
Son sous-groupe des déplacements
côtés.
Son sous-groupe des déplacements ![]() est le groupe cyclique d'ordre
est le groupe cyclique d'ordre ![]() constitué des
constitué des ![]() rotations de centre le centre
rotations de centre le centre ![]() du polygone et d'angle
du polygone et d'angle ![]() (
(
![]() ). Les éléments de
). Les éléments de ![]() sont les
sont les ![]() réflexions d'axes les droites
réflexions d'axes les droites ![]() (
(
![]() ) et les médiatrices des côtés du polygone (ces deux familles étant confondues si
) et les médiatrices des côtés du polygone (ces deux familles étant confondues si ![]() est impair et ayant chacune
est impair et ayant chacune ![]() éléments si
éléments si ![]() est pair).
est pair).
Remarque : Une isométrie qui conserve globalement l'ensemble des sommets d'un polygone régulier conserve ce polygone (et réciproquement). Il ne faut pas croire que cette propriété s'étend à tout polygone, comme en témoigne la figure ci-dessous : les rotations de centre ![]() et d'angle
et d'angle
![]() conservent les sommets du polygone
conservent les sommets du polygone ![]() mais pas ce polygone.
mais pas ce polygone.
![\includegraphics[width=0.4\textwidth]{polygone}](img795.gif)
Similitudes
Une application ![]() de
de ![]() dans
dans ![]() est donc une similitude si et seulement si elle conserve les rapports de distances.
est donc une similitude si et seulement si elle conserve les rapports de distances.
Une similitude de rapport 1 est une isométrie. Une homothétie de rapport ![]() est une similitude de rapport
est une similitude de rapport ![]() .
.
Démonstration : Soit ![]() une similitude de rapport
une similitude de rapport ![]() et
et ![]() une homothétie de rapport
une homothétie de rapport ![]() (et de centre quelconque). Alors
(et de centre quelconque). Alors ![]() est une transformation affine de
est une transformation affine de ![]() d'inverse l'homothétie
d'inverse l'homothétie ![]() de même centre et de rapport
de même centre et de rapport ![]() et
et
![]() est une isométrie, puisque
est une isométrie, puisque
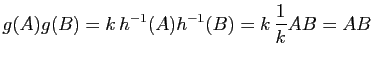
Deux figures sont dites semblables (resp. directement semblables) s'il existe une similitude (resp. une similitude directe) transformant la première en la seconde.
Démonstration : Soit ![]() une similitude de rapport
une similitude de rapport ![]() différent de 1. Il suffit de montrer que 1 n'est pas valeur propre de
différent de 1. Il suffit de montrer que 1 n'est pas valeur propre de ![]() (voir le chapitre «Géométrie affine »). Mais si
(voir le chapitre «Géométrie affine »). Mais si ![]() est un vecteur de
est un vecteur de
![]() , l'égalité
, l'égalité ![]() implique
implique
![]() , d'où
, d'où ![]() et
et ![]() .
.![]()
Similitudes planes
Une similitude directe qui n'est pas une isométrie est donc caractérisée par son centre (son seul point fixe), son rapport et son angle (l'angle de la rotation de la décomposition précédente).
Démonstration : Soit ![]() une similitude plane directe de rapport
une similitude plane directe de rapport ![]() différent de 1. D'après la proposition 63,
différent de 1. D'après la proposition 63, ![]() admet un point fixe
admet un point fixe ![]() et un seul. Soit
et un seul. Soit ![]() l'homothétie de centre
l'homothétie de centre ![]() et de rapport
et de rapport ![]() . La transformation affine
. La transformation affine
![]() est une isométrie directe laissant fixe le point
est une isométrie directe laissant fixe le point ![]() , i.e. une rotation de centre
, i.e. une rotation de centre ![]() , et on a
, et on a
![]() . Comme une homothétie de centre
. Comme une homothétie de centre ![]() commute avec toute transformation affine laissant
commute avec toute transformation affine laissant ![]() fixe, on a
fixe, on a
![]() .
.
Si
![]() est une décomposition de
est une décomposition de ![]() en produit (nécessairement commutatif) d'une homothétie de rapport
en produit (nécessairement commutatif) d'une homothétie de rapport ![]() et d'une rotation de même centre
et d'une rotation de même centre ![]() , on a
, on a ![]() et
et ![]() , puisque
, puisque ![]() est le seul point fixe de
est le seul point fixe de ![]() , d'où
, d'où ![]() et
et ![]() , ce qui établit l'unicité de la décomposition.
, ce qui établit l'unicité de la décomposition.![]()
Une similitude indirecte qui n'est pas une isométrie est donc caractérisée par son centre (l'unique point fixe), son rapport et son axe (l'axe de la réflexion de la décomposition précédente), qui est une droite passant par le centre.
Démonstration : Soit ![]() une similitude plane indirecte de rapport
une similitude plane indirecte de rapport ![]() différent de 1. D'après la proposition 63,
différent de 1. D'après la proposition 63, ![]() admet un point fixe
admet un point fixe ![]() et un seul. Soit
et un seul. Soit ![]() l'homothétie de centre
l'homothétie de centre ![]() et de rapport
et de rapport ![]() . La transformation affine
. La transformation affine
![]() est une isométrie indirecte laissant fixe le point
est une isométrie indirecte laissant fixe le point ![]() , i.e. une réflexion d'axe passant par
, i.e. une réflexion d'axe passant par ![]() , et on a
, et on a
![]() . Comme une homothétie de centre
. Comme une homothétie de centre ![]() commute avec toute transformation affine laissant
commute avec toute transformation affine laissant ![]() fixe, on a
fixe, on a
![]() .
.
Si
![]() est une décomposition de
est une décomposition de ![]() en produit (nécessairement commutatif) d'une homothétie de centre
en produit (nécessairement commutatif) d'une homothétie de centre ![]() et de rapport
et de rapport ![]() et d'une réflexion d'axe passant par
et d'une réflexion d'axe passant par ![]() , on a
, on a ![]() et
et ![]() , puisque
, puisque ![]() est le seul point fixe de
est le seul point fixe de ![]() , d'où
, d'où ![]() et
et ![]() , ce qui établit l'unicité de la décomposition.
, ce qui établit l'unicité de la décomposition.![]()
Similitudes planes et nombres complexes
Le corps
![]() des nombres complexes est un espace vectoriel de dimension 2 sur
des nombres complexes est un espace vectoriel de dimension 2 sur
![]() . Il est donc muni d'une structure naturelle de plan affine. La base canonique
. Il est donc muni d'une structure naturelle de plan affine. La base canonique ![]() de
de
![]() et l'origine 0 constituent un repère cartésien naturel pour ce plan. On appellera ce plan plan complexe. Réciproquement, le choix d'un repère cartésien
et l'origine 0 constituent un repère cartésien naturel pour ce plan. On appellera ce plan plan complexe. Réciproquement, le choix d'un repère cartésien
![]() permet d'identifier tout plan affine
permet d'identifier tout plan affine ![]() à
à
![]() , ou encore à
, ou encore à
![]() : au point
: au point ![]() de coordonnées
de coordonnées ![]() on associe le nombre complexe
on associe le nombre complexe ![]() , qu'on appelle affixe de
, qu'on appelle affixe de ![]() . On peut également définir l'affixe d'un vecteur : l'application qui au vecteur
. On peut également définir l'affixe d'un vecteur : l'application qui au vecteur
![]() de
de
![]() associe le nombre complexe
associe le nombre complexe ![]() est un isomorphisme d'espaces vectoriels, qui permet d'identifier
est un isomorphisme d'espaces vectoriels, qui permet d'identifier
![]() à
à
![]() . Cela permet de ramener certains problèmes géométriques à des problèmes d'algèbre.
. Cela permet de ramener certains problèmes géométriques à des problèmes d'algèbre.
Mais l'intérêt du plan complexe en géométrie vient surtout de ce qu'il possède aussi une structure euclidienne naturelle. En effet l'application
![]() est une norme euclidienne sur
est une norme euclidienne sur
![]() déduite du produit scalaire
déduite du produit scalaire
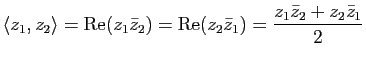
La distance de deux points ![]() et
et ![]() , d'affixes respectives
, d'affixes respectives ![]() et
et ![]() , est alors
, est alors
![]() . L'angle
. L'angle
![]() de deux vecteurs non nuls d'affixes respectives
de deux vecteurs non nuls d'affixes respectives ![]() et
et ![]() est
est
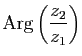 . En particulier, ces deux vecteurs sont colinéaires si et seulement si
. En particulier, ces deux vecteurs sont colinéaires si et seulement si
![]() est réel, et orthogonaux si et seulement si
est réel, et orthogonaux si et seulement si
![]() est imaginaire pur.
est imaginaire pur.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales