Section : Espaces affines euclidiens
Avant : Isométries, similitudes
Après : Entraînement

Géométrie du triangle et du cercle

Dans toute cette partie, triangle signifie triangle non aplati (sauf mention explicite du contraire). On note $ BC=a$, $ CA=b$, $ AB=c$ les longueurs des côtés d'un triangle $ ABC$ et $ \hat A$, $ \hat B$, $ \hat C$ les (mesures des) angles géométriques du triangle.

Un triangle $ ABC$ est dit rectangle en $ A$ si l'angle $ \hat A$ est droit ; le côté $ BC$ est alors appelé hypoténuse.

Il est dit acutangle si ses trois angles sont aigus, isocèle en $ A$ si les côtés $ AB$ et $ AC$ ont même longueur, équilatéral si ses trois côtés ont même longueur.

Proposition 68   Formule d'Al Kashi

Dans tout triangle $ ABC$, on a :

$\displaystyle a^2=b^2+c^2-2bc \cos \hat A \; .$

En particulier, un triangle $ ABC$ est rectangle en $ A$ si et seulement si $ a^2=b^2+c^2$ (théorème de Pythagore).

Démonstration : Par la relation de Chasles :

$\displaystyle a^2=\vv{BC}^2=(\vv{AC}-\vv{AB})^2=AC^2+AB^2-2 AC \times AB \times \cos \hat A =b^2+c^2-2bc \cos \hat A \; .$

$ \square$

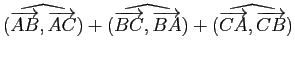Proposition 69   Pour tout triangle $ ABC$, la somme des angles orientés de vecteurs $ \widehat{(\vv{AB},\vv{AC})}+\widehat{(\vv{BC},\vv{BA})}+\widehat{(\vv{CA},\vv{CB})}$ est égale à l'angle plat. Les mesures principales de ces trois angles (comprises entre $ -\pi$ et $ +\pi$) ont même signe et la somme des mesures des angles géométriques du triangle est égale à $ \pi$.

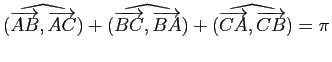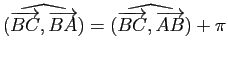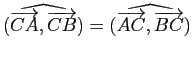Démonstration : L'égalité $ \widehat{(\vv{AB},\vv{AC})}+\widehat{(\vv{BC},\vv{BA})}+\widehat{(\vv{CA},\vv{CB})}=\pi$ (où on a identifié l'angle plat et sa mesure $ \pi$) découle de la relation de Chasles pour les angles orientés et des relations $ \widehat{(\vv{BC},\vv{BA})}=\widehat{(\vv{BC},\vv{AB})}+\pi$ et $ \widehat{(\vv{CA},\vv{CB})}=\widehat{(\vv{AC},\vv{BC})}$.

Les égalités $ \mathrm{det}(\vv{BC},\vv{BA})=\mathrm{det}(\vv{AC}-\vv{AB},-\vv{AB})=\mathrm{det}(\vv{AB},\vv{AC})$ et $ \mathrm{det}(\vv{CA},\vv{CB})=\mathrm{det}(\vv{AB},\vv{AC})$ montrent que les sinus de ces trois angles orientés ont le même signe. Il en résulte que la somme des mesures des angles géométriques $ \hat A$, $ \hat B$, $ \hat C$ du triangle est égale à $ \pi$.$ \square$

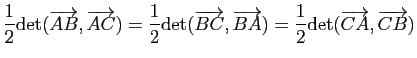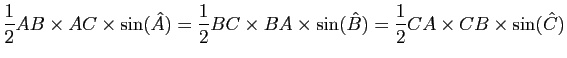Le réel $ \dfrac12 \mathrm{det}(\vv{AB},\vv{AC})=\dfrac12 \mathrm{det}(\vv{BC},\vv{BA})=\dfrac12 \mathrm{det}(\vv{CA},\vv{CB})$ est l'aire algébrique du triangle orienté $ ABC$. Sa valeur absolue est l'aire géométrique de ce triangle et s'écrit aussi $ \dfrac{1}{2}AB \times AC \times \sin(\hat A)= \dfrac{1}{2}BC \times BA \times \sin(\hat B)= \dfrac{1}{2}CA \times CB \times \sin(\hat C)$.

Elle est aussi égale au demi-produit de la longueur d'un des côtés par la longueur de la hauteur correspondante (distance de la droite portant ce côté au sommet opposé).

Médiatrices, cercle circonscrit

Proposition 70   Les trois médiatrices d'un triangle sont concourantes. Leur point de concours est l'unique point du plan équidistant des trois sommets. C'est aussi le centre de l'unique cercle du plan passant par ces trois sommets. Ce cercle est appelé cercle circonscrit au triangle.

Démonstration : Les médiatrices de deux côtés sont sécantes, sinon ces côtés seraient parallèles et le triangle aplati. Leur point d'intersection est équidistant des trois sommets du triangle et appartient donc à la troisième médiatrice.$ \square$

\includegraphics[width=0.6\textwidth]{mediatrices}

Hauteurs, orthocentre

Définition 33   On appelle hauteurs d'un triangle les droites perpendiculaires aux côtés passant par le sommet opposé.

Proposition 71   Les trois hauteurs d'un triangle sont concourantes en un point appelé orthocentre du triangle.

Démonstration : Les parallèles aux côtés menées par les sommets opposés déterminent un triangle $ A'B'C'$. Les hauteurs du triangle initial $ ABC$ sont les médiatrices du triangle $ A'B'C'$ : elles sont donc concourantes.$ \square$

\includegraphics[width=0.6\textwidth]{hauteurs1}

Bissectrices, cercles inscrit et exinscrits

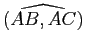Définition 34   On appelle bissectrice intérieure en $ A$ d'un triangle $ ABC$ la bissectrice du couple de demi-droites $ [AB)$ et $ [AC)$. L'autre bissectrice de l'angle de droites $ \widehat{(AB,AC)}$ est appelée bissectrice extérieure en $ A$ du triangle $ ABC$.

La proposition suivante justifie cette terminologie :

Proposition 72   La bissectrice intérieure en $ A$ d'un triangle $ ABC$ coupe le côté $ [BC]$ en un point $ A_1$ (appelé pied de cette bissectrice) qui est le barycentre du système pondéré $ [(B,b)$, $ (C,c)]$. La bissectrice extérieure en $ A$ est perpendiculaire à la bissectrice intérieure. Elle ne rencontre pas l'intérieur du triangle et coupe, si le triangle n'est pas isocèle en $ A$, la droite $ (BC)$ en un point $ A'_1$ qui est le barycentre du système pondéré $ [(B,b), \, (C,-c)]$. Les points $ A_1$ et $ A'_1$ sont donc les deux points de la droite $ (BC)$ vérifiant :

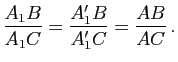
$\displaystyle \dfrac{A_1B}{A_1C}=\dfrac{A'_1B}{A'_1C}=\dfrac{AB}{AC} \, .$

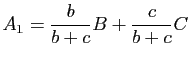Démonstration : Soit $ A_1=\dfrac{b}{b+c} B+\dfrac{c}{b+c} C$ le barycentre du système pondéré $ [(B,b)$, $ (C,c)]$. Le point $ A_1$ appartient au segment $ [BC]$ et les aires algébriques $ S_1$ et $ S_2$ des triangles $ ABA_1$ et $ AA_1C$ vérifient

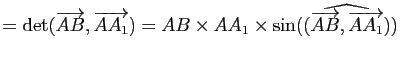$\displaystyle 2 S_1$ $\displaystyle = \mathrm{det}(\vv{AB},\vv{AA_1}) = AB \times AA_1 \times \sin(\widehat{(\vv{AB},\vv{AA_1})})$    
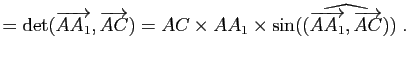$\displaystyle 2 S_2$ $\displaystyle = \mathrm{det}(\vv{AA_1},\vv{AC}) = AC \times AA_1 \times \sin(\widehat{(\vv{AA_1},\vv{AC})}) \; .$    

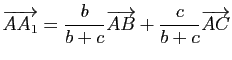Mais il ressort de l'égalité $ \vv{AA_1}=\dfrac{b}{b+c} \vv{AB} + \dfrac{c}{b+c} \vv{AC}$ que

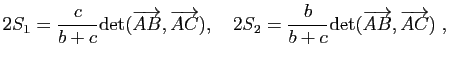
$\displaystyle 2 S_1= \dfrac{c}{b+c} \mathrm{det}(\vv{AB},\vv{AC}), \quad 2 S_2= \dfrac{b}{b+c} \mathrm{det}(\vv{AB},\vv{AC}) \; ,$

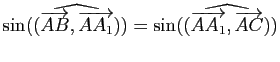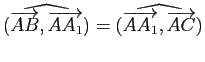d'où $ \sin(\widehat{(\vv{AB},\vv{AA_1})})= \sin(\widehat{(\vv{AA_1},\vv{AC})})$ et $ \widehat{(\vv{AB},\vv{AA_1})}= \widehat{(\vv{AA_1},\vv{AC})}$ (on ne peut avoir 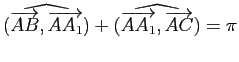$ \widehat{(\vv{AB},\vv{AA_1})} + \widehat{(\vv{AA_1},\vv{AC})}=\pi$ sinon le triangle serait aplati). Le point $ A_1$ appartient donc à la bissectrice intérieure en $ A$ du triangle $ ABC$.

La démonstration est analogue pour le point $ A'_1$.$ \square$

Proposition 73   Les bissectrices intérieures d'un triangle $ ABC$ sont concourantes en un point de coordonnées barycentriques $ (a,b,c)$ dans le repère affine $ (A,B,C)$. Ce point est centre d'un cercle tangent aux trois côtés du triangle, appelé cercle inscrit dans le triangle $ ABC$. Chaque bissectrice intérieure rencontre les bissectrices extérieures en les deux autres sommets en un point qui est également centre d'un cercle tangent aux trois côtés du triangle. Ces trois cercles sont appelés cercles exinscrits.

Il y a donc exactement quatre points équidistants des trois côtés d'un triangle ; chacun de ces points est intersection de trois bissectrices et centre d'un cercle tangent aux trois côtés.

Démonstration : Il suffit de vérifier que le point 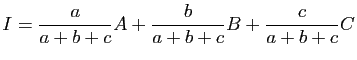$ I=\dfrac{a}{a+b+c} A + \dfrac{b}{a+b+c} B + \dfrac{c}{a+b+c} C$ appartient aux trois bissectrices intérieures du triangle. Ce point est intérieur au triangle. Les points de coordonnées barycentriques respectives $ (-a,b,c)$, $ (a,-b,c)$, $ (a,b,-c)$ sont extérieurs au triangle et appartiennent tous à deux bissectrices extérieures et une bissectrice intérieure. Ils sont ainsi équidistants des trois droites portant les côtés du triangle.$ \square$

\includegraphics[width=12cm]{exinscrits}

Cercles

Définition 35   Soit $ E$ un plan affine euclidien, $ O$ un point de $ E$ et $ R$ un réel positif. On appelle cercle de centre $ O$ et de rayon $ R$ l'ensemble des points $ M$ de $ E$ vérifiant $ OM=R$.

Si $ OM>R$ (resp. $ OM<R$), on dit que $ M$ est extérieur (resp. intérieur) au cercle.

Représentation paramétrique, équation

Dans le plan rapporté à un repère orthonormé $ (O,\vi,\vj)$, le cercle de centre $ \Omega (a,b)$ et de rayon $ R$ admet la représentation paramétrique :

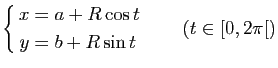$\displaystyle \left\{ \begin{aligned}x&=a+R\cos t\\ y&=b+R\sin t \end{aligned} \right. \qquad (t\in[0,2\pi[)$

Son équation cartésienne s'écrit $ (x-a)^2+(y-b)^2=R^2$, et est donc de la forme $ x^2+y^2-2ax-2by+c=0$, où $ c=a^2+b^2-R^2$. Réciproquement, une équation de cette forme est celle d'un cercle si $ a^2+b^2-c\geq 0$ (si $ a^2+b^2-c= 0$, ce cercle est réduit à un point ; si $ a^2+b^2-c< 0$, l'ensemble des points la vérifiant est vide).

Intersection d'une droite et d'un cercle, tangentes

Proposition 74   Soit, dans le plan affine euclidien, $ D$ une droite et $ C$ un cercle de centre $ O$ et de rayon $ R$. L'intersection de $ D$ et de $ C$ est :

Si $ d(O,D)=R$, l'unique point d'intersection de $ D$ et de $ C$ est le projeté orthogonal $ H$ de $ O$ sur $ D$. On dit alors que $ D$ est tangente à $ C$ en $ H$. La tangente à un cercle de centre $ O$ en un point $ M$ de ce cercle est donc la perpendiculaire menée par $ M$ au rayon $ OM$.


Cette définition de la tangente, particulière au cercle, coïncide avec la définition usuelle de la tangente à une courbe paramétrée comme position limite d'une sécante, comme on le vérifie immédiatement en partant de la représentation paramétrique.

Positions relatives de deux cercles

Proposition 75   Soient $ C$ et $ C'$ deux cercles distincts du plan affine euclidien, de centres respectifs $ O$ et $ O'$ et de rayons $ R$ et $ R'$. On note $ d=OO'$ la distance de leurs centres. Alors cinq cas sont possibles :

Puissance d'un point par rapport à un cercle

Proposition 76   Soit $ C$ un cercle de centre $ O$ et de rayon $ R$, $ M$ un point du plan et $ D$ une droite passant par $ M$ et coupant $ C$ en deux points $ A$ et $ B$. Alors le produit scalaire $ \vv{MA}\cdot\vv{MB}$ est égal à $ MO^2-R^2$ et ne dépend donc pas de la droite $ D$. Ce nombre est appelé puissance de $ M$ par rapport au cercle $ C$ et noté $ p_C(M)$.

\includegraphics[height=5cm]{puissance}
Démonstration : Soit $ A'$ le point diamétralement opposé à $ A$ sur le cercle $ C$. On a :

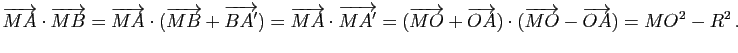
$\displaystyle \vv{MA}\cdot \vv{MB}=\vv{MA}\cdot (\vv{MB}+\vv{BA'}) =\vv{MA}\cdot \vv{MA'} =(\vv{MO}+\vv{OA})\cdot (\vv{MO}-\vv{OA}) =MO^2-R^2 \, .$

$ \square$

Ce nombre permet de situer le point $ M$ par rapport au cercle. Plus précisément :

En particulier, si le point $ M$ est extérieur au cercle, on a $ p_C(M)=MT^2=MT'^2$, où $ T$ et $ T'$ sont les points de contact des deux tangentes menées par $ M$ au cercle $ C$.

Expression analytique. Le plan étant rapporté à un repère orthonormé, la puissance du point $ M(x,y)$ par rapport au cercle $ C$ d'équation $ x^2+y^2-2ax-2by+c=0$ est $ p_C(M)=x^2+y^2-2ax-2by+c$.

Axe radical de deux cercles

Proposition 77   Soient $ C$ et $ C'$ deux cercles distincts du plan affine euclidien. L'ensemble des points du plan ayant même puissance par rapport à $ C$ et $ C'$ est :

Cette droite est alors appelée axe radical des deux cercles.

Dans le cas où les cercles sont sécants, leur axe radical est la droite passant par les deux points d'intersection de ces cercles. Dans le cas où ils sont tangents, leur axe radical est leur tangente commune.

Faisceaux linéaires de cercles

Définition 36   Soient $ C_1$ et $ C_2$ deux cercles non concentriques du plan affine euclidien. On appelle faisceau de cercles engendré par $ C_1$ et $ C_2$ l'ensemble des cercles $ C$ du plan tels que l'axe radical de $ C$ et $ C_1$ soit égal à l'axe radical de $ C_1$ et $ C_2$.

Proposition 78   Soient $ C_1$ et $ C_2$ deux cercles non concentriques du plan affine euclidien rapporté à un repère orthonormé, d'équations respectives $ f_1(x,y)=0$ et $ f_2(x,y)=0$. Le faisceau de cercles engendré par $ C_1$ et $ C_2$ est l'ensemble des cercles du plan d'équation $ \alpha f_1(x,y)+(1-\alpha)f_2(x,y)=0$, pour $ \alpha\in \mathbb{R}$.

On a supposé ici les équations normalisées (les coefficients de $ x^2$ et $ y^2$ égaux à 1). L'équation $ f_1(x,y)-f_2(x,y)=0$ est alors l'équation de l'axe radical de deux quelconques des cercles du faisceau.

Théorème de l'angle inscrit, cocyclicité

Proposition 79 (Théorème de l'angle inscrit)   .

Soient $ A$, $ B$ et $ C$ trois points distincts d'un cercle de centre $ O$, $ T_B$ la tangente en $ B$ à ce cercle. Alors on a les égalités d'angles orientés de vecteurs :

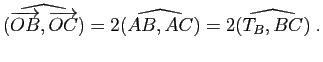
$\displaystyle \widehat{(\vv{OB},\vv{OC})}=2 \widehat{(AB,AC)}=2\widehat{(T_B,BC)} \; .$


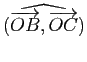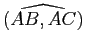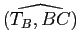L'angle $ \widehat{(\vv{OB},\vv{OC})}$ est un angle orienté de vecteurs, et les angles $ \widehat{(AB,AC)}$ et $ \widehat{(T_B,BC)}$ des angles orientés de droites ; mais 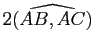$ 2\widehat{(AB,AC)}$ (resp. 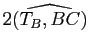$ 2\widehat{(T_B,BC)}$) est alors aussi un angle orienté de vecteurs (dont la mesure, en supposant le plan orienté, est définie modulo $ 2\pi$).

Démonstration : Soit $ s_1$ (resp. $ s_2$) la réflexion d'axe la médiatrice $ \Delta_1$ de $ [AB]$ (resp. la médiatrice $ \Delta_2$ de $ [AC]$). La composée $ s_2 \circ s_1$ est une rotation de centre $ O$ (puisque $ \Delta_1$ et $ \Delta_2$ se coupent en $ O$) qui transforme $ B$ en $ C$. Son angle est donc 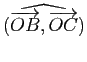$ \widehat{(\vv{OB},\vv{OC})}$ ; mais c'est aussi 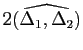$ 2\widehat{(\Delta_1,\Delta_2)}$ d'après la proposition 24, qui est égal à 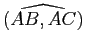$ \widehat{(AB,AC)}$, puisque $ \Delta_1$ est orthogonale à $ (AB)$ et $ \Delta_2$ à $ (AC)$.

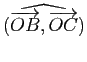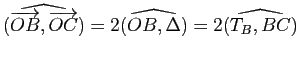De même, si $ s_4$ est la réflexion d'axe la médiatrice $ \Delta$ de $ [BC]$ et $ s_3$ la réflexion d'axe $ (OB)$, la composée $ s_4\circ s_3$ est la rotation de centre $ O$ transformant $ B$ en $ C$, i.e. la rotation de centre $ O$ et d'angle $ \widehat{(\vv{OB},\vv{OC})}$, d'où $ \widehat{(\vv{OB},\vv{OC})}=2\widehat{(OB,\Delta)}=2\widehat{(T_B,BC)}$, puisque les droites $ (OB)$ et $ \Delta$ sont respectivement orthogonales à $ (OB)$ et $ (BC)$.$ \square$

\includegraphics[width=0.45\textwidth]{inscrit} \includegraphics[width=0.45\textwidth]{inscrit2}

Remarque : l'égalité impliquant la tangente peut être vue comme le cas limite de l'égalité précédente quand le point $ A$ tend vers le point $ B$.

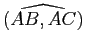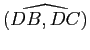Proposition 80   Quatre points distincts $ A$, $ B$, $ C$, $ D$ du plan sont cocycliques ou alignés si et seulement si les angles orientés de droites $ \widehat{(AB,AC)}$ et $ \widehat{(DB,DC)}$ sont égaux.

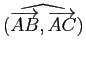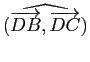Plus précisément, ils sont alignés si et seulement si ces deux angles de droites sont nuls (ce qui revient à dire que les angles de vecteurs $ \widehat{(\vv{AB},\vv{AC})}$ et $ \widehat{(\vv{DB},\vv{DC})}$ sont nuls ou plats), cocycliques si ces angles sont égaux mais non nuls.

Démonstration : Le cas des points alignés est trivial.

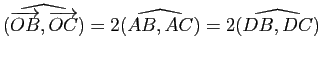Si les quatre points sont cocycliques et si $ O$ est le centre du cercle les contenant, le théorème de l'angle inscrit nous dit que $ \widehat{(\vv{OB},\vv{OC})}=2 \widehat{(AB,AC)}=2\widehat{(DB,DC)}$ (égalité d'angles orientés de vecteurs). Il en résulte que 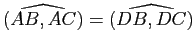$ \widehat{(AB,AC)}=\widehat{(DB,DC)}$ (égalité d'angles orientés de droites).

Réciproquement, si 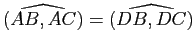$ \widehat{(AB,AC)}=\widehat{(DB,DC)}$ n'est pas l'angle nul, les triangles $ ABC$ et $ DBC$ ne sont pas aplatis. Soient alors $ \Gamma_1$ et $ \Gamma_2$ les cercles circonscrits à ces triangles, $ T_1$ et $ T_2$ les tangentes en $ B$ à ces cercles. Il résulte de la proposition 79 que $ T_1=T_2$. Les deux cercles $ \Gamma_1$ et $ \Gamma_2$ ont même tangente en $ B$ et passent par les deux points $ B$ et $ C$ : ils sont donc confondus et les points $ A$, $ B$, $ C$ et $ D$ sont cocycliques.$ \square$


Section : Espaces affines euclidiens
Avant : Isométries, similitudes
Après : Entraînement


         © UJF Grenoble, 2011                              Mentions légales