Proposition 14
Soit  une application linéaire d'un espace vectoriel euclidien
une application linéaire d'un espace vectoriel euclidien  dans lui-même. Les propriétés suivantes sont équivalentes :
dans lui-même. Les propriétés suivantes sont équivalentes :
 conserve le produit scalaire :
conserve le produit scalaire :
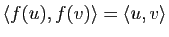 pour tout couple
pour tout couple
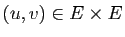 ;
;
 conserve la norme :
conserve la norme :
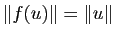 pour tout
pour tout 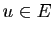 ;
;
- l'image par
 de toute base orthonormée de
de toute base orthonormée de  est une base orthonormée ;
est une base orthonormée ;
- il existe une base orthonormée de
 dont l'image par
dont l'image par  est une base orthonormée ;
est une base orthonormée ;
- il existe une base orthonormée de
 dans laquelle la matrice de
dans laquelle la matrice de  est orthogonale ;
est orthogonale ;
- la matrice de
 dans toute base orthonormée de
dans toute base orthonormée de  est orthogonale.
est orthogonale.
Définition 11
Une application linéaire de  dans
dans  vérifiant ces propriétés équivalentes est appelée transformation orthogonale ou automorphisme orthogonal de
vérifiant ces propriétés équivalentes est appelée transformation orthogonale ou automorphisme orthogonal de  .
.
Démonstration : L'équivalence de 4 et 5, de même que celle de 6 et 3, provient de la proposition 9, l'implication
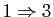 de la définition d'une transformation orthogonale, l'implication
de la définition d'une transformation orthogonale, l'implication
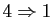 de l'expression du produit scalaire dans une base orthonormale, les implications
de l'expression du produit scalaire dans une base orthonormale, les implications
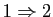 et
et
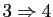 sont triviales. Il reste à montrer l'implication
sont triviales. Il reste à montrer l'implication
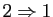 . Si
. Si  est linéaire et conserve les normes, alors
est linéaire et conserve les normes, alors
pour tout couple 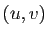 .
.
Il résulte de la proposition suivante que toute application d'un espace vectoriel euclidien dans lui-même qui conserve le produit scalaire est une transformation orthogonale (mais une application qui conserve seulement la norme n'est pas nécessairement linéaire) :
Proposition 15
Soit  un espace vectoriel euclidien et
un espace vectoriel euclidien et  une application de
une application de  dans
dans  qui conserve le produit scalaire :
qui conserve le produit scalaire :
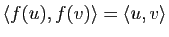 pour tout couple
pour tout couple 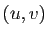 de vecteurs de
de vecteurs de  . Alors
. Alors  est linéaire.
est linéaire.
Démonstration : La conservation du produit scalaire entraîne :
d'où
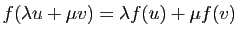 pour tout couple
pour tout couple
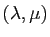 de réels et tout couple
de réels et tout couple 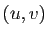 de vecteurs de
de vecteurs de  .
.
Exemple : les symétries orthogonales
Proposition 16
Une symétrie vectorielle est une transformation orthogonale si et seulement si c'est une symétrie orthogonale.
Démonstration : Soit  la symétrie par rapport à un sous-espace vectoriel
la symétrie par rapport à un sous-espace vectoriel 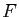 dans la direction du sous-espace vectoriel
dans la direction du sous-espace vectoriel  . Si
. Si 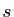 est une transformation orthogonale, elle conserve le produit scalaire, d'où, pour tout vecteur
est une transformation orthogonale, elle conserve le produit scalaire, d'où, pour tout vecteur  de
de 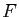 et tout vecteur
et tout vecteur  de
de 
d'où
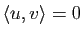 , ce qui montre que
, ce qui montre que 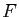 et
et  sont orthogonaux.
sont orthogonaux.
Réciproquement, si 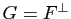 , tout vecteur
, tout vecteur 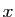 s'écrit
s'écrit 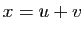 , avec
, avec 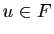 et
et 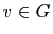 , et
, et 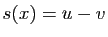 , d'où
, d'où
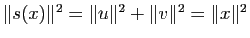 , puisque
, puisque
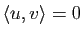 , ce qui montre que
, ce qui montre que 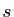 est une transformation orthogonale.
est une transformation orthogonale.
Groupe orthogonal
Rappel : Soit
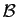 une base orthonormée d'un espace vectoriel euclidien
une base orthonormée d'un espace vectoriel euclidien  de dimension
de dimension 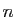 . L'application qui à toute application linéaire bijective de
. L'application qui à toute application linéaire bijective de  dans
dans  associe sa matrice dans la base
associe sa matrice dans la base
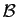 est un isomorphisme du groupe
est un isomorphisme du groupe 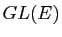 sur le groupe
sur le groupe
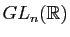 des matrices réelles carrées d'ordre
des matrices réelles carrées d'ordre 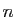 . La restriction de cet isomorphisme à
. La restriction de cet isomorphisme à  est un isomorphisme de
est un isomorphisme de  sur le groupe
sur le groupe 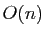 des matrices orthogonales d'ordre
des matrices orthogonales d'ordre 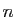 .
.
Le groupe orthogonal en dimension 2
Dans cette partie,  est un plan vectoriel euclidien orienté.
est un plan vectoriel euclidien orienté.
Proposition 18
Toute matrice orthogonale  d'ordre 2 est de l'une des deux formes suivantes :
d'ordre 2 est de l'une des deux formes suivantes :
-
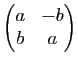 où
où 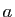 et
et 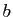 sont deux réels vérifiant
sont deux réels vérifiant 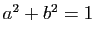 si
si
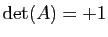 ;
;
-
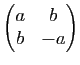 où
où 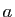 et
et 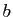 sont deux réels vérifiant
sont deux réels vérifiant 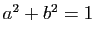 si
si
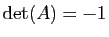 .
.
Proposition 19
L'application qui à un réel 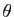 associe la matrice
associe la matrice
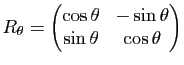 est un homomorphisme surjectif du groupe additif
est un homomorphisme surjectif du groupe additif
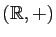 sur le groupe multiplicatif
sur le groupe multiplicatif 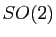 .
Son noyau est le sous-groupe
.
Son noyau est le sous-groupe
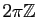 des multiples entiers de
des multiples entiers de 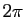 .
Il en résulte que
.
Il en résulte que 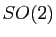 est isomorphe au groupe additif
est isomorphe au groupe additif
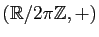 des réels modulo
des réels modulo 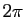 .
.
Démonstration : La proposition découle immédiatement des formules d'addition des fonctions trigonométriques :

Un élément de 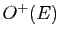 est appelé rotation vectorielle.
est appelé rotation vectorielle.
Corollaire 2
Le groupe 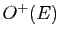 des rotations vectorielles planes est commutatif, isomorphe au groupe additif
des rotations vectorielles planes est commutatif, isomorphe au groupe additif
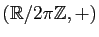 des réels modulo
des réels modulo 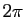 .
.
Corollaire 3
La matrice d'une rotation vectorielle est la même dans toute base orthonormée directe.
Démonstration : Cela découle immédiatement de la commutativité de 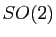 ; en effet si une rotation vectorielle a pour matrice
; en effet si une rotation vectorielle a pour matrice
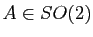 dans une base orthonormée directe, sa matrice dans une autre base orthonormée directe sera de la forme
dans une base orthonormée directe, sa matrice dans une autre base orthonormée directe sera de la forme 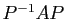 , où la matrice de passage
, où la matrice de passage 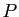 appartient aussi à
appartient aussi à 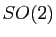 ; comme
; comme 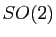 est abélien, on a
est abélien, on a
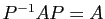 .
.
Il en résulte que l'isomorphisme du corollaire 2 ne dépend pas du choix d'une base orthonormée directe.
Remarque :
La rotation de matrice 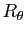 dans une base orthonormée directe a pour matrice
dans une base orthonormée directe a pour matrice
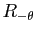 dans une base orthonormée indirecte. Changer l'orientation du plan revient donc à changer le signe de
dans une base orthonormée indirecte. Changer l'orientation du plan revient donc à changer le signe de 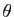 .
.
Proposition 20
Tout élément de 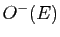 est une réflexion vectorielle (symétrie orthogonale par rapport à une droite vectorielle).
est une réflexion vectorielle (symétrie orthogonale par rapport à une droite vectorielle).
Démonstration : Le polynôme caractéristique d'une matrice
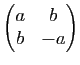 avec
avec 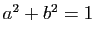 est
est 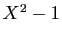 , cette matrice est donc semblable à la matrice
, cette matrice est donc semblable à la matrice
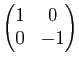 , ce qui montre que toute transformation orthogonale négative du plan est une symétrie par rapport à une droite. Cette symétrie est une symétrie orthogonale d'après la proposition 16 .
, ce qui montre que toute transformation orthogonale négative du plan est une symétrie par rapport à une droite. Cette symétrie est une symétrie orthogonale d'après la proposition 16 .
Proposition 21
Pour tout couple 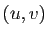 de vecteurs unitaires de
de vecteurs unitaires de  , il existe une rotation vectorielle
, il existe une rotation vectorielle 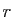 et une seule transformant le premier en le second, i.e. telle que
et une seule transformant le premier en le second, i.e. telle que 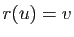 .
.
Démonstration : On complète  en une base orthonormée directe
en une base orthonormée directe 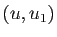 de
de  . Dans cette base,
. Dans cette base,  s'écrit
s'écrit 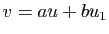 ,
où
,
où 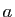 et
et 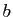 sont deux réels vérifiant
sont deux réels vérifiant 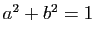 . Une rotation vectorielle
. Une rotation vectorielle 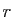 vérifie
vérifie 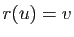 si et seulement si la première colonne de sa matrice dans cette base a pour coefficients
si et seulement si la première colonne de sa matrice dans cette base a pour coefficients 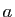 et
et 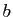 ; or il existe une et une seule matrice de
; or il existe une et une seule matrice de 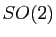 ayant cette propriété.
ayant cette propriété.
Angles
On se propose dans cette partie de définir les principales notions d'angles utilisées en géométrie plane. La notion première sera celle d'angle orienté de vecteurs ou, ce qui revient au même, d'angle orienté de demi-droites vectorielles. En effet l'angle de deux vecteurs non nuls  et
et  sera, par définition, l'angle des deux vecteurs unitaires
sera, par définition, l'angle des deux vecteurs unitaires
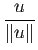 et
et
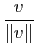 qui leur sont directement proportionnels ; or toute demi-droite vectorielle possède un vecteur directeur unitaire et un seul, et tout vecteur non nul définit une demi-droite vectorielle de manière unique. L'angle de deux vecteurs non nuls
qui leur sont directement proportionnels ; or toute demi-droite vectorielle possède un vecteur directeur unitaire et un seul, et tout vecteur non nul définit une demi-droite vectorielle de manière unique. L'angle de deux vecteurs non nuls  et
et  , ou l'angle des deux demi-droites vectorielles
, ou l'angle des deux demi-droites vectorielles
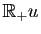 et
et
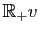 qu'ils engendrent, sera donc simplement l'angle des vecteurs unitaires
qu'ils engendrent, sera donc simplement l'angle des vecteurs unitaires
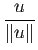 et
et
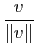 . Dans toute la suite, nous ne considérerons donc essentiellement que des vecteurs unitaires.
. Dans toute la suite, nous ne considérerons donc essentiellement que des vecteurs unitaires.
Deux approches sont proposées : la première, rapide et concrète, consiste à identifier un angle et sa mesure, c'est-à-dire à considérer un angle orienté de vecteurs comme une classe d'équivalence de réels modulo 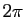 ; la seconde, plus abstraite, définit un angle comme une classe d'équivalence de couples de vecteurs et permet de distinguer l'angle de sa mesure (qui dépend de l'orientation du plan, alors que l'angle lui-même n'en dépend pas). Les deux approches reposent sur la même idée : l'angle de deux vecteurs est l'angle de l'unique rotation qui transforme le premier en le second (l'existence et l'unicité de cette rotation sont assurées par la proposition 21).
; la seconde, plus abstraite, définit un angle comme une classe d'équivalence de couples de vecteurs et permet de distinguer l'angle de sa mesure (qui dépend de l'orientation du plan, alors que l'angle lui-même n'en dépend pas). Les deux approches reposent sur la même idée : l'angle de deux vecteurs est l'angle de l'unique rotation qui transforme le premier en le second (l'existence et l'unicité de cette rotation sont assurées par la proposition 21).
Une remarque sur la terminologie : dans l'expression «angle orienté de vecteurs», «orienté» ne se réfère pas à l'orientation du plan, mais à l'ordre dans lequel sont écrits les vecteurs (l'angle
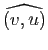 est l'opposé de l'angle
est l'opposé de l'angle
 ). On verra par contre que cet ordre est indifférent quand on parle d'angles géométriques.
). On verra par contre que cet ordre est indifférent quand on parle d'angles géométriques.
Angles : première approche
Angles orientés de vecteurs
Soient  et
et  deux vecteurs unitaires du plan vectoriel euclidien orienté
deux vecteurs unitaires du plan vectoriel euclidien orienté  . Il existe une et une seule rotation vectorielle
. Il existe une et une seule rotation vectorielle 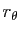 transformant
transformant  en
en  . La matrice de cette rotation est la même dans toute base orthonormée directe et s'écrit
. La matrice de cette rotation est la même dans toute base orthonormée directe et s'écrit
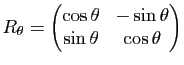 ,
où le réel
,
où le réel 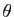 est uniquement déterminé modulo
est uniquement déterminé modulo 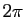 . On définit alors l'angle orienté
. On définit alors l'angle orienté
 des deux vecteurs comme la classe
des deux vecteurs comme la classe
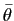 de
de 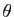 dans
dans
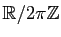 . On dira, pour abréger, qu'un angle orienté de deux vecteurs est un réel défini modulo
. On dira, pour abréger, qu'un angle orienté de deux vecteurs est un réel défini modulo 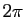 , et on appellera mesure principale de cet angle l'unique représentant de cette classe dans
, et on appellera mesure principale de cet angle l'unique représentant de cette classe dans
![$ ]-\pi,+\pi]$](img257.gif) .
Au niveau des notations, on ne distinguera plus un réel
.
Au niveau des notations, on ne distinguera plus un réel 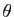 de sa classe
de sa classe
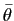 modulo
modulo 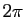 .
.
Remarque : la matrice de cette même rotation dans toute base orthonormée indirecte est
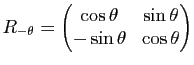 . Changer l'orientation du plan change donc les angles en leurs opposés.
. Changer l'orientation du plan change donc les angles en leurs opposés.
Angles particuliers :
Pour tout vecteur  , l'angle
, l'angle
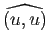 est l'angle nul et l'angle
est l'angle nul et l'angle
 est l'angle plat, de mesure principale
est l'angle plat, de mesure principale 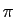 . Si
. Si  et
et  sont deux vecteurs orthogonaux, l'angle
sont deux vecteurs orthogonaux, l'angle
 est un angle droit, de mesure principale
est un angle droit, de mesure principale 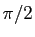 ou
ou 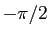 .
.
Proposition 22
Relation de Chasles pour les angles
Pour tout triplet 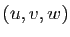 de vecteurs non nuls, on a :
de vecteurs non nuls, on a :
En particulier, les angles
 et
et
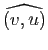 sont opposés.
sont opposés.
Démonstration : Si
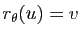 et
et
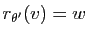 , alors
, alors
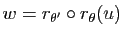 .
La relation de Chasles découle alors immédiatement de l'égalité
.
La relation de Chasles découle alors immédiatement de l'égalité
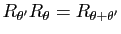 ,
,
Démonstration :
La première propriété résulte immédiatement de la commutativité du groupe 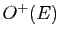 : en effet, l'unique rotation
: en effet, l'unique rotation 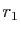 qui transforme
qui transforme  en
en  transforme aussi
transforme aussi 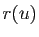 en
en 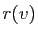 , puisque
, puisque
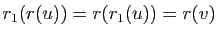 .
.
Pour démontrer la seconde, il suffit de remarquer que si 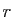 est une rotation et
est une rotation et 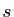 une réflexion, alors
une réflexion, alors 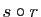 est une réflexion, d'où
est une réflexion, d'où
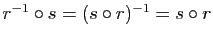 . Il en résulte que si
. Il en résulte que si 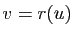 , alors
, alors
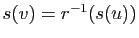 .
.
Angles orientés de droites
Une droite vectorielle a deux vecteurs directeurs unitaires et ces vecteurs sont opposés. Pour définir l'angle orienté de deux droites vectorielles, on a donc a priori le choix entre quatre angles de vecteurs :
 ,
,
 ,
,
 et
et
 (en fait deux, puisque
(en fait deux, puisque
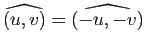 et
et
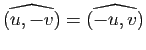 ). Il faut identifier ces deux angles, qui diffèrent d'un angle plat : l'angle orienté de deux droites est donc un réel défini modulo
). Il faut identifier ces deux angles, qui diffèrent d'un angle plat : l'angle orienté de deux droites est donc un réel défini modulo 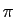 , i.e. un élément de
, i.e. un élément de
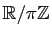 . La relation de Chasles est encore vraie pour les angles orientés de droites, qui sont également conservés par toute rotation et transformés en leurs opposés par les réflexions.
. La relation de Chasles est encore vraie pour les angles orientés de droites, qui sont également conservés par toute rotation et transformés en leurs opposés par les réflexions.
Angles géométriques
L'angle géométrique de deux vecteurs  et
et  est simplement la valeur absolue de la mesure principale de
est simplement la valeur absolue de la mesure principale de
 . C'est donc un réel compris entre 0 et
. C'est donc un réel compris entre 0 et 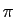 , et ce réel ne dépend pas de l'ordre des deux vecteurs. De plus toute tranformation orthogonale (directe ou indirecte) conserve les angles géométriques. Par contre, la relation de Chasles n'est plus toujours vraie pour les angles géométriques.
, et ce réel ne dépend pas de l'ordre des deux vecteurs. De plus toute tranformation orthogonale (directe ou indirecte) conserve les angles géométriques. Par contre, la relation de Chasles n'est plus toujours vraie pour les angles géométriques.
En particulier, l'angle géométrique de deux vecteurs unitaires  et
et  est égal à
est égal à
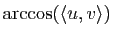 .
.
Bissectrices
Pour tout couple de vecteurs unitaires  et
et  , il existe une et une seule réflexion vectorielle
, il existe une et une seule réflexion vectorielle 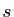 qui échange
qui échange  et
et  . Son axe est une droite vectorielle appelée bissectrice du couple
. Son axe est une droite vectorielle appelée bissectrice du couple 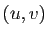 (ou du couple de demi-droites vectorielles engendrées respectivement par
(ou du couple de demi-droites vectorielles engendrées respectivement par  et
et  ), dirigée par le vecteur
), dirigée par le vecteur 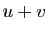 si
si  et
et  ne sont pas opposés. Un vecteur directeur unitaire
ne sont pas opposés. Un vecteur directeur unitaire 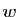 de cet axe vérifie
de cet axe vérifie
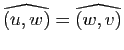 , ou encore
, ou encore
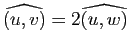 et cette relation détermine
et cette relation détermine  uniquement modulo
uniquement modulo  .
.
Pour tout couple 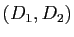 de droites vectorielles, il existe exactement deux réflexions vectorielles les échangeant. Les axes de ces réflexions sont des droites vectorielles orthogonales, qui sont appelées bissectrices du couple de droites.
de droites vectorielles, il existe exactement deux réflexions vectorielles les échangeant. Les axes de ces réflexions sont des droites vectorielles orthogonales, qui sont appelées bissectrices du couple de droites.
Composée de deux réflexions vectorielles
Proposition 24
Soient 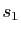 et
et 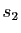 deux réflexions vectorielles, d'axes respectifs
deux réflexions vectorielles, d'axes respectifs 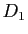 et
et 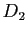 . Le composé
. Le composé
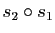 de ces deux réflexions est la rotation vectorielle d'angle
de ces deux réflexions est la rotation vectorielle d'angle
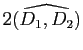 (l'angle de droites
(l'angle de droites
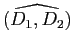 est seulement déterminé modulo
est seulement déterminé modulo 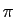 , mais
, mais
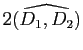 est bien défini modulo
est bien défini modulo 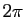 : c'est un angle orienté de vecteurs).
: c'est un angle orienté de vecteurs).
Démonstration : Soient 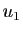 et
et 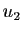 des vecteurs directeurs unitaires de
des vecteurs directeurs unitaires de 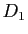 et
et 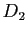 . Le composé
. Le composé
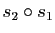 des deux réflexions
des deux réflexions 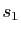 et
et 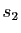 est une rotation vectorielle d'angle
est une rotation vectorielle d'angle
Mais d'après la proposition 23, on a :
L'angle de
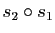 est donc
est donc
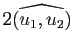 .
.
Angles : seconde approche
Angles orientés de vecteurs
Soit 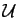 l'ensemble des vecteurs unitaires de
l'ensemble des vecteurs unitaires de  .
L'idée est la même que précédemment : on voudrait que l'angle
.
L'idée est la même que précédemment : on voudrait que l'angle
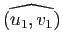 soit égal à l'angle
soit égal à l'angle
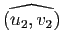 si c'est la même rotation qui transforme, pour chacun de ces couples, le premier vecteur en le second. La procédure standard pour cela est de définir une relation d'équivalence sur l'ensemble
si c'est la même rotation qui transforme, pour chacun de ces couples, le premier vecteur en le second. La procédure standard pour cela est de définir une relation d'équivalence sur l'ensemble
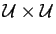 des couples de vecteurs unitaires de
des couples de vecteurs unitaires de  :
:
Proposition 25
La relation
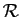 définie sur l'ensemble
définie sur l'ensemble
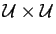 des couples de vecteurs unitaires de
des couples de vecteurs unitaires de  par :
est une relation d'équivalence.
par :
est une relation d'équivalence.
On a vu (proposition 21) qu'il existe toujours une rotation 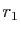 et une seule vérifiant
et une seule vérifiant
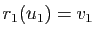 et une rotation
et une rotation 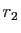 et une seule vérifiant
et une seule vérifiant
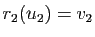 ; la relation
; la relation 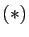 signifie que les couples
signifie que les couples 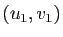 et
et 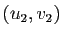 sont en relation si et seulement si
sont en relation si et seulement si 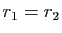 .
.
Remarques :
1) Cette relation est tout à fait analogue à celle qui définit l'équipollence de bipoints : si on veut définir les vecteurs à partir des points, on dit que deux couples 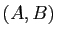 et
et 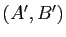 de points sont équipollents si c'est la même translation qui transforme
de points sont équipollents si c'est la même translation qui transforme  en
en 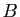 et
et 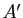 en
en 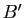 .
.
2) On montre facilement, en utilisant la commutativité de 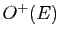 , que la relation
, que la relation  équivaut encore à :
équivaut encore à :
Définition 12
On appelle angle de deux vecteurs unitaires  et
et  , et on note
, et on note
 la classe d'équivalence du couple
la classe d'équivalence du couple 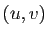 pour la relation
pour la relation
 .
.
On a donc bien
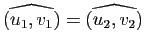 si et seulement si
si et seulement si 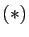 (ou
(ou 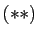 ) est vérifiée.
) est vérifiée.
On a défini les angles. On voudrait maintenant définir une addition sur l'ensemble  des angles. Il suffit pour cela de transporter sur
des angles. Il suffit pour cela de transporter sur  la loi de composition naturelle sur
la loi de composition naturelle sur 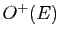 . L'ensemble
. L'ensemble  est en effet en bijection naturelle avec
est en effet en bijection naturelle avec 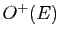 :
:
Proposition 26
L'application qui à une rotation
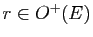 associe l'angle
associe l'angle
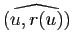 ne dépend pas du choix du vecteur unitaire
ne dépend pas du choix du vecteur unitaire 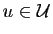 . C'est une bijection de
. C'est une bijection de 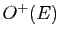 sur
sur  , et la bijection réciproque associe à un angle
, et la bijection réciproque associe à un angle
 l'unique rotation
l'unique rotation 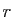 vérifiant
vérifiant 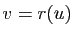 (cette rotation ne dépend pas du représentant choisi pour l'angle).
(cette rotation ne dépend pas du représentant choisi pour l'angle).
Définition 13
La somme
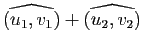 de deux angles est l'angle
de deux angles est l'angle
 , où
, où 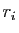 (
(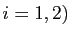 est l'unique rotation de
est l'unique rotation de  vérifiant
vérifiant
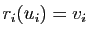 .
.
On vérifie immédiatement que  muni de cette addition est un groupe abélien isomorphe à
muni de cette addition est un groupe abélien isomorphe à 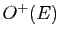 (on a tout fait pour cela). On récupère de plus immédiatement la relation de Chasles :
(on a tout fait pour cela). On récupère de plus immédiatement la relation de Chasles :
Proposition 27
Pour tout triplet 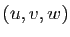 de vecteurs unitaires de
de vecteurs unitaires de  , on a :
, on a :
Démonstration : Il suffit de remarquer que si 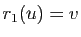 et
et 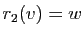 , alors
, alors
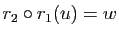 .
.
Angles particuliers
L'angle nul est bien sûr l'élément neutre du groupe 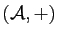 des angles de vecteurs ; c'est l'angle
des angles de vecteurs ; c'est l'angle
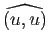 pour tout vecteur unitaire
pour tout vecteur unitaire  ; il correspond, dans l'isomorphisme précédent, à la rotation identité
; il correspond, dans l'isomorphisme précédent, à la rotation identité 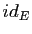 . Un autre angle remarquable est l'angle plat
. Un autre angle remarquable est l'angle plat 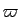 qui est l'angle
qui est l'angle
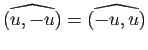 pour tout vecteur unitaire
pour tout vecteur unitaire  ; il correspond à la rotation vectorielle
; il correspond à la rotation vectorielle 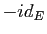 ; c'est l'unique élément d'ordre 2 du groupe
; c'est l'unique élément d'ordre 2 du groupe 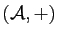 :
:
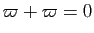 . Le groupe
. Le groupe  possède en outre deux éléments d'ordre 4, qui sont les angles droits : ce sont les angles
possède en outre deux éléments d'ordre 4, qui sont les angles droits : ce sont les angles
 et
et
 où
où 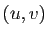 est une base orthonormée quelconque de
est une base orthonormée quelconque de  .
.
Angles géométriques
Un angle géométrique doit être invariant par toute transformation orthogonale (et non plus simplement par les seules rotations). On identifie donc cette fois deux couples de vecteurs unitaires s'il existe une transformation orthogonale  qui transforme le premier en le second :
qui transforme le premier en le second : 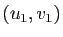 et
et 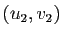 sont équivalents si et seulement si il existe
sont équivalents si et seulement si il existe
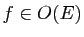 vérifiant
vérifiant
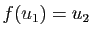 et
et
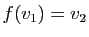 .
Cela revient à quotienter
.
Cela revient à quotienter  par la relation d'équivalence pour laquelle deux angles sont équivalents s'ils sont égaux ou opposés.
par la relation d'équivalence pour laquelle deux angles sont équivalents s'ils sont égaux ou opposés.
Angles orientés de droites
La manière naturelle de définir l'angle de deux droites vectorielles 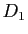 et
et 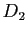 est de prendre un vecteur directeur unitaire
est de prendre un vecteur directeur unitaire 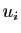 sur chacune de ces droites et de définir
sur chacune de ces droites et de définir
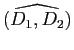 comme étant
comme étant
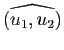 . Comme une droite vectorielle possède deux vecteurs directeurs unitaires opposés, on obtient ainsi a priori quatre valeurs, qui se réduisent en fait à deux, puisque
. Comme une droite vectorielle possède deux vecteurs directeurs unitaires opposés, on obtient ainsi a priori quatre valeurs, qui se réduisent en fait à deux, puisque
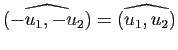 et
et
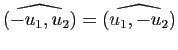 . Il faut donc identifier ces deux valeurs, ce qui se fait, ici encore, au moyen d'une relation d'équivalence. Cette relation consiste à identifier les angles
. Il faut donc identifier ces deux valeurs, ce qui se fait, ici encore, au moyen d'une relation d'équivalence. Cette relation consiste à identifier les angles
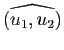 et
et
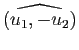 , ou encore un angle
, ou encore un angle 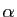 et l'angle
et l'angle
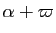 : deux angles sont donc en relation si et seulement si leur différence est 0 ou
: deux angles sont donc en relation si et seulement si leur différence est 0 ou 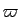 . L'addition des angles est compatible avec cette relation, ce qui permet de définir sur l'ensemble quotient
. L'addition des angles est compatible avec cette relation, ce qui permet de définir sur l'ensemble quotient 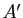 de
de  par cette relation d'équivalence une addition qui fait de
par cette relation d'équivalence une addition qui fait de 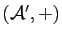 un groupe abélien, appelé groupe des angles de droites. Ce groupe n'est bien entendu rien d'autre que le groupe quotient du groupe abélien
un groupe abélien, appelé groupe des angles de droites. Ce groupe n'est bien entendu rien d'autre que le groupe quotient du groupe abélien 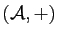 par son seul sous-groupe à deux éléments, constitué de l'angle nul et de l'angle plat. Il comporte lui-même un seul élément d'ordre 2, l'angle droit, qui est la classe des deux angles droits de vecteurs.
par son seul sous-groupe à deux éléments, constitué de l'angle nul et de l'angle plat. Il comporte lui-même un seul élément d'ordre 2, l'angle droit, qui est la classe des deux angles droits de vecteurs.
Mesure des angles
Rien de ce que nous avons fait jusqu'ici ne fait appel à l'orientation de  : on peut parfaitement définir les angles et écrire, par exemple, la relation de Chasles, sans avoir orienté le plan, et sans rien connaître non plus des fonctions trigonométriques. Par contre, dès qu'on veut mesurer les angles, l'orientation du plan joue un rôle essentiel. L'introduction de cette mesure des angles nécessite des outils d'analyse : il faut connaître les fonctions
: on peut parfaitement définir les angles et écrire, par exemple, la relation de Chasles, sans avoir orienté le plan, et sans rien connaître non plus des fonctions trigonométriques. Par contre, dès qu'on veut mesurer les angles, l'orientation du plan joue un rôle essentiel. L'introduction de cette mesure des angles nécessite des outils d'analyse : il faut connaître les fonctions 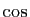 et
et 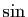 et leurs propriétés, ou, ce qui revient essentiellement au même, la fonction
et leurs propriétés, ou, ce qui revient essentiellement au même, la fonction
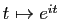 d'une variable réelle
d'une variable réelle 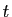 , en particulier le fait que cette fonction définit un homomorphisme du groupe additif
, en particulier le fait que cette fonction définit un homomorphisme du groupe additif
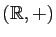 sur le groupe multiplicatif
sur le groupe multiplicatif
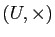 des nombres complexes de module 1, dont le noyau est le sous-groupe
des nombres complexes de module 1, dont le noyau est le sous-groupe
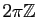 . On en déduit un isomorphisme naturel du groupe quotient
. On en déduit un isomorphisme naturel du groupe quotient
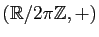 sur
sur
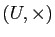 , et donc sur le groupe
, et donc sur le groupe 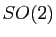 des matrices orthogonales positives d'ordre 2 : cet isomorphisme associe à la classe du réel
des matrices orthogonales positives d'ordre 2 : cet isomorphisme associe à la classe du réel 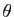 la matrice
la matrice
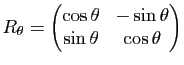 .
.
Or le choix d'une orientation du plan permet d'identifier une rotation vectorielle 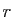 et une matrice de
et une matrice de 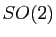 : on associe simplement à
: on associe simplement à 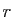 sa matrice dans n'importe quelle base orthonormée directe (il faut se souvenir que cette matrice ne dépend pas du choix d'une telle base). On obtient ainsi, par composition, un isomorphisme du groupe
sa matrice dans n'importe quelle base orthonormée directe (il faut se souvenir que cette matrice ne dépend pas du choix d'une telle base). On obtient ainsi, par composition, un isomorphisme du groupe
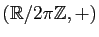 sur le groupe
sur le groupe 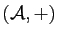 des angles de vecteurs, ce qui permet d'identifier un angle et sa mesure, qui est, par définition, l'élément de
des angles de vecteurs, ce qui permet d'identifier un angle et sa mesure, qui est, par définition, l'élément de
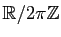 qui lui correspond par cet isomorphisme. On retombe ainsi sur la définition adoptée dans la première approche de la notion d'angle orienté de vecteurs.
qui lui correspond par cet isomorphisme. On retombe ainsi sur la définition adoptée dans la première approche de la notion d'angle orienté de vecteurs.
Cette mesure dépend de l'orientation : en effet, si une rotation vectorielle 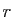 a comme matrice
a comme matrice 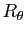 dans une base orthonormée directe, la matrice de
dans une base orthonormée directe, la matrice de 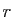 dans une base orthonormée indirecte est
dans une base orthonormée indirecte est
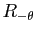 . Autrement dit, si un angle a pour mesure
. Autrement dit, si un angle a pour mesure 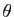 dans le plan orienté, et si on change l'orientation du plan, la mesure de l'angle devient
dans le plan orienté, et si on change l'orientation du plan, la mesure de l'angle devient 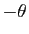 .
.
Si on veut mesurer les angles de droites, il faut factoriser l'homomorphisme de
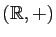 dans le groupe
dans le groupe 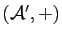 des angles de droites, de noyau
des angles de droites, de noyau
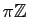 , ce qui revient à identifier des réels différant d'un multiple entier de
, ce qui revient à identifier des réels différant d'un multiple entier de 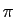 . La mesure d'un angle de droites est donc la classe d'équivalence d'un réel modulo
. La mesure d'un angle de droites est donc la classe d'équivalence d'un réel modulo 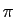 (cette mesure dépend, là encore, du choix d'une orientation).
(cette mesure dépend, là encore, du choix d'une orientation).
Angles dans l'espace
On ne peut, dans l'espace vectoriel euclidien de dimension 3, même orienté, définir la mesure d'un angle orienté de deux vecteurs, ou de deux droites. En effet l'orientation de l'espace n'induit pas d'orientation naturelle sur un plan de cet espace : on ne peut donc distinguer entre un angle et son opposé (par contre, la mesure de l'angle d'une rotation est bien définie, à condition d'avoir orienté l'axe de cette rotation : en effet une orientation de l'axe par le choix d'un vecteur directeur unitaire  induit automatiquement une orientation du plan vectoriel orthogonal à cet axe (une base orthonormée
induit automatiquement une orientation du plan vectoriel orthogonal à cet axe (une base orthonormée 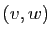 de ce plan est directe si la base
de ce plan est directe si la base 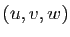 de l'espace est directe)). La notion la plus utile est donc ici celle d'angle géométrique de deux vecteurs unitaires, la mesure de l'angle de deux tels vecteurs
de l'espace est directe)). La notion la plus utile est donc ici celle d'angle géométrique de deux vecteurs unitaires, la mesure de l'angle de deux tels vecteurs  et
et  étant ici encore
étant ici encore
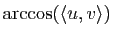 . Il n'y a bien entendu plus non plus de relation de Chasles pour ces angles.
. Il n'y a bien entendu plus non plus de relation de Chasles pour ces angles.
Groupe orthogonal en dimension 3
Dans cette partie,  est un espace vectoriel euclidien orienté de dimension 3.
est un espace vectoriel euclidien orienté de dimension 3.
Proposition 28
Toute transformation orthogonale  de
de  de déterminant +1 admet la valeur propre +1. L'espace propre associé est, si
de déterminant +1 admet la valeur propre +1. L'espace propre associé est, si  n'est pas l'identité, une droite vectorielle
n'est pas l'identité, une droite vectorielle 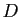 . Le plan vectoriel
. Le plan vectoriel 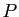 orthogonal à
orthogonal à 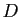 est stable par
est stable par  et la restriction de
et la restriction de  à ce plan est une rotation vectorielle de
à ce plan est une rotation vectorielle de 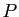 . La matrice de
. La matrice de  dans toute base orthonormée de
dans toute base orthonormée de  dont le premier vecteur
dont le premier vecteur  appartient à
appartient à 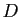 s'écrit
s'écrit
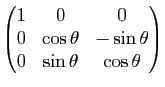 pour un réel
pour un réel 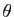 , unique modulo
, unique modulo 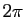 .
.
On dit alors que  est la rotation vectorielle d'axe
est la rotation vectorielle d'axe 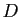 (orienté par le choix du vecteur unitaire
(orienté par le choix du vecteur unitaire  ) et d'angle
) et d'angle 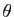 .
.
Démonstration : Soit  la matrice de
la matrice de  dans une base orthonormée directe de
dans une base orthonormée directe de  . De la relation
. De la relation
on déduit
d'où
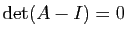 , ce qui montre que 1 est valeur propre de
, ce qui montre que 1 est valeur propre de  . Soit
. Soit  un vecteur propre unitaire de
un vecteur propre unitaire de  associé à la valeur propre 1, i.e. un vecteur unitaire fixe par
associé à la valeur propre 1, i.e. un vecteur unitaire fixe par  .
On vérifie que la matrice de
.
On vérifie que la matrice de  dans toute base orthonormée directe de
dans toute base orthonormée directe de  dont le premier vecteur est
dont le premier vecteur est  s'écrit alors sous la forme indiquée dans l'énoncé. La proposition en résulte.
s'écrit alors sous la forme indiquée dans l'énoncé. La proposition en résulte.
Si on change l'orientation de l'axe 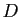 en prenant comme vecteur directeur
en prenant comme vecteur directeur 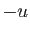 , l'angle
, l'angle 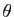 est changé en son opposé. La mesure de l'angle d'une rotation de l'espace dépend donc de l'orientation de son axe.
est changé en son opposé. La mesure de l'angle d'une rotation de l'espace dépend donc de l'orientation de son axe.
On remarque que l'angle géométrique d'une rotation s'obtient immédiatement à partir de la matrice de cette rotation : en effet, en reprenant les notations de la démonstration précédente, la trace de la matrice  est
est
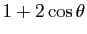 ; or la trace d'un endomorphisme ne dépend pas de la base (deux matrices semblables ont même trace) ; il en résulte que
; or la trace d'un endomorphisme ne dépend pas de la base (deux matrices semblables ont même trace) ; il en résulte que
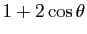 est la trace de la matrice de
est la trace de la matrice de  dans n'importe quelle base de
dans n'importe quelle base de  (éventuellement non orthonormée).
(éventuellement non orthonormée).
Pour déterminer le signe de l'angle d'une rotation vectorielle, on peut utiliser la proposition suivante :
Proposition 29
Si  est une rotation vectorielle qui n'est pas un demi-tour, d'axe orienté par le choix d'un vecteur directeur
est une rotation vectorielle qui n'est pas un demi-tour, d'axe orienté par le choix d'un vecteur directeur  , le signe de
, le signe de
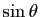 est celui de
est celui de
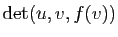 pour tout vecteur
pour tout vecteur  non colinéaire à
non colinéaire à  .
.
Démonstration : Soit 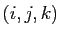 une base orthonormée directe telle que
une base orthonormée directe telle que
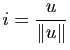 . La matrice de
. La matrice de  dans cette base est
dans cette base est
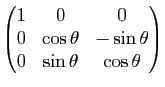 . Si
. Si  a pour composantes
a pour composantes 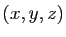 dans cette base, on a
dans cette base, on a
qui est du signe de
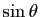 puisque
puisque
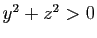 .
.
Proposition 30
Toute transformation orthogonale  de
de  de déterminant -1 admet la valeur propre -1. L'espace propre associé est, si
de déterminant -1 admet la valeur propre -1. L'espace propre associé est, si  est différente de
est différente de 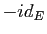 , une droite vectorielle
, une droite vectorielle 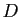 . Le plan vectoriel
. Le plan vectoriel 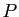 orthogonal à
orthogonal à 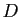 est stable par
est stable par  et la restriction de
et la restriction de  à ce plan est une rotation vectorielle de
à ce plan est une rotation vectorielle de 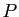 . Si cette rotation est l'identité de
. Si cette rotation est l'identité de 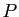 ,
,  est la réflexion de plan
est la réflexion de plan 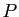 . Sinon,
. Sinon,  est le produit commutatif d'une rotation d'axe
est le produit commutatif d'une rotation d'axe 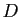 et de la réflexion de plan
et de la réflexion de plan 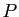 . La matrice de
. La matrice de  dans toute base orthonormée de
dans toute base orthonormée de  dont le premier vecteur
dont le premier vecteur  appartient à
appartient à 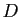 s'écrit dans tous les cas
s'écrit dans tous les cas
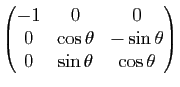 pour un réel
pour un réel 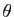 , unique modulo
, unique modulo 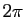 (
( est une réflexion si
est une réflexion si
 modulo
modulo 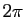 ,
, 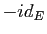 si
si
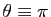 modulo
modulo 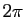 ).
).
Démonstration : Soit  la matrice de
la matrice de  dans une base orthonormée directe de
dans une base orthonormée directe de  . De la relation
. De la relation
on déduit
d'où
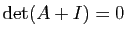 , ce qui montre que -1 est valeur propre de
, ce qui montre que -1 est valeur propre de  .
Soit
.
Soit  un vecteur propre unitaire de
un vecteur propre unitaire de  associé à la valeur propre -1.
On vérifie que la matrice de
associé à la valeur propre -1.
On vérifie que la matrice de  dans toute base orthonormée directe de
dans toute base orthonormée directe de  dont le premier vecteur est
dont le premier vecteur est  s'écrit alors sous la forme indiquée dans l'énoncé. La proposition en résulte.
s'écrit alors sous la forme indiquée dans l'énoncé. La proposition en résulte.
On dit, si  n'est pas une réflexion, que
n'est pas une réflexion, que  est une antirotation, ou encore une isométrie vectorielle gauche.
est une antirotation, ou encore une isométrie vectorielle gauche.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
 conserve le produit scalaire :
conserve le produit scalaire :
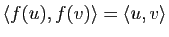 pour tout couple
pour tout couple
 ;
;
 conserve la norme :
conserve la norme :
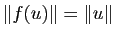 pour tout
pour tout 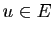 ;
;
 de toute base orthonormée de
de toute base orthonormée de  est une base orthonormée ;
est une base orthonormée ;
 dont l'image par
dont l'image par  est une base orthonormée ;
est une base orthonormée ;
 dans laquelle la matrice de
dans laquelle la matrice de  est orthogonale ;
est orthogonale ;
 dans toute base orthonormée de
dans toute base orthonormée de  est orthogonale.
est orthogonale.
![$\displaystyle = \dfrac12 \left[ \Vert f(u)+f(v)\Vert^2-\Vert f(u)\Vert^2-\Vert f(v)\Vert^2 \right]$](img203.gif)
![$\displaystyle = \dfrac12 \left[ \Vert f(u+v)\Vert^2-\Vert f(u)\Vert^2-\Vert f(v)\Vert^2 \right]$](img204.gif)
![$\displaystyle = \dfrac12 \left[ \Vert u+v\Vert^2-\Vert u\Vert^2-\Vert v\Vert^2 \right]$](img205.gif)
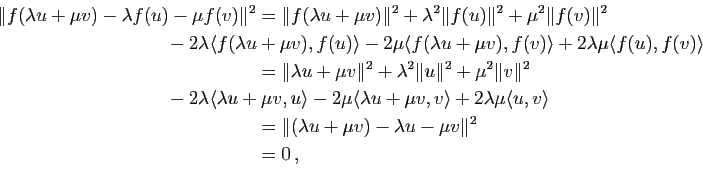
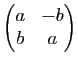
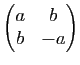
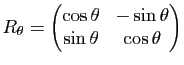
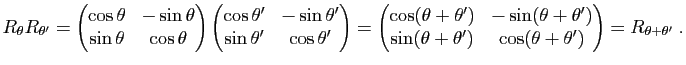
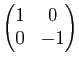
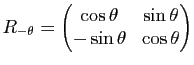

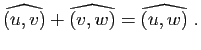
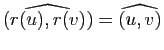
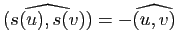



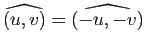
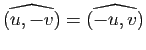
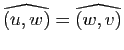
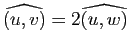
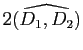
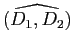
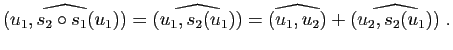
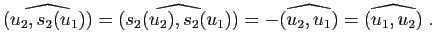
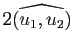
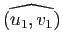
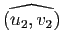
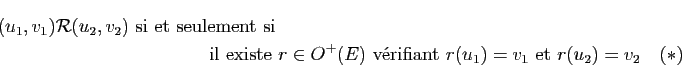
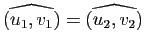
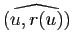
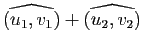

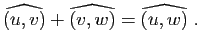
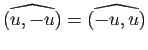

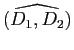
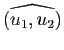
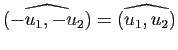
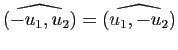
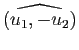
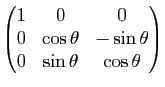
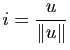
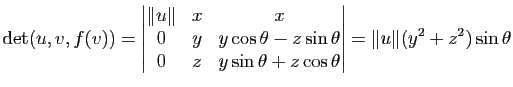
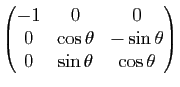
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales