Section : Espaces affines euclidiens
Avant : Espaces affines euclidiens
Après : Isométries, similitudes

Distance et orthogonalité

Définition 16   On appelle espace affine euclidien tout espace affine dont la direction est un espace vectoriel euclidien.

Dans toute cette section, $ E$ désignera un espace affine euclidien de dimension finie (souvent égale à 2 ou 3) de direction $ \overrightarrow{E}$. Les points de $ E$ seront désignés (sauf exception) par des lettres majuscules, les vecteurs de $ \overrightarrow{E}$ seront toujours notés avec des flèches pour les distinguer des points de $ E$. On notera $ \u \cdot \v$ le produit scalaire de deux vecteurs $ \vec u$ et $ \vec v$.

Proposition 39   Un espace affine euclidien est naturellement muni d'une distance $ d$, appelée distance euclidienne, définie par

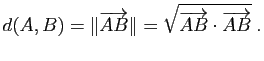
$\displaystyle d(A,B)=\Vert\vv{AB}\Vert=\sqrt{\vv{AB}\cdot \vv{AB}} \; .$

Cette distance vérifie l'inégalité triangulaire :

$\displaystyle \vert AB-AC\vert\leq BC \leq AB+AC$

pour tout triplet $ (A,B,C)$ de points de $ E$, et on a l'égalité $ BC=AB+AC$ si et seulement si $ A$ appartient au segment $ [BC]$.

Démonstration : Les propriétés $ d(A,B)=d(B,A)$ et $ d(A,B)=0$ si et seulement si $ A=B$ sont immédiates. L'inégalité triangulaire provient de l'inégalité triangulaire pour la norme euclidienne et de la relation de Chasles $ \vv{BC}=\vv{BA}+\vv{AC}$. On a égalité dans cette inégalité si et seulement si les vecteurs $ \vv{BA}$ et $ \vv{AC}$ sont directement proportionnels, i.e. si et seulement si $ A$ appartient au segment $ [BC]$.$ \square$

Conformément à un usage solidement établi, on notera systématiquement $ AB$ la distance $ d(A,B)$ de deux points $ A$ et $ B$.

Définition 17   Un repère cartésien $ (O,\e_1,\dots,\e_n)$ d'un espace affine euclidien $ E$ est dit orthonormé (ou orthonormal) si la base $ (e_1,\dots,e_n)$ de $ \overrightarrow{E}$ est orthonormée.

Un espace affine euclidien $ E$ est dit orienté si sa direction $ \overrightarrow{E}$ est un espace vectoriel euclidien orienté.

Définition 18   Deux sous-espaces affines sont dits orthogonaux si leurs directions sont des sous-espaces vectoriels orthogonaux.

Définition 19   Soit $ H$ un hyperplan d'un espace affine euclidien $ E$. On appelle vecteur normal à $ H$ tout vecteur non nul orthogonal à $ H$.

Proposition 40   Soit $ E$ un espace affine euclidien de dimension $ n$ rapporté à un repère orthonormé. L'hyperplan $ H$ passant par un point $ B$ de coordonnées $ (b_1,\dots,b_n)$ et de vecteur normal $ \n \, (a_1,\dots,a_n)$ admet l'équation $ a_1(x_1-b_1)+\dots +a_n(x_n-b_n)=0$.

Réciproquement si un hyperplan $ H$ admet l'équation $ a_1x_1+\dots a_n x_n +b=0$, alors le vecteur $ \n \, (a_1,\dots,a_n)$ est un vecteur normal à $ H$.

Démonstration : Pour démontrer la première assertion, il suffit d'écrire qu'un point $ M$ de $ E$ appartient à $ H$ si et seulement si $ \n \cdot \vv{BM}=0$. La seconde vient de ce que deux équations représentent un même hyperplan si et seulement si elles sont proportionnelles.$ \square$

Dans un plan affine euclidien, deux droites orthogonales sont toujours sécantes. Il n'en va pas de même dans l'espace de dimension 3. Deux droites sont dites perpendiculaires si elles sont orthogonales et sécantes.

Proposition 41   Soient $ D_1$ et $ D_2$ deux droites non parallèles de l'espace affine euclidien de dimension 3. Alors il existe une droite et une seule perpendiculaire à $ D_1$ et à $ D_2$. Cette droite est appelée perpendiculaire commune à $ D_1$ et $ D_2$ et ses points d'intersection $ A_1$ et $ A_2$ avec $ D_1$ et $ D_2$ pieds de la perpendiculaire commune. La distance $ A_1A_2$ réalise la distance minimale entre un point de $ D_1$ et un point de $ D_2$ :

$\displaystyle A_1A_2=\min \{ M_1M_2 \mid M_1 \in D_1,\, M_2\in D_2\}=d(D_1,D_2)$

et ce minimum n'est atteint que pour le couple $ (A_1,A_2)$.

Démonstration : Soient $ D_1$ et $ D_2$ deux droites non parallèles, $ M_1$ (resp. $ M_2$) un point de $ D_1$ (resp. $ D_2$), $ \v_1$ (resp. $ \v_2$) un vecteur directeur de $ D_1$ (resp. $ D_2$). Si une droite $ \Delta$ est perpendiculaire à $ D_1$ et $ D_2$, tout vecteur directeur de cette droite est orthogonal à $ \v_1$ et $ \v_2$, donc colinéaire à $ \w=\v_1 \wedge \v_2$, qui n'est pas nul puisque $ \v_1$ et $ \v_2$ ne sont pas colinéaires. La droite $ \Delta$ est donc incluse dans le plan $ P_1$ passant par $ M_1$ et de vecteurs directeurs $ \v_1$ et $ w$, puisqu'elle rencontre $ D_1$. De même, $ \Delta$ est incluse dans le plan $ P_2$ passant par $ M_2$ et de vecteurs directeurs $ \v_2$ et $ w$. Ces deux plans ne peuvent être parallèles, sinon le système $ (\v_1,\v_2,\w)$ serait lié, puisque ces trois vecteurs appartiendraient à un même plan vectoriel. Leur intersection est donc une droite et $ \Delta$ ne peut être que cette droite, ce qui prouve l'unicité de la perpendiculaire commune.

Pour montrer l'existence, il suffit de vérifier que l'intersection $ \Delta$ des deux plans $ P_1$ et $ P_2$ est perpendiculaire à $ D_1$ et $ D_2$ : elle leur est orthogonale, puisque $ w$ en est un vecteur directeur, et elle rencontre $ D_1$, puisqu'elle est coplanaire avec $ D_1$ (ces deux droites sont incluses dans $ P_1$) et non parallèle à $ D_1$ ; elle rencontre $ D_2$ pour des raisons analogues.

Soient $ A_1$ et $ A_2$ les pieds de la perpendiculaire commune. Pour tout point $ M_1$ de $ D_1$ et tout point $ M_2$ de $ D_2$, on a $ \vv{M_1M_2}=\vv{M_1A_1}+\vv{A_1A_2}+\vv{A_2M_2}$ d'après la relation de Chasles. Mais les vecteurs $ \vv{A_1A_2}$ et $ \vv{M_1A_1}+\vv{A_2M_2}$ étant orthogonaux, on en déduit $ M_1M_2^2=A_1A_2^2+\Vert\vv{M_1A_1}+\vv{A_2M_2}\Vert^2$, d'où $ M_1M_2 \geq A_1A_2$. L'égalité n'est obtenue que pour $ \vv{M_1A_1}+\vv{A_2M_2}=\0$ ; les droites $ D_1$ et $ D_2$ n'étant pas parallèles, cette égalité implique $ \vv{M_1A_1}=\vv{A_2M_2}=\0$.$ \square$

Deux droites parallèles et distinctes de l'espace définissent un plan et admettent une infinité de perpendiculaires communes, toutes parallèles entre elles.


Dans l'espace affine euclidien de dimension 3, une droite et un plan orthogonaux sont toujours sécants (on dit indifféremment que la droite est orthogonale ou perpendiculaire au plan). Deux plans d'un tel espace ne peuvent être orthogonaux : en effet la somme des dimensions de deux sous-espace affines orthogonaux est toujours inférieure ou égale à la dimension de l'espace.

Définition 20   Dans un espace affine euclidien de dimension 3, deux plans sont dits perpendiculaires si leurs vecteurs normaux sont orthogonaux.

Proposition 42   Deux plans d'un espace affine euclidien de dimension 3 sont perpendiculaires si et seulement si un de ces plans contient une droite orthogonale à l'autre.

Démonstration : Soient $ P_1$ et $ P_2$ deux plans de l'espace, $ \n_1$ et $ \n_2$ des vecteurs normaux à ces plans. Supposons que $ P_1$ contienne une droite $ D$ orthogonale à $ P_2$. Le vecteur $ \n_2$ est alors un vecteur directeur de $ D$ et il est orthogonal à $ \n_1$, puisque $ D$ est incluse dans $ P_1$.

Réciproquement, si $ \n_1$ et $ \n_2$ sont orthogonaux, pour tout point $ M$ de $ P_1$, la droite passant par $ M$ de vecteur directeur $ \n_2$ est orthogonale à $ P_2$ et incluse dans $ P_1$.$ \square$

Corollaire 7   Soient $ P_1$ et $ P_2$ deux plans de l'espace. Si $ P_1$ contient une droite orthogonale à $ P_2$, alors $ P_2$ contient une droite orthogonale à $ P_1$.

Projection orthogonale, problèmes de distances

Définition 21   Soit $ E$ un espace affine euclidien et $ F$ un sous-espace affine de $ E$. On appelle projection orthogonale sur $ F$ la projection sur $ F$ dans la direction $ F^\perp$.

Toute projection orthogonale de $ E$ est une application affine dont la partie linéaire est un endomorphisme symétrique de $ \overrightarrow{E}$. La distance entre deux points de $ E$ est toujours supérieure à la distance entre leurs projetés.

Proposition 43   Soit $ E$ un espace affine euclidien et $ F$ un sous-espace affine de $ E$. Alors pour tout point $ M$ de $ E$, le projeté orthogonal $ H$ de $ M$ sur $ E$ est l'unique point de $ F$ réalisant la distance de $ M$ à $ F$ :

$\displaystyle MH=\min\{ M N \mid N\in F\}=d(M,F)\; .$

Démonstration : La proposition résulte immédiatement de la relation de Pythagore : $ MN^2=MH^2+HN^2$ pour tout point $ N$ de $ F$, puisque les vecteurs $ \vv{MH}$ et $ \vv{HN}$ sont orthogonaux.$ \square$

Proposition 44   Soit, dans un espace affine euclidien $ E$ de dimension $ n$, $ H$ un hyperplan défini par un point $ B$ et un vecteur normal $ \vec n$. Alors la distance de $ M$ à $ H$ est donnée par

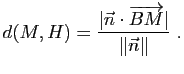
$\displaystyle d(M,H)=\dfrac{\vert \n \cdot \vv{BM}\vert}{\Vert\n\Vert} \; .$

Si $ E$est rapporté à un repère orthonormé et si $ M$ a pour coordonnées $ (x_1,\dots,x_n)$ et $ H$ comme équation $ a_1 x_1+\cdots a_nx_n+b=0$, cette distance est donnée par

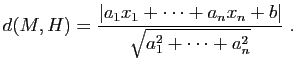
$\displaystyle d(M,H)=\dfrac{\vert a_1x_1+\dots+a_nx_n+b\vert}{\sqrt{a_1^2+\dots+a_n^2}} \; .$

Démonstration : Soit $ M'$ le projeté orthogonal de $ M$ sur $ H$. La distance de $ M$ à $ H$ est égale à $ MM'$ et

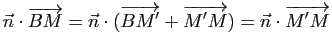
$\displaystyle \n \cdot \vv{BM}=\n \cdot (\vv{BM'}+\vv{M'M})=\n \cdot \vv{M'M}$

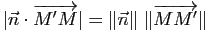puisque les vecteurs $ \vec n$ et $ \vv{BM'}$ sont orthogonaux. Les vecteurs $ \vec n$ et $ \vv{MM'}$ étant colinéaires, on a $ \vert \n \cdot \vv{M'M} \vert = \Vert\n\Vert \; \Vert\vv{MM'}\Vert$, d'où le résultat.

Si $ H$ a comme équation $ a_1 x_1+\cdots a_nx_n+b=0$ dans un repère orthonormé, le vecteur $ \vec n$ de composantes $ (a_1,\dots,a_n)$ est un vecteur normal de $ H$. Si $ B$ de coordonnées $ (b_1,\dots,b_n)$ est un point de $ H$, on a

$\displaystyle \n \cdot \vv{BM}=a_1(x_1-b_1)+\dots +a_n(x_n-b_n)=a_1x_1+\dots + a_n x_n +b$

puisque le point $ B$ appartenant à $ H$ vérifie $ a_1b_1+\dots+a_nb_n+b=0$.$ \square$

On obtient ainsi la distance d'un point à une droite dans le plan et la distance d'un point à un plan dans l'espace. La distance d'un point à une droite dans l'espace est donnée par la proposition suivante.

Proposition 45   Soit, dans un espace affine euclidien de dimension 3, $ D$ une droite définie par un point $ A$ et un vecteur directeur $ \vec v$. La distance d'un point $ M$ à $ D$ est donnée par

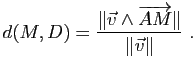
$\displaystyle d(M,D)=\dfrac{\Vert\v \wedge \vv{AM}\Vert}{\Vert \v \Vert} \; .$

Démonstration : Soit $ M'$ le projeté orthogonal de $ M$ sur $ H$. La distance de $ M$ à $ D$ est égale à $ MM'$ et

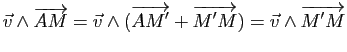
$\displaystyle \v \wedge \vv{AM}=\v \wedge (\vv{AM'}+\vv{M'M})=\v \wedge \vv{M'M}$

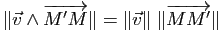puisque les vecteurs $ \vec v$ et $ \vv{AM'}$ sont colinéaires. Les vecteurs $ \vec v$ et $ \vv{MM'}$ étant orthogonaux, on a $ \Vert \v \wedge \vv{M'M} \Vert = \Vert\v\Vert \; \Vert\vv{MM'}\Vert$, d'où le résultat.$ \square$

Symétrie orthogonale, réflexion, hyperplan médiateur

Définition 22   Soit $ E$ un espace affine euclidien et $ F$ un sous-espace affine de $ E$. On appelle symétrie orthogonale par rapport à $ F$ la symétrie par rapport à $ F$ dans la direction $ F^\perp$.

On appelle réflexion toute symétrie orthogonale par rapport à un hyperplan.

Une réflexion est donc, dans le plan, une symétrie orthogonale par rapport à une droite et, dans l'espace, une symétrie orthogonale par rapport à un plan.

Proposition 46   L'ensemble des points d'un espace affine euclidien $ E$ équidistants de deux points $ A$ et $ B$ distincts est l'hyperplan orthogonal à la droite $ (AB)$ passant par le milieu $ I$ de $ [AB]$. Cet hyperplan est appelé hyperplan médiateur de $ [AB]$ (médiatrice si $ \dim(E)=2$, plan médiateur si $ \dim(E)=3$).

Les deux ensembles $ \{M\in E \mid MA>MB\}$ et $ \{M\in E \mid MA<MB\}$ (resp. $ \{M\in E \mid MA \geq MB\}$ et $ \{M\in E \mid MA \leq MB\}$) sont les deux demi-espaces ouverts (resp. fermés) délimités par cet hyperplan.

Démonstration : La première partie de la proposition résulte de l'égalité

$\displaystyle MA^2-MB^2=(\vv{MA}-\vv{MB})\cdot (\vv{MA}+\vv{MB})=2 \; \vv{AB} \cdot \vv{IM} \; .$

La seconde partie s'obtient en remplaçant les égalités par des inégalités.$ \square$

Proposition 47   Soient $ A$ et $ B$ deux points distincts d'un espace affine euclidien $ E$. Il existe alors une réflexion et une seule échangeant ces deux points. Son hyperplan est l'hyperplan médiateur de $ [AB]$.

Démonstration : Soit $ s$ une réflexion d'hyperplan $ H$ vérifiant $ s(A)=B$ (on a alors $ s(B)=A$ puisque $ s\circ s=id_E$). Comme $ s$ est affine, elle laisse fixe le milieu $ I$ de $ [AB]$, qui appartient donc à $ H$. Par ailleurs, $ H$ est orthogonal à la droite $ (AB)$. C'est donc l'hyperplan médiateur de $ [AB]$.

Réciproquement, si $ H$ est l'hyperplan médiateur de $ [AB]$, la droite $ (AB)$ est orthogonale à $ H$ en $ I$ et la symétrie orthogonale par rapport à $ H$ échange les points $ A$ et $ B$.$ \square$

Projection sur un convexe fermé, séparation de convexes

Proposition 48   Soit $ C$ un convexe fermé non vide d'un espace affine euclidien $ E$. Pour tout point $ M$ de $ E$, il existe un unique point $ P$ de $ C$ vérifiant $ MP=d(M,C)=\inf\{MQ\mid Q\in C\}$.

Ce point $ P$ est l'unique point de $ C$ vérifiant $ \vv{PM}\cdot\vv{PQ}\leq 0$ pour tout point $ Q$ de $ C$.

L'application $ p$ qui à $ M$ associe $ P$ est 1-lipschitzienne : $ p(M)p(N)\leq MN$ pour tout couple $ (M,N)$ de points de $ E$.

On l'appelle projection sur le convexe $ C$.

\includegraphics[width=0.5\textwidth]{convexe}

Démonstration : Soit $ M$ un point de $ E$ et $ A$ un point de $ C$. L'intersection de $ C$ et de la boule fermée de centre $ M$ et de rayon $ MA$ est un convexe compact de $ E$ et la fonction qui à tout point $ P$ de $ E$ associe la distance $ MP$ est continue sur ce compact. Elle y atteint donc son minimum, qui est aussi le minimum de la distance $ MP$ pour $ P$ dans $ C$.

Supposons que ce minimum $ d$ soit atteint en deux points distincts $ P_1$ et $ P_2$ de $ C$. Le milieu $ I$ de $ [P_1P_2]$ appartiendrait à $ C$, puisque $ C$ est convexe, et vérifierait

$\displaystyle 2 \, d^2=MP_1^2+MP_2^2=2 \, MI^2 + 2 \, IP_1^2$

par la relation de la médiane, d'où $ MI<d$, ce qui contredit l'hypothèse. Le minimum est donc atteint en un point et un seul.

Pour tout point $ Q$ de $ C$, le segment $ [PQ]$ est inclus dans $ C$, puisque $ C$ est convexe. On a donc $ MP^2\leq MR^2$ pour tout point $ R$ de ce segment. Mais $ R$ appartient au segment $ [MQ]$ si et seulement si il existe un réel $ t\in [0,1]$ tel que $ \vv{PR}=t\vv{PQ}$. On a donc $ MP^2 \leq (\vv{MP}+t\vv{PQ})^2$ pour tout $ t\in [0,1]$, soit encore $ 0 \leq 2t\vv{MP}\cdot\vv{PQ}+t^2 PQ^2$ pour tout $ t\in [0,1]$. En divisant par $ t$ et en faisant tendre $ t$ vers 0, on obtient $ 0 \leq \vv{MP}\cdot\vv{PQ}$.

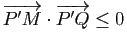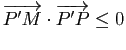Si un point $ P'$ de $ C$ vérifie $ \vv{P'M}\cdot\vv{P'Q}\leq 0$ pour tout point $ Q$ de $ C$, il vérifie en particulier $ \vv{P'M}\cdot\vv{P'P}\leq 0$, soit encore 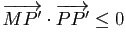$ \vv{MP'}\cdot\vv{PP'}\leq 0$. En ajoutant cette inégalité à l'inégalité 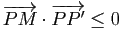$ \vv{PM}\cdot\vv{PP'}\leq 0$, on obtient 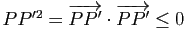$ PP'^2=\vv{PP'}\cdot\vv{PP'}\leq 0$, d'où $ P'=P$.

Soient $ M$ et $ N$ deux points de $ E$, $ P=p(M)$ et $ Q=p(N)$ leurs projetés sur $ C$. On a $ \vv{MP}\cdot \vv{PQ}\geq 0$ et $ \vv{PQ}\cdot \vv{QN}\geq 0$ d'après la propriété précédente. Il en résulte

$\displaystyle MN^2$ $\displaystyle =(\vv{MP}+\vv{PQ}+\vv{QN})^2$    
  $\displaystyle =PQ^2+(\vv{MP}+\vv{QN})^2+2 \, \vv{MP}\cdot \vv{PQ}+2\, \vv{PQ}\cdot\vv{QN}$    
  $\displaystyle \geq PQ^2$    

d'où $ PQ\leq MN$.$ \square$

Remarque : L'application $ p$ définie dans cette proposition est une projection au sens où elle vérifie $ p\circ p=p$ (tout point de $ C$ est son propre projeté). Dans le cas où $ C$ est un sous-espace affine de $ E$, la projection $ p$ sur le convexe $ C$ n'est autre que la projection orthogonale sur $ C$ définie précédemment. C'est le seul cas où $ p$ soit affine, puisque l'image de $ E$ par une application affine est un sous-espace affine et que l'image de $ p$ est $ C$.

Corollaire 8   Soit $ C$ un convexe fermé non vide d'un espace affine euclidien $ E$. Pour tout point $ M$ de $ E$ n'appartenant pas à $ C$, il existe un hyperplan affine $ H$ de $ E$ séparant strictement $ M$ de $ C$, i.e. tel que $ M$ appartienne à l'un des deux demi-espaces ouverts délimités par $ H$ et que $ C$ soit contenu dans l'autre.

Démonstration : Soit $ P$ le projeté de $ M$ sur $ C$, $ I$ le milieu du segment $ [MP]$ et $ H$ l'hyperplan médiateur de $ [MP]$. On a, pour tout point $ Q$ de $ C$

$\displaystyle \vv{IP}\cdot \vv{IQ}=\vv{IP}\cdot (\vv{IP}+\vv{PQ})=IP^2+\vv{IP}\cdot \vv{PQ} \geq IP^2>0$

et

$\displaystyle \vv{IP}\cdot\vv{IM}=-IP^2 <0$

ce qui montre que $ M$ appartient à un des deux demi-espaces ouverts délimités par $ H$ et que $ C$ est inclus dans l'autre.$ \square$

Corollaire 9   Tout convexe fermé d'un espace affine euclidien est l'intersection des demi-espaces ouverts qui le contiennent.

Démonstration : Tout convexe fermé $ C$ est clairement inclus dans l'intersection des demi-espaces ouverts qui le contiennent. Si un point $ M$ n'appartient pas à $ C$, il existe un demi-espace ouvert contenant $ C$ et pas $ M$.$ \square$

On démontrerait de même, en considérant le couple $ (M,N)$ de points minimisant la distance d'un point de $ C_1$ à un point de $ C_2$ et l'hyperplan médiateur de $ [MN]$, le corollaire suivant :

Corollaire 10   Soient $ C_1$ et $ C_2$ deux convexes compacts disjoints d'un espace affine euclidien $ E$. Il existe un hyperplan $ H$ de $ E$ qui sépare strictement $ C_1$ de $ C_2$, i.e. tel que $ C_1$ soit inclus dans l'un des deux demi-espaces ouverts délimités par $ H$ et $ C_2$ dans l'autre.

Remarque : Ces corollaires ne font pas appel à la structure euclidienne de l'espace. Tout espace affine de dimension finie pouvant être muni d'une structure euclidienne, ils sont vrais pour tout espace affine réel.

Sphères

Définition 23   Soit $ E$ un espace affine euclidien, $ \Omega$ un point de $ E$ et $ R$ un réel positif. On appelle sphère de centre $ \Omega$ et de rayon $ R$ l'ensemble

$\displaystyle S(\Omega,R)=\{ M \in E \mid \Omega M=R\}$

des points de $ E$ dont la distance à $ \Omega$ est égale à $ R$ et boule fermée (resp. boule ouverte) de centre $ \Omega$ et de rayon $ R$ l'ensemble des points de $ E$ dont la distance à $ \Omega$ est inférieure (resp. strictement inférieure) à $ R$.

Proposition 49   Soit $ E$ un espace affine euclidien de dimension $ n$ rapporté à un repère orthonormé . La sphère de centre $ \Omega$ de coordonnées $ (a_1,\dots,a_n)$ et de rayon $ R$ a pour équation cartésienne

$\displaystyle (x_1-a_1)^2+\dots+(x_n-a_n)^2=R^2$

soit encore

$\displaystyle x_1^2+\dots+x_n^2-2\, a_1x_1-\dots-2\, a_nx_n+d=0$

en posant $ d=a_1^2+\dots+a_n^2-R^2$.

Réciproquement, une équation de cette forme est celle d'une sphère si $ a_1^2+\dots+a_n^2-d\geq 0$. Si $ a_1^2+\dots+a_n^2-d=0$, cette sphère est réduite à un point. Si $ a_1^2+\dots+a_n^2-d < 0$, l'ensemble des points la vérifiant est vide.

Définition 24   Deux points $ A$ et $ A'$ d'une sphère $ S$ de centre $ \Omega$ sont dits diamétralement opposés sur $ S$ s'ils sont symétriques par rapport à $ \Omega$. On dit alors que $ [AA']$ est un diamètre de la sphère $ S$.

Proposition 50   Un point $ M$ appartient à la sphère de diamètre $ [AA']$ si et seulement si $ \vv{MA}\cdot \vv{MA'}=0$.

Démonstration : Soit $ \Omega$ le centre de la sphère, i.e. le milieu de $ [AA']$, et $ R$ son rayon. Alors

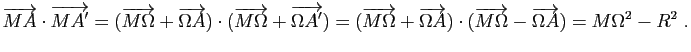
$\displaystyle \vv{MA}\cdot\vv{MA'}=(\vv{M\Omega}+\vv{\Omega A})\cdot(\vv{M\Omeg... ...\vv{M\Omega}+\vv{\Omega A})\cdot(\vv{M\Omega}-\vv{\Omega A})=M\Omega^2-R^2 \; .$

La proposition en découle.$ \square$

Proposition 51   L'intersection d'une sphère de centre $ \Omega$ et de rayon $ R$ avec un hyperplan $ H$ est :

Démonstration : Pour tout point $ M$ de $ H$, on a $ \Omega M^2=\Omega \Omega'^2+\Omega'M^2$ (relation de Pythagore) puisque les vecteurs $ \vv{\Omega\Omega'}$ et $ \vv{\Omega'M}$ sont orthogonaux, et $ \Omega\Omega'=d(\Omega,H)$.$ \square$

Dans le plan, l'intersection d'une droite et d'un cercle est donc constituée de 2, 1 ou 0 points. Dans l'espace de dimension 3, l'intersection d'une sphère et d'un plan est soit un cercle, soit un point, soit vide.

Définition 25   Un hyperplan $ H$ est dit tangent à une sphère $ S$ au point $ M$ si $ S\cap H=\{M\}$.

Corollaire 11   Par tout point $ M$ d'une sphère $ S$ de centre $ \Omega$, il passe un et un seul hyperplan tangent à cette sphère, qui est l'hyperplan orthogonal en $ M$ à la droite $ (\Omega M)$.

Démonstration : La distance de $ \Omega$ à un hyperplan $ H$ passant par $ M$ est strictement inférieure au rayon de $ S$, sauf si $ H$ est orthogonal à $ (\Omega M)$, auquel cas elle lui est égale.$ \square$

Les deux propositions suivantes sont énoncées pour un espace affine euclidien de dimension 3, mais elles se généralisent immédiatement en dimension quelconque.

Proposition 52   Intersection de deux sphères

L'intersection de deux sphères de centres respectifs $ \Omega$ et $ \Omega'$ distincts et de rayons respectifs $ R$ et $ R'$ est :

Démonstration : On commence par remarquer que l'intersection des deux sphères d'équations $ x_1^2+\dots+x_n^2-2\, a_1x_1-\dots-2\, a_nx_n+d=0$ et $ x_1^2+\dots+x_n^2-2\, a'_1x_1-\dots-2\, a'_nx_n+d'=0$ est aussi celle de l'une de ces sphères et de l'hyperplan d'équation $ 2\, (a_1-a'_1)x_1+\dots+2\, (a_n-a'_n)x_n+d-d'=0$ orthogonal à la droite $ (\Omega\Omega')$.$ \square$

La proposition suivante découle de la précédente et de l'inégalité triangulaire.

Proposition 53   Positions relatives de deux sphères

Soient $ S$ et $ S'$ deux sphères de centres distincts $ \Omega$ et $ \Omega'$ et de rayons respectifs $ R$ et $ R'$ et $ d=\Omega\Omega'$ la distance entre leurs centres. La position relative des deux sphères est alors donnée par l'un des cinq cas suivants :


Section : Espaces affines euclidiens
Avant : Espaces affines euclidiens
Après : Isométries, similitudes


         © UJF Grenoble, 2011                              Mentions légales