Le but de cette section est d'étudier les variations d'une fonction
 de
de
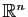 dans
dans
 , et en particulier de déterminer les
points de l'espace où elle atteint son maximum et son minimum. Afin
de mieux visualiser les notions introduites, nous nous plaçons en
dimension
, et en particulier de déterminer les
points de l'espace où elle atteint son maximum et son minimum. Afin
de mieux visualiser les notions introduites, nous nous plaçons en
dimension 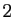 . La fonction
. La fonction
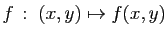 se représente par
la surface d'équation
se représente par
la surface d'équation 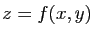 dans l'espace. Nous commençons
par la notion de dérivée directionnelle.
dans l'espace. Nous commençons
par la notion de dérivée directionnelle.
Pour comprendre cette définition, considérons la fonction 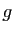 de
de
 dans
dans
 , qui à
, qui à 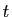 associe :
associe :
Elle définit une courbe sur la surface d'équation 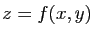 ,
au-dessus de la droite
,
au-dessus de la droite
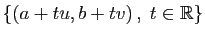 (voir figure
6). On dérive cette fonction par rapport à
(voir figure
6). On dérive cette fonction par rapport à 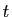 comme une fonction composée :
comme une fonction composée :
Soit en 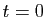 :
:
La dérivée directionnelle décrit les variations de
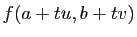 autour de
autour de 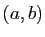 ,
dans la direction du vecteur
,
dans la direction du vecteur 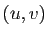 .
.
Figure 6:
Dérivée directionnelle.
|
|
La direction selon laquelle la croissance de la surface est la plus
forte est celle du gradient de la fonction. À titre d'exemple, nous
avons représenté sur la figure 7 quelques
valeurs du gradient de la fonction 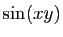 . Pour comparaison, nous
avons mis à côté une représentation de la fonction par niveaux
de gris : au lieu de la surface
. Pour comparaison, nous
avons mis à côté une représentation de la fonction par niveaux
de gris : au lieu de la surface
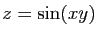 (figure 4),
les valeurs de la fonction sont symbolisées par des niveaux de gris,
d'autant plus clairs que les valeurs sont plus fortes. Les points blancs
sont des maxima de la fonction, et les points noirs des minima. On
constate que le gradient, s'il est non nul,
est toujours orienté vers le haut, dans la
direction de la «ligne de plus grande pente».
(figure 4),
les valeurs de la fonction sont symbolisées par des niveaux de gris,
d'autant plus clairs que les valeurs sont plus fortes. Les points blancs
sont des maxima de la fonction, et les points noirs des minima. On
constate que le gradient, s'il est non nul,
est toujours orienté vers le haut, dans la
direction de la «ligne de plus grande pente».
Figure:
Représentation par niveaux de gris de
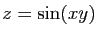 et champ
de gradient correspondant.
et champ
de gradient correspondant.
|
|
Sur la figure 7, on observe que le gradient est nul
pour les maxima et les minima. Définissons d'abord la notion de
maximum et minimum local.
Définition 9
Soit 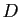 un domaine ouvert de
un domaine ouvert de
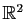 ,
,  une fonction
définie sur
une fonction
définie sur 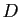 , et
, et 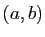 un point de
un point de 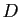 .
On dit que
.
On dit que  admet un maximum (respectivement un minimum)
local en
admet un maximum (respectivement un minimum)
local en 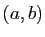 , s'il existe
, s'il existe
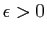 tel que
tel que
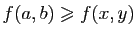 (respectivement
(respectivement
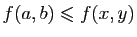 ),
pour tout
),
pour tout 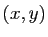 tel que
tel que
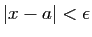 et
et
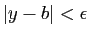 .
.
Démonstration : Si  admet un extremum (maximum ou minimum) local en
admet un extremum (maximum ou minimum) local en 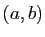 alors
il en est de même si on restreint
alors
il en est de même si on restreint  à la direction
à la direction
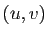 autour de
autour de 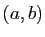 . La dérivée de la fonction (de
. La dérivée de la fonction (de 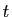 )
)
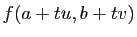 doit donc être nulle en
doit donc être nulle en 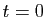 . Donc :
. Donc :
Mais les dérivées directionnelles ne peuvent être nulles dans
toutes les directions que si le gradient lui même est nul. Les points du plan où le gradient de
Les points du plan où le gradient de  s'annule sont les
points critiques de
s'annule sont les
points critiques de  .
La nullité du gradient n'est qu'une
condition nécessaire pour qu'un point soit un extremum. Rappelons
tout d'abord quelle est la situation pour les fonctions d'une
variable, deux fois continûment dérivable.
Si la fonction
.
La nullité du gradient n'est qu'une
condition nécessaire pour qu'un point soit un extremum. Rappelons
tout d'abord quelle est la situation pour les fonctions d'une
variable, deux fois continûment dérivable.
Si la fonction
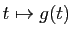 admet un maximum ou un minimum
local en
admet un maximum ou un minimum
local en 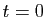 alors
alors 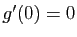 . Réciproquement :
. Réciproquement :
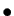
- Si
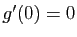 et si
et si
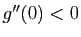 , alors 0 est un maximum local pour
, alors 0 est un maximum local pour 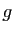 .
.
- Si
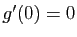 et si
et si
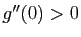 , alors 0 est un minimum local pour
, alors 0 est un minimum local pour 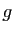 .
.
Revenons alors à une fonction de 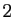 variables, que nous supposons
deux fois continûment différentiable. Examinons cette
fonction dans la direction
variables, que nous supposons
deux fois continûment différentiable. Examinons cette
fonction dans la direction 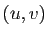 autour de
autour de 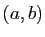 .
.
Le point 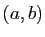 sera un maximum de
sera un maximum de  si 0 est un maximum pour
si 0 est un maximum pour
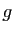 , quelle que soit la direction
, quelle que soit la direction 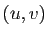 .
Calculons la dérivée seconde de
.
Calculons la dérivée seconde de 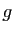 :
:
Donc en 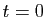 :
:
Cette expression peut s'écrire sous la forme matricielle suivante,
qui fait intervenir la matrice hessienne de  .
.
Il se trouve que, comme pour toute matrice
symétrique réelle,
il existe une matrice orthogonale
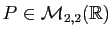 (vérifiant
(vérifiant
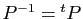 ) et deux réels
) et deux réels 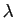 et
et 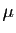 tels que :
tels que :
Les réels 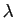 et
et 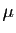 sont les valeurs propres de la
matrice hessienne. Pour les calculer, il suffit de connaître
leur somme, qui est la trace de la matrice hessienne, et leur produit,
qui est son déterminant.
sont les valeurs propres de la
matrice hessienne. Pour les calculer, il suffit de connaître
leur somme, qui est la trace de la matrice hessienne, et leur produit,
qui est son déterminant.
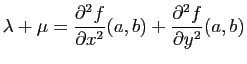
et
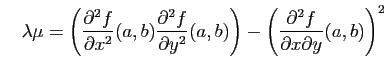
On résoud alors l'équation du second degré dont 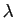 et
et 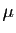 sont solution.
Posons :
sont solution.
Posons :
La dérivée seconde de 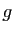 en 0 s'écrit :
en 0 s'écrit :
Le signe de 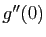 dépend donc des signes de
dépend donc des signes de 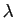 et
et 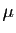 .
.
- Si
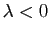 et
et 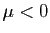 , alors
, alors 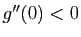 quelle que soit la
direction
quelle que soit la
direction 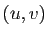 , donc le point
, donc le point 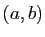 est un maximum local pour
est un maximum local pour  .
.
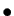
- Si
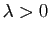 et
et 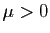 , alors
, alors 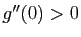 quelle que soit la
direction
quelle que soit la
direction 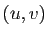 , donc le point
, donc le point  est un minimum local pour
est un minimum local pour  .
.
- Si
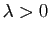 et
et 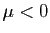 , alors
, alors 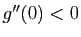 dans la direction
dans la direction
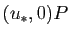 , et
, et 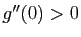 dans la direction
dans la direction 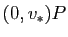 . Dans ce cas
on dit que le point
. Dans ce cas
on dit que le point 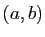 est un point selle pour
est un point selle pour  .
.
Les trois cas sont illustrés sur la figure 8.
Figure 8:
Maximum, minimum et point selle pour une fonction de
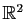 dans
dans
 .
.
|
|
Voici un exemple.
Le gradient et la matrice hessienne au point 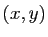 sont :
sont :
Le gradient s'annule en 4 points dans le plan. Nous les donnons avec
les valeurs propres de la matrice hessienne et la nature du point.
L'étude précédente se généralise aux fonctions de
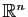 dans
dans
 .
.
Théorème 6
Soit 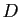 un domaine ouvert de
un domaine ouvert de
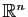 ,
,  une fonction deux fois
continûment différentiable sur
une fonction deux fois
continûment différentiable sur 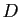 et
et 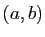 un point de
un point de 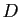 .
Notons
.
Notons  le gradient et
le gradient et 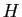 la matrice hessienne de
la matrice hessienne de  au point
au point 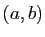 .
.
- Si
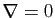 et si
et si
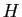 a toutes ses valeurs propres strictement négatives,
alors
a toutes ses valeurs propres strictement négatives,
alors 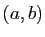 est un maximum local pour
est un maximum local pour  .
.
- Si
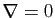 et si
et si
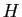 a toutes ses valeurs propres strictement positives,
alors
a toutes ses valeurs propres strictement positives,
alors 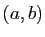 est un minimum local pour
est un minimum local pour  .
.
Les valeurs propres de 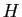 sont les racines du polynôme
sont les racines du polynôme 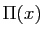 , où
, où
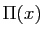 est le déterminant de la matrice
est le déterminant de la matrice 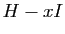 ,
, 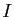 étant la matrice
indentité de taille
étant la matrice
indentité de taille 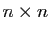 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
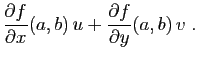
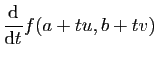
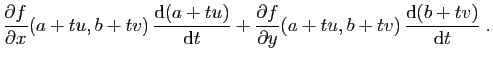
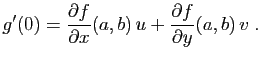
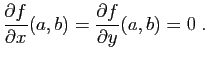
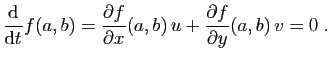
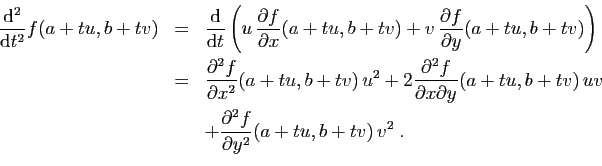
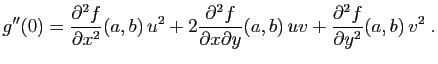
![\begin{displaymath}
(u,v)
\left(
\begin{array}{cc}
\frac{\partial^2 f}{\partial...
...) H
\left(
\begin{array}{c}
u [2ex]
v
\end{array}\right)\;.
\end{displaymath}](img179.gif)
![\begin{displaymath}
H
= P
\left(
\begin{array}{cc}
\lambda&0 [2ex]
0&\mu
\end{array}\right)
P^{-1}\;.
\end{displaymath}](img183.gif)
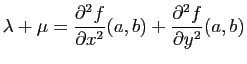 et
et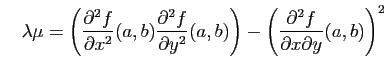
![\begin{displaymath}
\left(
\begin{array}{c}
u_* [2ex]
v_*
\end{array}\right)
=...
...\end{array}\right)
\;\Longleftrightarrow
(u_*,v_*) = (u,v)P\;.
\end{displaymath}](img186.gif)
![\begin{displaymath}
g''(0) = (u_*,v_*)
\left(
\begin{array}{cc}
\lambda&0 [2ex...
..._* [2ex]
v_*
\end{array}\right)
= \lambda u_*^2+\mu v_*^2\;.
\end{displaymath}](img187.gif)
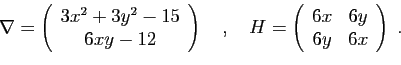
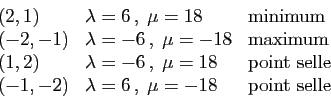
![]() dans
dans
![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales