Nous passons maintenant à un problème un peu différent : la
recherche d'extrema liés, aussi appelés extrema sous
contrainte. Commençons par un exemple simple. Parmi les
parallélépipèdes de surface 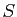 fixée, lesquels ont un volume
maximal ? Si
fixée, lesquels ont un volume
maximal ? Si 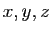 désignent les longueurs des côtés du
parallélépipède, la surface est
désignent les longueurs des côtés du
parallélépipède, la surface est
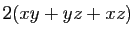 et le volume
et le volume
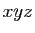 . Le problème est de trouver le maximum atteint par le volume
. Le problème est de trouver le maximum atteint par le volume
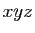 , non pas parmi tous les points de
, non pas parmi tous les points de
 , mais seulement
parmi ceux vérifiant la contrainte
, mais seulement
parmi ceux vérifiant la contrainte
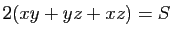 , où
, où 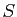 est
fixé. Bien sûr, on peut utiliser la contrainte pour calculer une
des variables en fonction des deux autres. Par exemple pour
est
fixé. Bien sûr, on peut utiliser la contrainte pour calculer une
des variables en fonction des deux autres. Par exemple pour 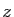 :
:
En reportant cette valeur de 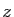 dans l'expression du volume, on
obtient :
dans l'expression du volume, on
obtient :
On peut calculer le maximum de cette fonction avec la technique du
gradient. Le lecteur vérifiera que le maximum de 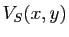 est
atteint pour :
est
atteint pour :
ce qui entraîne aussi
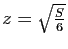 : à surface fixée,
le parallélépipède de volume maximal est le cube.
: à surface fixée,
le parallélépipède de volume maximal est le cube.
Il est rare que l'on puisse effectivement appliquer cette technique de
substitution, surtout s'il y a plusieurs
contraintes. On utilise alors le théorème des multiplicateurs
de Lagrange, qui dit que si un problème d'optimisation sous
contrainte a une solution en un point, alors les gradients de la
fonction et des contraintes sont des vecteurs linéairement
dépendants.
Dans ce théorème,  est la fonction dont on cherche un maximum
ou un minimum, et
est la fonction dont on cherche un maximum
ou un minimum, et
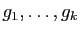 sont les contraintes. Remarquons
qu'il y a au plus
sont les contraintes. Remarquons
qu'il y a au plus 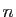 contraintes, car leurs gradients doivent
être linéairement
indépendants. En fait pour que le
théorème ait un intérêt, il ne peut pas y avoir plus de
contraintes, car leurs gradients doivent
être linéairement
indépendants. En fait pour que le
théorème ait un intérêt, il ne peut pas y avoir plus de
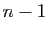 contraintes. Les
coefficients
contraintes. Les
coefficients
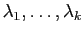 sont les
multiplicateurs de Lagrange. Appliquons ce théorème
au problème du volume sous contrainte de
surface.
sont les
multiplicateurs de Lagrange. Appliquons ce théorème
au problème du volume sous contrainte de
surface.
Si un point 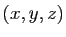 est solution, alors il existe un multiplicateur
est solution, alors il existe un multiplicateur
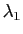 tel que
tel que
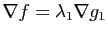 . On doit donc
avoir :
. On doit donc
avoir :
En soustrayant ces équations deux à deux, on obtient :
qui implique que 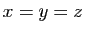 . On retrouve donc la solution
précédente.
. On retrouve donc la solution
précédente.
Voici maintenant un exemple similaire, mais avec deux contraintes.
La contrainte
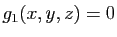 est l'équation de la sphère de centre
est l'équation de la sphère de centre
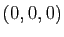 et de rayon
et de rayon 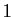 ; la contrainte
; la contrainte
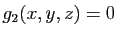 est l'équation d'un
plan. On cherche donc les extrema de
est l'équation d'un
plan. On cherche donc les extrema de  sur l'intersection de la
sphère unité et d'un plan, à savoir sur un cercle dans l'espace.
Si un point
sur l'intersection de la
sphère unité et d'un plan, à savoir sur un cercle dans l'espace.
Si un point 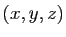 est solution, alors il existe deux multiplicateurs
est solution, alors il existe deux multiplicateurs
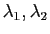 tels que
tels que
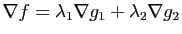 . On doit donc avoir :
. On doit donc avoir :
On obtient donc un système de 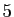 équations (les
équations (les 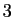 précédentes et les
précédentes et les 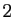 contraintes), et
contraintes), et 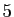 inconnues :
inconnues :
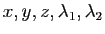 . L'étude de ce système montre
qu'il a
. L'étude de ce système montre
qu'il a 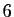 solutions, données dans le tableau ci-dessous.
solutions, données dans le tableau ci-dessous.
Observons que ces points ont été obtenus par une condition
nécessaire. Rien dans le théorème 7 ne
permet de savoir si ce sont des maxima, des minima ou ni l'un ni l'autre.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
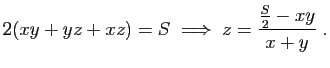
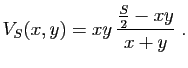
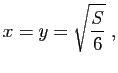
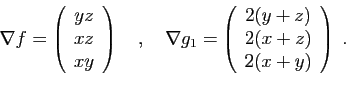
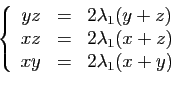
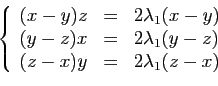
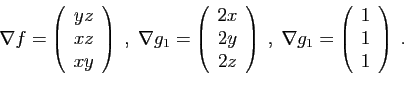
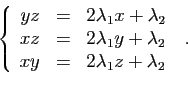
![\begin{displaymath}
\begin{array}{\vert rrrrr\vert}
\hline
x&y&z&\lambda_1&\lamb...
...\frac{1}{3}&-\frac{1}{3}&\frac{2}{9} [1ex]
\hline
\end{array}\end{displaymath}](img245.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales