Nous étudions dans ce chapitre des techniques de calcul pour
des fonctions définies sur un domaine 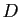 de
de
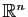 , donc dépendant de
, donc dépendant de 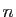 variables réelles, et à valeurs dans
variables réelles, et à valeurs dans
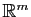 . Nous nous limiterons
souvent aux dimensions
. Nous nous limiterons
souvent aux dimensions 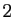 et
et 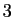 , la généralisation aux
dimensions supérieures ne posant pas de problème
particulier. Voici quelques exemples simples.
Surface d'un rectangle en fonction de sa longueur et sa largeur :
, la généralisation aux
dimensions supérieures ne posant pas de problème
particulier. Voici quelques exemples simples.
Surface d'un rectangle en fonction de sa longueur et sa largeur :
Surface d'un parallélépipède en fonction de ses trois dimensions :
Surface et volume
d'un parallélépipède en fonction de ses trois dimensions :
Coordonnées polaires d'un point du plan (figure
1) :
Figure 1:
Coordonnées polaires d'un point du plan.
|
|
Coordonnées cylindriques d'un point de l'espace (figure
2) :
Figure 2:
Coordonnées cylindriques d'un point de l'espace.
|
|
Coordonnées sphériques d'un point de l'espace (figure
3) :
Figure 3:
Coordonnées sphériques d'un point de l'espace.
|
|
Représenter graphiquement une fonction de plusieurs variables n'est
possible que pour les fonctions de
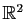 dans
dans
 . La fonction
. La fonction
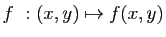 est représentée en dimension
est représentée en dimension 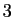 par la surface d'équation
par la surface d'équation 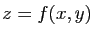 . La figure 4
montre une représentation de la surface d'équation
. La figure 4
montre une représentation de la surface d'équation
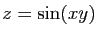 .
.
Figure:
Surface d'équation
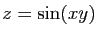 .
.
|
|
Pour ne pas compliquer les notations dans les définitions qui
viennent, nous prendrons l'exemple
d'une application de
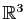 dans
dans
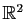 :
:
Les applications  et
et 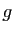 , de
, de
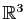 dans
dans
 , sont les
applications coordonnées. Si on fixe un point
, sont les
applications coordonnées. Si on fixe un point 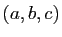 dans
l'espace de départ, on définit 3 applications partielles
pour chaque application coordonnée.
dans
l'espace de départ, on définit 3 applications partielles
pour chaque application coordonnée.
Avant de pouvoir parler de continuité et de dérivabilité, nous
devons définir la notion de limite dans l'espace
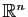 .
.
Définition 1
On dit qu'une suite de points converge dans
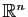 vers un point
vers un point
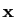 si pour tout
si pour tout 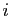 ,
la suite des
,
la suite des 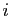 -ièmes coordonnées converge dans
-ièmes coordonnées converge dans
 vers la
vers la
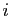 -ième coordonnée de
-ième coordonnée de
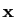 .
.
Dans
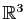 , la suite
, la suite
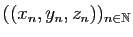 converge
si et seulement si les trois suites
converge
si et seulement si les trois suites
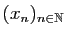 ,
,
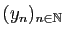 ,
,
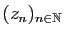 convergent
dans
convergent
dans
 . Par exemple, la suite
. Par exemple, la suite
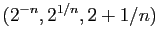 converge
dans
converge
dans
 vers
vers 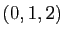 .
.
Définition 2
On dit qu'une application 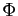 de
de
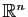 dans
dans
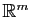 est
continue en un point
est
continue en un point
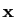 de
de
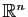 si
l'image par
si
l'image par 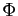 de toute suite de points de
de toute suite de points de
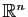 qui converge
vers
qui converge
vers
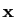 , converge vers
, converge vers
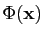 dans
dans
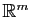 .
.
Comme cas particulier, l'application qui à
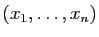 associe la coordonnée
associe la coordonnée 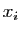 est continue.
D'après la définition de la convergence,
l'application
est continue.
D'après la définition de la convergence,
l'application 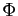 est continue
si et seulement si ses applications coordonnées le sont.
Il suffit donc d'examiner la continuité des applications de
est continue
si et seulement si ses applications coordonnées le sont.
Il suffit donc d'examiner la continuité des applications de
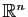 dans
dans
 .
.
Si 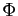 est continue, alors ses applications partielles le
sont aussi. Malheureusement, il peut se faire que les applications
partielles soient continues sans que l'application
est continue, alors ses applications partielles le
sont aussi. Malheureusement, il peut se faire que les applications
partielles soient continues sans que l'application 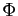 le
soit. Nous n'aborderons pas ce cas pathologique. Toutes les
applications que nous rencontrerons seront continues sur leur domaine
de définition. Pour le vérifier, il suffira en général
d'invoquer le théorème suivant.
le
soit. Nous n'aborderons pas ce cas pathologique. Toutes les
applications que nous rencontrerons seront continues sur leur domaine
de définition. Pour le vérifier, il suffira en général
d'invoquer le théorème suivant.
Théorème 1
- La somme et le produit de deux applications continues
de
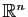 dans
dans
 sont continues.
sont continues.
- La composée d'une application continue de
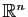 dans
dans
 par une
application continue de
par une
application continue de
 dans
dans
 est continue.
est continue.
Comme premier exemple, considérons 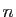 applications continues de
applications continues de
 dans
dans
 ,
,
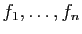 . Pour tout
. Pour tout
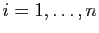 , l'application
, l'application
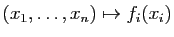 est continue de
est continue de
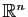 dans
dans
 , comme composée de
, comme composée de 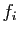 et de la
et de la 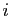 -ième application
coordonnée.
-ième application
coordonnée.
Leur somme
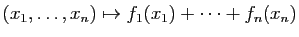 et leur produit
et leur produit
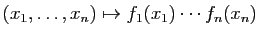 sont aussi continues.
sont aussi continues.
Vérifions maintenant que l'application suivante est continue en
tout point de
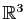
Il suffit de montrer que les deux applications coordonnées sont
continues. L'application qui à 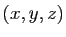 associe
associe 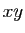 est continue
comme produit de deux applications coordonnées (point 1).
Sa composée par
est continue
comme produit de deux applications coordonnées (point 1).
Sa composée par 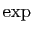 l'est d'après
le point 2. L'application qui à
l'est d'après
le point 2. L'application qui à 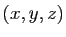 associe
associe
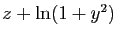 est continue d'après le point 1 et la composée par
est continue d'après le point 1 et la composée par 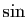 l'est d'après 2. L'application qui à
l'est d'après 2. L'application qui à 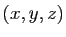 associe
associe
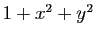 est continue d'après 1, l'inverse d'après
2 (car le dénominateur ne s'annule pas). Finalement le produit de
trois applications continues est continu d'après 1. On
procède de même pour l'autre application coordonnée.
est continue d'après 1, l'inverse d'après
2 (car le dénominateur ne s'annule pas). Finalement le produit de
trois applications continues est continu d'après 1. On
procède de même pour l'autre application coordonnée.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
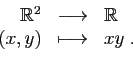
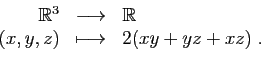
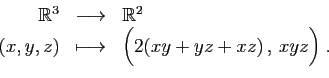
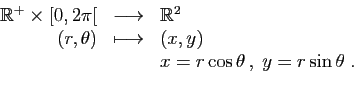
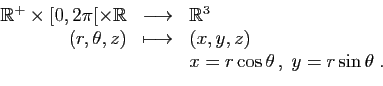
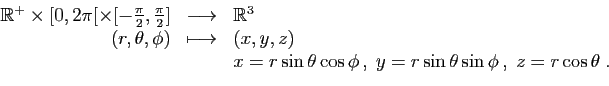
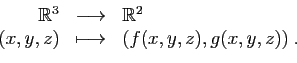
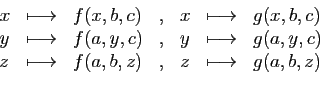
![]() est continue, alors ses applications partielles le
sont aussi. Malheureusement, il peut se faire que les applications
partielles soient continues sans que l'application
est continue, alors ses applications partielles le
sont aussi. Malheureusement, il peut se faire que les applications
partielles soient continues sans que l'application ![]() le
soit. Nous n'aborderons pas ce cas pathologique. Toutes les
applications que nous rencontrerons seront continues sur leur domaine
de définition. Pour le vérifier, il suffira en général
d'invoquer le théorème suivant.
le
soit. Nous n'aborderons pas ce cas pathologique. Toutes les
applications que nous rencontrerons seront continues sur leur domaine
de définition. Pour le vérifier, il suffira en général
d'invoquer le théorème suivant.
![]()
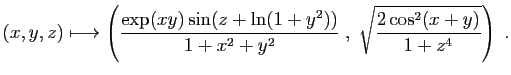
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales