Dans cette section, nous ajoutons une fonction de la variable à
l'équation du second ordre à coefficients constants
de la section précédente.
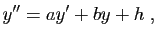 |
(8) |
où 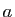 et
et 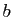 sont deux réels, et
sont deux réels, et 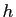 est une fonction de
est une fonction de
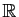 dans
dans
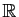 : le second membre.
Comme pour les équations linéaires du premier ordre,
la solution générale de (8) s'obtient en ajoutant
une solution particulière à l'équation sans second membre
(6). Le théorème suivant est l'analogue du
théorème 2.
: le second membre.
Comme pour les équations linéaires du premier ordre,
la solution générale de (8) s'obtient en ajoutant
une solution particulière à l'équation sans second membre
(6). Le théorème suivant est l'analogue du
théorème 2.
Démonstration : Une fonction 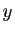 est
solution de (8), si et seulement si
la différence
est
solution de (8), si et seulement si
la différence
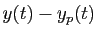 est
solution de l'équation homogène (6). Il suffit alors
d'appliquer le théorème 3.
est
solution de l'équation homogène (6). Il suffit alors
d'appliquer le théorème 3.  L'ensemble des solutions est donc un espace affine de dimension
L'ensemble des solutions est donc un espace affine de dimension 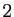 (plan affine). Pour résoudre (8), il suffit de trouver
une solution particulière. Il existe une méthode générale
du type «variation des constantes», mais elle est assez compliquée
à mettre en
(plan affine). Pour résoudre (8), il suffit de trouver
une solution particulière. Il existe une méthode générale
du type «variation des constantes», mais elle est assez compliquée
à mettre en 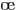 uvre et nous ne la développerons pas ici. Nous
étudierons seulement certains seconds membres particuliers, du type
«exponentielle-polynôme».
La première observation est que les solutions dépendent
linéairement du second membre au sens du résultat suivant, que
l'on appelle aussi principe de superposition des solutions.
uvre et nous ne la développerons pas ici. Nous
étudierons seulement certains seconds membres particuliers, du type
«exponentielle-polynôme».
La première observation est que les solutions dépendent
linéairement du second membre au sens du résultat suivant, que
l'on appelle aussi principe de superposition des solutions.
Démonstration : Il suffit d'écrire les deux équations :
On multiplie la première équation par 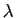 , la seconde par
, la seconde par
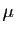 et on ajoute.
et on ajoute. En utilisant ce principe, il est possible de calculer des solutions
particulières, quand
En utilisant ce principe, il est possible de calculer des solutions
particulières, quand 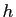 est une combinaison d'exponentielles et de
polynômes, grâce au résultat suivant.
est une combinaison d'exponentielles et de
polynômes, grâce au résultat suivant.
Démonstration : Posons
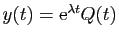 , et calculons :
, et calculons :
En identifiant avec l'équation 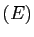 , on voit que
, on voit que 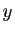 est solution si et
seulement si :
est solution si et
seulement si :
Au second membre apparaît le polynôme inconnu 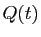 et ses deux
dérivées.
et ses deux
dérivées.
- Si
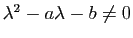 (donc
(donc 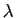 n'est pas
solution de
n'est pas
solution de 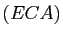 ) : on peut chercher un
polynôme de même degré que
) : on peut chercher un
polynôme de même degré que 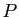 . En identifiant les coefficients,
on aura à résoudre un système linéaire dont la matrice est
carrée et triangulaire : ce système a une solution unique.
. En identifiant les coefficients,
on aura à résoudre un système linéaire dont la matrice est
carrée et triangulaire : ce système a une solution unique.
- Si
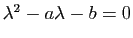 et
et
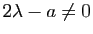 (donc
(donc 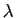 est
racine simple de
est
racine simple de 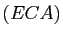 ) : pour équilibrer
les degrés, il faudra choisir
) : pour équilibrer
les degrés, il faudra choisir 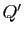 de même degré que
de même degré que
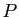 . L'identification des coefficients mène à un système dont
l'ensemble des solutions est une droite affine de dimension
. L'identification des coefficients mène à un système dont
l'ensemble des solutions est une droite affine de dimension 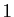 .
.
- Si
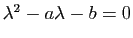 et
et
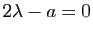 (donc
(donc 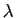 est
racine double de
est
racine double de 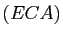 ) : alors
) : alors
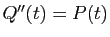 . Par deux
intégrations successives, on
trouve l'ensemble de toutes les solutions de l'équation de
départ : c'est un plan affine.
. Par deux
intégrations successives, on
trouve l'ensemble de toutes les solutions de l'équation de
départ : c'est un plan affine.
 Quand
Quand 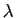 est un réel, l'utilisation de ce théorème ne
pose pas de problème particulier. Voici quelques exemples.
est un réel, l'utilisation de ce théorème ne
pose pas de problème particulier. Voici quelques exemples.
L'utilisation du théorème pour 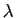 complexe est un
peu plus délicate. Elle permet de traiter le cas où le second
membre est une combinaison linéaire de sinus et cosinus. Examinons
l'exemple suivant.
complexe est un
peu plus délicate. Elle permet de traiter le cas où le second
membre est une combinaison linéaire de sinus et cosinus. Examinons
l'exemple suivant.
Le second membre ne ressemble pas à ceux que nous avons déjà
traités. Mais en linéarisant :
Le principe de superposition des solutions permet de traiter
séparément les équations pour chacun des seconds membres.
Considérons d'abord
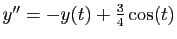 .
Comme
.
Comme
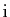 et
et
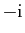 sont racines de
l'équation caractéristique, il faut chercher des solutions sous la
forme
sont racines de
l'équation caractéristique, il faut chercher des solutions sous la
forme
A priori, 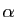 et
et 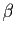 sont des complexes, mais comme nous
cherchons des solutions réelles, celles-ci seront nécessairement de
la forme :
sont des complexes, mais comme nous
cherchons des solutions réelles, celles-ci seront nécessairement de
la forme :
Le calcul direct par indentificaton des coefficients donne
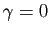 et
et
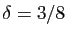 .
.
Traitons mantenant l'équation
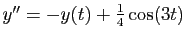 . Puisque
. Puisque
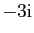 et
et
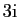 ne sont
pas racines de l'équation caractéristique, on doit chercher des
solutions sous la forme :
ne sont
pas racines de l'équation caractéristique, on doit chercher des
solutions sous la forme :
Comme elles doivent être réelles, on cherchera par identification
des coefficients deux réels 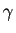 et
et 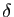 tels que :
tels que :
soit solution. On trouve
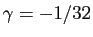 et
et 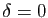 . Voici la
solution générale de l'équation de départ
. Voici la
solution générale de l'équation de départ
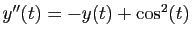 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![\begin{displaymath}
\begin{array}{\vert c\vert c\vert c\vert c\vert}
\hline&&&\\...
...i}&
\mathrm{e}^{t}(\alpha t+\beta) [1.5ex]
\hline
\end{array}\end{displaymath}](img271.gif)
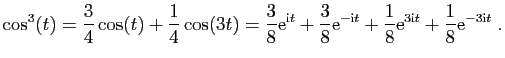
![]() .
Comme
.
Comme
![]() et
et
![]() sont racines de
l'équation caractéristique, il faut chercher des solutions sous la
forme
sont racines de
l'équation caractéristique, il faut chercher des solutions sous la
forme
![]() . Puisque
. Puisque
![]() et
et
![]() ne sont
pas racines de l'équation caractéristique, on doit chercher des
solutions sous la forme :
ne sont
pas racines de l'équation caractéristique, on doit chercher des
solutions sous la forme :
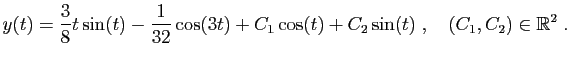
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales