De nombreuses méthodes ont été inventées pour ramener
certaines équations aux cas étudiés dans les sections
précédentes. L'idée générale consiste à modifier soit la
fonction inconnue soit la variable. Nous nous contenterons dans cette
section de donner un exemple pour chacun des deux cas.
Le premier exemple est celui des équations de Bernoulli, qui se
traitent par un changement de fonction.
avec 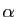 différent de 0 et
différent de 0 et 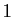 . Observons tout d'abord que
pour
. Observons tout d'abord que
pour 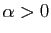 , la
fonction nulle est solution de cette équation. Pour trouver les
autres solutions,
on remplace la fonction inconnue
, la
fonction nulle est solution de cette équation. Pour trouver les
autres solutions,
on remplace la fonction inconnue 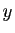 par
par
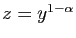 . En
dérivant, on obtient :
. En
dérivant, on obtient :
soit
qui est une équation linéaire. Par exemple :
Le changement de fonction
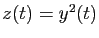 conduit à :
conduit à :
La solution générale de cette équation linéaire est
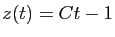 , sur
, sur
![$ ]-\infty,0[ $](img302.gif) , ou bien
, ou bien
![$ ]0,+\infty[ $](img303.gif) .
On en déduit les
solutions de l'équation de Bernoulli initiale, sous la forme
.
On en déduit les
solutions de l'équation de Bernoulli initiale, sous la forme
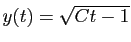 , définie seulement si
, définie seulement si
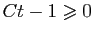 .
.
Nous donnons maintenant un exemple de changement de variable, avec les
équations d'Euler.
où 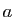 et
et 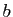 sont deux constantes,
sont deux constantes, 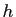 une fonction de
une fonction de
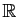 dans
dans
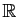 .
Pour
.
Pour
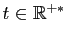 , on pose
, on pose
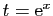 , et
, et
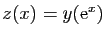 . On a alors :
. On a alors :
En dérivant une fois de plus,
Pour
 , le changement de variable
, le changement de variable
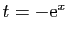 conduit aux
mêmes expressions de
conduit aux
mêmes expressions de 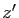 et
et 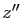 en fonction de
en fonction de 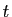 et
et 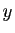 .
On se ramène ainsi, pour
.
On se ramène ainsi, pour
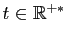 ,
à l'équation linéaire du second ordre en
,
à l'équation linéaire du second ordre en 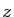 :
:
Par exemple, l'équation
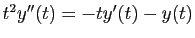 , se ramène à
, se ramène à
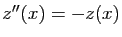 , dont la solution générale est
, dont la solution générale est
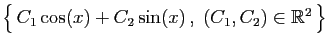 .
La solution générale sur
.
La solution générale sur
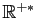 (respectivement :
(respectivement :
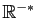 )
s'obtient en remplaçant
)
s'obtient en remplaçant 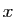 par
par 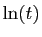 (respectivement :
(respectivement : 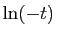 ).
).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
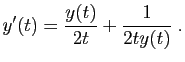
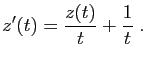
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales