Cette section est consacrée à la résolution d'équations du
type suivant :
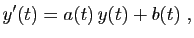 |
(5) |
où 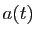 et
et 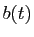 sont deux fonctions données, définies et
continues sur un intervalle
sont deux fonctions données, définies et
continues sur un intervalle 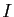 de
de
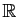 ,
et la fonction inconnue
,
et la fonction inconnue 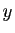 doit être définie et
dérivable sur un intervalle ouvert
doit être définie et
dérivable sur un intervalle ouvert 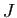 , inclus dans
, inclus dans 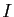 .
La fonction
.
La fonction 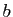 est le second membre.
est le second membre.
On retiendra que la solution générale de l'équation
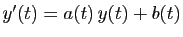 est la somme d'une solution particulière et de la
solution générale de l'équation sans second membre
est la somme d'une solution particulière et de la
solution générale de l'équation sans second membre
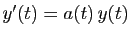 .
L'ensemble des solutions de (5) est une
droite affine, passant par
.
L'ensemble des solutions de (5) est une
droite affine, passant par 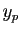 , dont la droite vectorielle
associée est l'ensemble des solutions de l'équation sans second
membre.
Démonstration : Une fonction
, dont la droite vectorielle
associée est l'ensemble des solutions de l'équation sans second
membre.
Démonstration : Une fonction 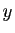 est
solution de (5), si et seulement si
la différence
est
solution de (5), si et seulement si
la différence
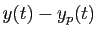 est
solution de l'équation sans second membre (3). Il suffit alors
d'appliquer le théorème 1.
est
solution de l'équation sans second membre (3). Il suffit alors
d'appliquer le théorème 1.  Le théorème 2 suppose la connaissance d'une solution
particulière
Le théorème 2 suppose la connaissance d'une solution
particulière 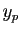 . Ne rêvons pas : les solutions «évidentes» ne
le sont jamais. Vous pouvez toujours essayer de trouver une solution
constante :
. Ne rêvons pas : les solutions «évidentes» ne
le sont jamais. Vous pouvez toujours essayer de trouver une solution
constante :
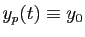 . Il y en a parfois ;
mais s'il n'y en pas, vous perdriez votre
temps à essayer de deviner une solution particulière en cherchant
au hasard. Mieux vaut utiliser la méthode dite de variation de
la constante.
Elle consiste à rechercher les
solutions de (5) sous la forme suivante.
. Il y en a parfois ;
mais s'il n'y en pas, vous perdriez votre
temps à essayer de deviner une solution particulière en cherchant
au hasard. Mieux vaut utiliser la méthode dite de variation de
la constante.
Elle consiste à rechercher les
solutions de (5) sous la forme suivante.
On remplace donc la constante 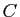 dans la solution générale de
l'équation sans second membre (3),
par une fonction de
dans la solution générale de
l'équation sans second membre (3),
par une fonction de 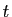 . C'est
pour cela que l'on parle de variation de la
constante. À partir de cette expression de
. C'est
pour cela que l'on parle de variation de la
constante. À partir de cette expression de 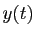 , on calcule
, on calcule
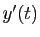 , puis
, puis
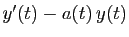 , qui doit être égal à
, qui doit être égal à 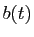 .
.
On en déduit alors 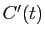 , puis une primitive
, puis une primitive 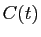 , que
l'on reporte dans l'expression de
, que
l'on reporte dans l'expression de 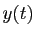 . On obtient l'expression
suivante, qu'il est conseillé de ne pas retenir.
. On obtient l'expression
suivante, qu'il est conseillé de ne pas retenir.
Voici un exemple.
Commençons par résoudre l'équation sans second membre.
La solution générale de l'équation sans second membre est :
où 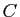 est une constante réelle quelconque.
Cherchons maintenant une solution de l'équation de départ, en
remplaçant
est une constante réelle quelconque.
Cherchons maintenant une solution de l'équation de départ, en
remplaçant 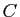 par une fonction
par une fonction 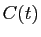 dans la solution
générale de l'équation sans second membre.
dans la solution
générale de l'équation sans second membre.
La solution générale de l'équation avec second membre est :
Comme dans le cas sans second membre, la donnée d'une condition initiale
détermine une solution unique. Il est inutile d'écrire
l'expression générale de cette solution. On l'obtient en calculant
la constante 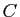 à partir de la solution générale. Voici par
exemple le calcul pour la solution de l'équation précédente
vérifiant
à partir de la solution générale. Voici par
exemple le calcul pour la solution de l'équation précédente
vérifiant 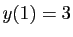 .
.
d'où on tire
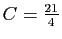 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() de (5) est l'ensemble des
fonctions
de (5) est l'ensemble des
fonctions ![]() de
de ![]() dans
dans
![]() , telles que :
, telles que :
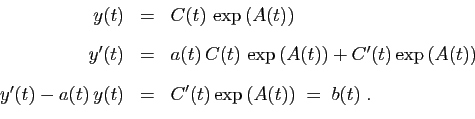
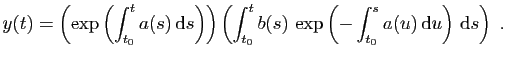
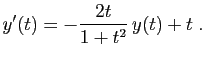
![\begin{displaymath}
\begin{array}{lcl}
y'(t)&=&\displaystyle{-\frac{2t}{1+t^2} ...
... [2ex]
y(t) &=& \displaystyle{
\frac{C}{1+t^2}\;.
}
\end{array}\end{displaymath}](img170.gif)
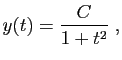
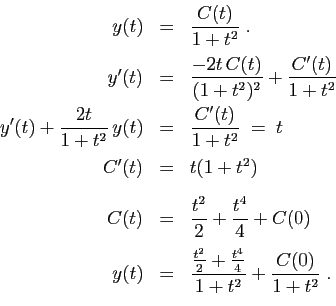
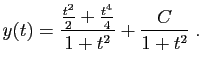
![]() à partir de la solution générale. Voici par
exemple le calcul pour la solution de l'équation précédente
vérifiant
à partir de la solution générale. Voici par
exemple le calcul pour la solution de l'équation précédente
vérifiant ![]() .
.
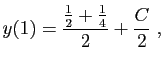
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales