Cette section est consacrée aux équations du type suivant.
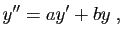 |
(6) |
où 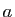 et
et 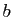 sont deux réels donnés.
Avant d'énoncer le résultat qui donne la solution générale de
(6), commençons par chercher une solution sous la
forme
sont deux réels donnés.
Avant d'énoncer le résultat qui donne la solution générale de
(6), commençons par chercher une solution sous la
forme
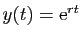 .
.
Si on reporte
ces expressions dans (6), on peut simplifier par
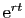 qui est toujours non nul. On obtient
l'équation suivante en
qui est toujours non nul. On obtient
l'équation suivante en 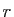 .
.
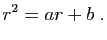 |
(7) |
Cette équation porte le nom d'équation caractéristique associée
(ECA). C'est
la condition nécessaire et suffisante
pour que
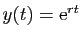 soit solution de
(6). La solution générale de (6)
s'exprime à l'aide des racines de l'ECA.
soit solution de
(6). La solution générale de (6)
s'exprime à l'aide des racines de l'ECA.
Théorème 3
Soit 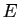 l'ensemble des solutions de
l'ensemble des solutions de (
6)
,
définies sur
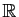 . L'ensemble
. L'ensemble 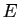 est un sous-espace
vectoriel de dimension
est un sous-espace
vectoriel de dimension 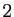 de
de
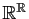 .
Si l'équation caractéristique associée possède
.
Si l'équation caractéristique associée possède
- deux racines réelles distinctes
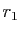 et
et 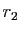 , alors :
, alors :
- une racine double
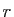 , alors :
, alors :
- deux racines complexes conjuguées
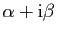 et
et
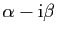 , alors :
, alors :
Voici des exemples illustrant les trois cas (vérifiez les
calculs).
Démonstration : Nous donnons ici une démonstration élémentaire, sans aucun outil
d'algèbre linéaire.
Nous commençons par le cas où l'équation
caractéristique associée a son discriminant positif ou nul,
c'est-à-dire soit deux solutions réelles distinctes, soit une solution
double. Nous avons déjà vérifié que
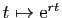 est
solution de (6) si et seulement si
est
solution de (6) si et seulement si 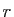 est solution de
l'équation caractéristique associée. Dans le cas où
est solution de
l'équation caractéristique associée. Dans le cas où 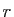 est
racine double, vous vérifierez que
est
racine double, vous vérifierez que
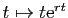 est aussi solution de (6). Or si
est aussi solution de (6). Or si  et
et  sont deux solutions de (6), alors pour tous
sont deux solutions de (6), alors pour tous
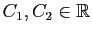 , la fonction
, la fonction
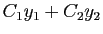 est encore solution (donc
est encore solution (donc
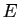 est un sous-espace vectoriel de
est un sous-espace vectoriel de
 ). Ceci montre que dans les
2 premiers cas, toutes les fonctions proposées sont bien des
solutions de l'équation différentielle. Nous devons prouver que ce
sont les seules.
). Ceci montre que dans les
2 premiers cas, toutes les fonctions proposées sont bien des
solutions de l'équation différentielle. Nous devons prouver que ce
sont les seules.
Soit 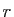 une racine de l'équation caractéristique associée. Soit
une racine de l'équation caractéristique associée. Soit
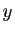 une fonction telle que
une fonction telle que
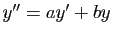 . Considérons la fonction
. Considérons la fonction 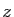 définie pour tout
définie pour tout
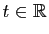 par :
par :
Écrivons en fonction de 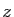 les dérivées successives de
les dérivées successives de 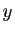 .
.
Multiplions 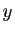 par
par 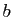 ,
, 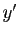 par
par 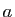 ,
, 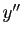 par
par 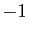 et
ajoutons. Comme
et
ajoutons. Comme 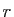 vérifie
vérifie 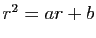 , les termes en
, les termes en 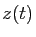 disparaissent, et après simplification par
disparaissent, et après simplification par
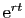 il reste :
il reste :
Donc 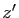 vérifie une équation linéaire du premier ordre. Le
théorème 1 donne la solution générale :
vérifie une équation linéaire du premier ordre. Le
théorème 1 donne la solution générale :
Observons que dans l'équation caractéristique associée, la somme
des deux racines est égale à 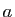 . Il peut se faire que
. Il peut se faire que 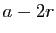 soit
nul : c'est le cas si
soit
nul : c'est le cas si 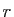 est racine double. Dans ce cas :
est racine double. Dans ce cas :
C'est le point 2 du théorème.
Supposons maintenant
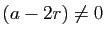 : l'équation
caractéristique associée a deux racines réelles distinctes,
qui sont
: l'équation
caractéristique associée a deux racines réelles distinctes,
qui sont 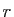 et
et 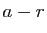 .
.
En posant
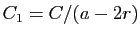 , ceci démontre le point 1 du
théorème.
, ceci démontre le point 1 du
théorème.
Le cas où l'équation caractéristique associée a deux racines
complexes est un peu plus délicat si vous n'avez pas l'habitude de
dériver des fonctions à valeurs complexes. Nous nous contenterons
d'esquisser l'argument. Il se trouve que tout ce que nous venons de
dire pour des racines réelles, reste vrai pour des racines
complexes. La même démonstration prouve que l'ensemble des
fonctions à valeurs complexes vérifiant 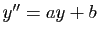 est :
est :
Reste à extraire de cet ensemble les fonctions à valeurs
réelles. Pour qu'une des fonctions écrites ci-dessus ne prenne que
des valeurs réelles pour
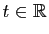 , il est nécessaire et suffisant
que les deux constantes
, il est nécessaire et suffisant
que les deux constantes
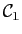 et
et
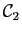 soient deux
complexes conjugués. L'ensemble des fonctions à valeurs réelles
solution de l'équation (6) peut donc s'écrire :
soient deux
complexes conjugués. L'ensemble des fonctions à valeurs réelles
solution de l'équation (6) peut donc s'écrire :
Or :
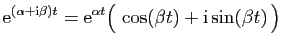
et
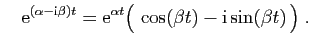
On en déduit :
D'où le résultat, en remplaçant 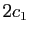 par
par 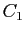 et
et 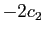 par
par 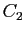 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![\begin{displaymath}
\begin{array}{\vert c\vert c\vert c\vert c\vert}
\hline&&&\\...
...os(3t)+C_2\mathrm{e}^{-2t}\sin(3t) [1.5ex]
\hline
\end{array}\end{displaymath}](img192.gif)
![]() une racine de l'équation caractéristique associée. Soit
une racine de l'équation caractéristique associée. Soit
![]() une fonction telle que
une fonction telle que
![]() . Considérons la fonction
. Considérons la fonction ![]() définie pour tout
définie pour tout
![]() par :
par :
![]() : l'équation
caractéristique associée a deux racines réelles distinctes,
qui sont
: l'équation
caractéristique associée a deux racines réelles distinctes,
qui sont ![]() et
et ![]() .
.
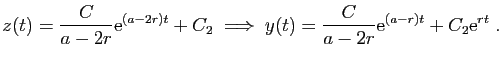
![]() est :
est :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales