Cette section est consacrée à la résolution d'équations du
type suivant :
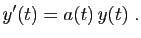 |
(3) |
Dans cet énoncé 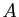 est une primitive quelconque de
est une primitive quelconque de
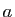 . Deux primitives diffèrent par une constante
additive. Remplacer une primitive par une autre dans
(4) ajoute une constante dans
l'exponentielle, donc multiplie l'exponentielle par une constante.
L'ensemble des solutions de (3) est une
droite vectorielle : toutes les solutions sont proportionnelles entre elles.
. Deux primitives diffèrent par une constante
additive. Remplacer une primitive par une autre dans
(4) ajoute une constante dans
l'exponentielle, donc multiplie l'exponentielle par une constante.
L'ensemble des solutions de (3) est une
droite vectorielle : toutes les solutions sont proportionnelles entre elles.
Dans le cas particulier où 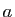 est
constante, la solution générale de l'équation
est
constante, la solution générale de l'équation
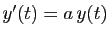 est
est
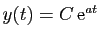 , ce que vous saviez déjà.
Démonstration : Multiplions les deux membres de (3) par
, ce que vous saviez déjà.
Démonstration : Multiplions les deux membres de (3) par
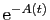 , qui
est toujours non nul. Toute solution de (3) vérifie aussi :
, qui
est toujours non nul. Toute solution de (3) vérifie aussi :
Or le premier membre est la dérivée de
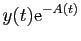 .
Donc
.
Donc 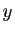 est solution si et seulement si
la fonction
est solution si et seulement si
la fonction
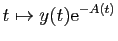 a une
dérivée nulle sur
a une
dérivée nulle sur 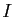 , c'est-à-dire
s'il existe une constante
, c'est-à-dire
s'il existe une constante 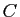 telle que pour
tout
telle que pour
tout 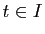 ,
,
Ainsi, pour tout 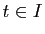 ,
,
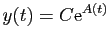 .
.  Il n'est pas conseillé de retenir (4)
par c
Il n'est pas conseillé de retenir (4)
par c ur, mais plutôt de refaire le calcul pour chaque équation
par le moyen mnémotechnique suivant (non rigoureux mais efficace).
Commençons par mettre
(3) sous la forme
ur, mais plutôt de refaire le calcul pour chaque équation
par le moyen mnémotechnique suivant (non rigoureux mais efficace).
Commençons par mettre
(3) sous la forme
sans nous préoccuper de la nullité éventuelle de 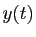 .
Si on prend une primitive de chaque membre, les deux primitives
doivent être égales à une constante près, que l'on note
.
Si on prend une primitive de chaque membre, les deux primitives
doivent être égales à une constante près, que l'on note
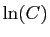 .
.
L'exponentielle des deux membres donne :
Si la valeur absolue de 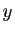 est proportionnelle à
est proportionnelle à
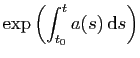 , soit
, soit 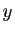 est
nulle partout, soit
est
nulle partout, soit 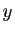 ne s'annule nulle part. Dans ce dernier cas,
comme les fonctions
ne s'annule nulle part. Dans ce dernier cas,
comme les fonctions 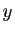 et
et 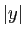 sont continues,
sont continues,
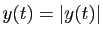 partout
ou bien
partout
ou bien
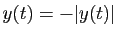 partout. On retrouve donc
(4).
partout. On retrouve donc
(4).
Voici un exemple.
Observons que dans ce cas la fonction 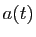 n'est pas définie en
0. On ne pourra donc résoudre l'équation que sur
l'un des deux intervalles
n'est pas définie en
0. On ne pourra donc résoudre l'équation que sur
l'un des deux intervalles
![$ ]-\infty,0 [$](img123.gif) ou
ou
![$ ] 0,+\infty[ $](img124.gif) . La méthode ci-dessus se détaille comme suit.
. La méthode ci-dessus se détaille comme suit.
Malgré l'expression obtenue,
les solutions ne peuvent pas être définies sur
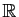 tout entier, puisque l'équation
n'a pas de sens en
tout entier, puisque l'équation
n'a pas de sens en 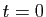 . La fonction définie par
. La fonction définie par
est solution de l'équation, sur
![$ ]-\infty,0 [$](img123.gif) et sur
et sur
![$ ] 0,+\infty[ $](img124.gif) .
.
Outre déterminer la solution générale, on peut aussi
chercher une solution vérifiant une condition donnée ; c'est le problème
de Cauchy.
Démonstration : La vérification, en utilisant le théorème 1, est
immédiate.
La technique de résolution des équations linéaires homogènes
reste valable pour des équations différentielles du type
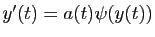 , pourvu que l'on sache calculer une primitive
de
, pourvu que l'on sache calculer une primitive
de
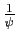 . Voici un exemple.
. Voici un exemple.
avec
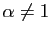 . En divisant par
. En divisant par 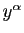 puis en
prenant la primitive des deux membres, on obtient :
puis en
prenant la primitive des deux membres, on obtient :
Si
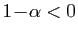 ,
, 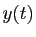 tend vers
tend vers 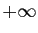 quand
quand 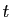 tend vers
tend vers 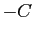 par valeurs inférieures, et
par valeurs inférieures, et 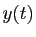 n'est pas défini
pour
n'est pas défini
pour 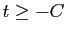 .
On dit que la solution «explose en temps fini»,
dans le cas présent, au
temps
.
On dit que la solution «explose en temps fini»,
dans le cas présent, au
temps 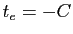 . Remarquons que pour une solution initiale
. Remarquons que pour une solution initiale 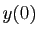 strictement positive donnée, le temps d'explosion vaut
strictement positive donnée, le temps d'explosion vaut
Donc 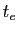 est une fonction décroissante
de
est une fonction décroissante
de 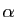 . Intuitivement, cela traduit le fait que plus le taux
d'accroissement est fort, plus l'explosion a lieu rapidement.
À titre d'exemple, la figure 5 représente
quelques solutions de l'équation
. Intuitivement, cela traduit le fait que plus le taux
d'accroissement est fort, plus l'explosion a lieu rapidement.
À titre d'exemple, la figure 5 représente
quelques solutions de l'équation
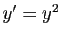 .
.
Figure 5:
Explosion en temps fini : solutions de 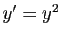 , partant de
, partant de
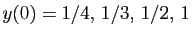 .
.
|
|
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() est
constante, la solution générale de l'équation
est
constante, la solution générale de l'équation
![]() est
est
![]() , ce que vous saviez déjà.
Démonstration : Multiplions les deux membres de (3) par
, ce que vous saviez déjà.
Démonstration : Multiplions les deux membres de (3) par
![]() , qui
est toujours non nul. Toute solution de (3) vérifie aussi :
, qui
est toujours non nul. Toute solution de (3) vérifie aussi :
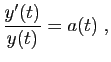
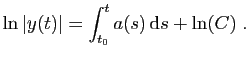
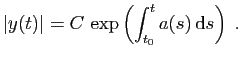
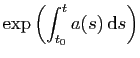 , soit
, soit 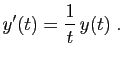
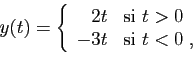
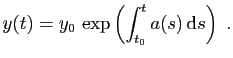
![]() , pourvu que l'on sache calculer une primitive
de
, pourvu que l'on sache calculer une primitive
de
![]() . Voici un exemple.
. Voici un exemple.
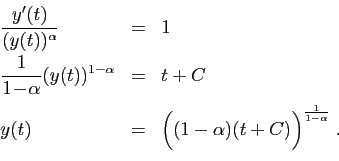
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales