Nous reprenons les notations de la section précédente :  et
et  sont deux espaces vectoriels, munis respectivement des bases
sont deux espaces vectoriels, munis respectivement des bases
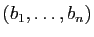 et
et
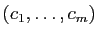 . La matrice de l'application
linéaire
. La matrice de l'application
linéaire  relative à ces deux bases est
relative à ces deux bases est 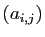 . Le noyau
de
. Le noyau
de  est l'ensemble des vecteurs de
est l'ensemble des vecteurs de  dont l'image par
dont l'image par  est le
vecteur nul. Soit
est le
vecteur nul. Soit  un vecteur de
un vecteur de  et
et
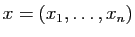 le
le
 -uplet de ses coordonnées dans la base
-uplet de ses coordonnées dans la base
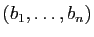 .
La condition nécessaire et suffisante sur
.
La condition nécessaire et suffisante sur 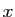 pour que
pour que 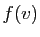 soit nul
est que toutes les coordonnées de
soit nul
est que toutes les coordonnées de 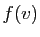 , c'est-à-dire
toutes les lignes du produit
, c'est-à-dire
toutes les lignes du produit 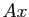 , soient nulles.
, soient nulles.
Le système linéaire  est homogène : l'ensemble de ses
solutions est un sous-espace vectoriel de
est homogène : l'ensemble de ses
solutions est un sous-espace vectoriel de
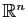 . La méthode du
pivot de Gauss permet de déterminer une base de l'ensemble des
solutions de
. La méthode du
pivot de Gauss permet de déterminer une base de l'ensemble des
solutions de  , donc une base de
, donc une base de
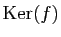 . Nous allons voir
qu'elle permet aussi au passage de déterminer le rang de
. Nous allons voir
qu'elle permet aussi au passage de déterminer le rang de  ,
et même une base de
,
et même une base de
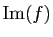 .
.
D'après la proposition 8, à toute famille de  vecteurs de
vecteurs de
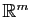 correspond une application linéaire de
correspond une application linéaire de
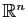 dans
dans
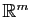 . Nous avons vu que le rang de cette application
est le rang de la famille de vecteurs
(définitions 10 et
14). La
technique décrite ici s'applique indifféremment à une famille
de vecteurs ou à une application linéaire.
La première étape de la méthode de Gauss consiste à mettre le
système
. Nous avons vu que le rang de cette application
est le rang de la famille de vecteurs
(définitions 10 et
14). La
technique décrite ici s'applique indifféremment à une famille
de vecteurs ou à une application linéaire.
La première étape de la méthode de Gauss consiste à mettre le
système  sous forme échelonnée.
sous forme échelonnée.
Mettre le système  sous forme échelonnée, c'est
passer de
sous forme échelonnée, c'est
passer de  à
à 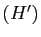 par des transformations de lignes
consistant à ajouter à une ligne le produit d'une autre par une
constante, échanger deux lignes,
permuter éventuellement des
coordonnées, de sorte que
par des transformations de lignes
consistant à ajouter à une ligne le produit d'une autre par une
constante, échanger deux lignes,
permuter éventuellement des
coordonnées, de sorte que
- les systèmes
 et
et 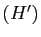 sont équivalents,
sont équivalents,
- les inconnues
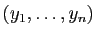 de
de 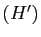 sont celles de
sont celles de  ,
mais dans un ordre qui peut être différent,
,
mais dans un ordre qui peut être différent,
- les pivots
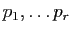 sont tous non nuls.
sont tous non nuls.
Au système 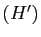 on peut associer la matrice suivante.
on peut associer la matrice suivante.
Cette matrice est celle d'une autre application linéaire 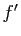 , de
, de
 vers
vers  .
.
Théorème 13
Les applications  et
et 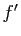 sont de rang
sont de rang 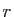 .
.
-
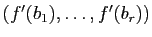 est une base de
est une base de
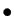
- Soient
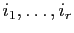 les indices tels que
les indices tels que
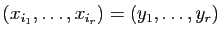 .
.
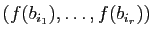 est une base de
est une base de
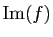 .
.
Démonstration : La famille
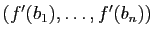 engendre
engendre
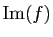 , car
, car
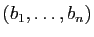 engendre
engendre  . Or tous ces vecteurs appartiennent
au sous-espace de
. Or tous ces vecteurs appartiennent
au sous-espace de  , engendré par
, engendré par
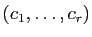 . Donc
. Donc
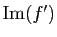 est de dimension au plus
est de dimension au plus 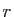 . Pour montrer que
le rang de
. Pour montrer que
le rang de 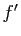 est
est 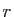 et que
et que
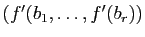 est une
base de
est une
base de
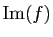 , il suffit de vérifier que c'est une famille
libre. Nous devons montrer
, il suffit de vérifier que c'est une famille
libre. Nous devons montrer
Utilisant les coordonnées dans la base
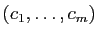 , les
, les
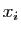 doivent vérifier le système :
doivent vérifier le système :
Nous devons montrer que ce système a pour unique solution
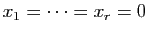 . C'est une récurrence facile sur
. C'est une récurrence facile sur
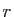 . Si
. Si  , le système se réduit à l'équation
, le système se réduit à l'équation
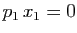 , qui a pour seule solution
, qui a pour seule solution 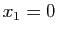 , car le
pivot
, car le
pivot 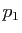 est non nul. Supposons le résultat vrai pour tout
système du même type, de taille
est non nul. Supposons le résultat vrai pour tout
système du même type, de taille 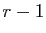 , et considérons
la dernière équation du
système de taille
, et considérons
la dernière équation du
système de taille 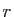 . Si elle est satisfaite, alors
. Si elle est satisfaite, alors 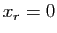 ,
car le pivot
,
car le pivot 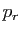 est non nul. En reportant
est non nul. En reportant 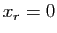 dans les
équations précédentes, on obtient un système du même type,
mais de taille
dans les
équations précédentes, on obtient un système du même type,
mais de taille 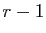 : la seule solution est
: la seule solution est
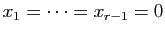 , par
l'hypothèse de récurrence.
Les deux systèmes
, par
l'hypothèse de récurrence.
Les deux systèmes  et
et 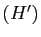 ayant le même ensemble de
solutions, les applications
ayant le même ensemble de
solutions, les applications  et
et 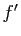 ont le même noyau, et donc
le même rang, d'après le théorème du rang 12. La
dimension de
ont le même noyau, et donc
le même rang, d'après le théorème du rang 12. La
dimension de
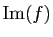 est donc
est donc 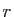 . Pour montrer qu'un ensemble
de
. Pour montrer qu'un ensemble
de 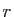 vecteurs est une base, il suffit de vérifier que c'est une
famille libre. Inutile d'écrire le système en
vecteurs est une base, il suffit de vérifier que c'est une
famille libre. Inutile d'écrire le système en
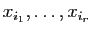 qui exprime que
qui exprime que
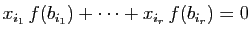 : il se déduit de
: il se déduit de  en annulant les variables autres que
en annulant les variables autres que
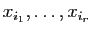 . La
chaîne de tranformations qui conduit de
. La
chaîne de tranformations qui conduit de  à
à 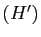 conduit
forcément de ce nouveau système,
au système
conduit
forcément de ce nouveau système,
au système 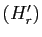 ci-dessus. Les deux systèmes ont le même
ensemble de solutions, d'où le résultat.
ci-dessus. Les deux systèmes ont le même
ensemble de solutions, d'où le résultat.
La technique est beaucoup plus facile à appliquer qu'il n'y paraît.
Considérons l'application suivante, de
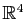 dans
dans
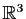 :
:
Sa matrice, relative aux bases canoniques de
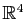 au départ, et
au départ, et
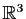 à l'arrivée est :
à l'arrivée est :
Le système homogène permettant de déterminer
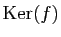 est :
est :
Le système est de rang 2, il en est de même de l'application
 . La mise sous forme échelonnée montre que les colonnes de
. La mise sous forme échelonnée montre que les colonnes de 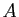 correspondant aux variables
correspondant aux variables 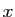 et
et 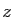 , à savoir la première et la
troisième, forment une famille libre, donc une base de
, à savoir la première et la
troisième, forment une famille libre, donc une base de
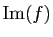 .
.
Nous avons écrit les vecteurs en colonnes, pour souligner le fait
qu'il s'agit nécessairement de vecteurs colonnes de la matrice 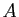 .
Pour trouver une base de
.
Pour trouver une base de
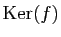 , il faut continuer la
résolution.
, il faut continuer la
résolution.
L'ensemble des solutions est l'ensemble des quadruplets
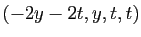 , où
, où 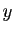 et
et 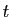 sont deux réels quelconques.
Donc :
sont deux réels quelconques.
Donc :
C'est un sous-espace de dimension 2 dans
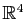 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
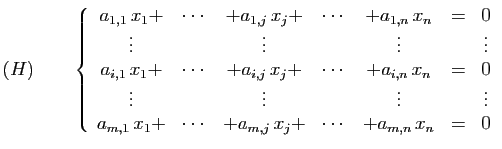
![]() vecteurs de
vecteurs de
![]() correspond une application linéaire de
correspond une application linéaire de
![]() dans
dans
![]() . Nous avons vu que le rang de cette application
est le rang de la famille de vecteurs
(définitions 10 et
14). La
technique décrite ici s'applique indifféremment à une famille
de vecteurs ou à une application linéaire.
La première étape de la méthode de Gauss consiste à mettre le
système
. Nous avons vu que le rang de cette application
est le rang de la famille de vecteurs
(définitions 10 et
14). La
technique décrite ici s'applique indifféremment à une famille
de vecteurs ou à une application linéaire.
La première étape de la méthode de Gauss consiste à mettre le
système ![]() sous forme échelonnée.
sous forme échelonnée.
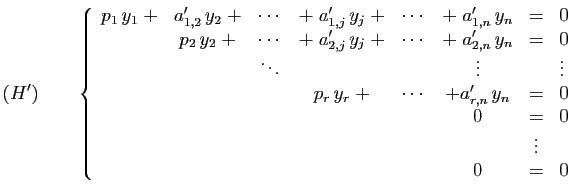
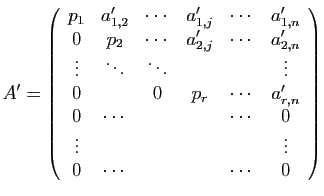
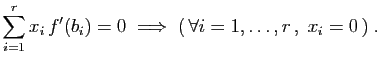
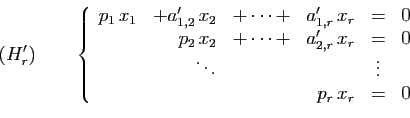
![]() dans
dans
![]() :
:
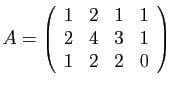
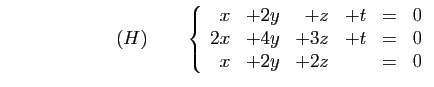
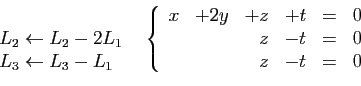
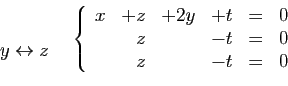
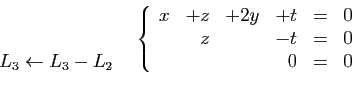
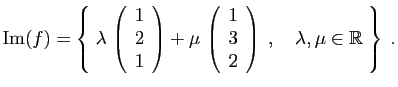
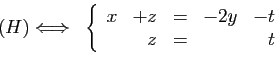
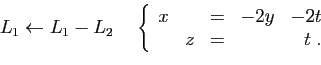
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales