En un point où la dérivée d'une fonction s'annule, les
accroissements de la fonction sont négligeables devant les
accroissements de la variable. Souvent, c'est un point
où les variations de la fonction changent de sens, donc un maximum
ou un minimum.
Insistons sur l'adjectif local. Il suffit que la valeur de  en
en  soit la plus grande des valeurs prises par
soit la plus grande des valeurs prises par  sur un petit
intervalle autour de
sur un petit
intervalle autour de  pour que
pour que  soit un maximum local.
Cette valeur n'est pas nécessairement la plus grande prise par
soit un maximum local.
Cette valeur n'est pas nécessairement la plus grande prise par  sur tout son domaine de définition (voir le graphe de la figure
3).
sur tout son domaine de définition (voir le graphe de la figure
3).
Théorème 4
Soit  une fonction de
une fonction de
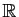 dans
dans
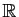 , définie sur un intervalle
ouvert
, définie sur un intervalle
ouvert  . Si
. Si  présente un extremum (maximum ou minimum)
local en un point
présente un extremum (maximum ou minimum)
local en un point  de
de  ,
et si
,
et si  est dérivable en
est dérivable en  , alors
, alors 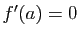 .
.
Démonstration : Si  est un minimum local de
est un minimum local de  , alors c'est un
maximum local de
, alors c'est un
maximum local de 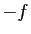 : quitte à remplacer
: quitte à remplacer  par
par 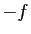 , nous pouvons
supposer que
, nous pouvons
supposer que  est un maximum local.
est un maximum local.
Donc pour tout 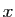 dans l'intervalle
dans l'intervalle
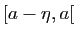 ,
,
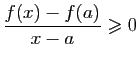
donc
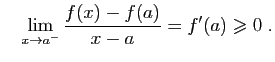
Pour tout 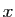 dans l'intervalle
dans l'intervalle
![$ ]a,a+\eta[ $](img180.gif) ,
,
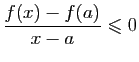
donc
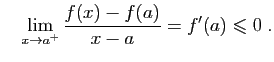
D'où le résultat. Reprenons l'exemple de la figure 2 :
Reprenons l'exemple de la figure 2 :
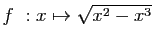 . La dérivée est :
. La dérivée est :
Elle s'annule en 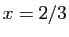 , et
, et  admet effectivement un maximum en ce
point. Mais savoir que
admet effectivement un maximum en ce
point. Mais savoir que 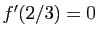 permet seulement d'affirmer que la
tangente en ce point est horizontale.
Il se pourrait que la dérivée en un point soit nulle sans
que la fonction admette un extremum en ce point : par exemple la
fonction
permet seulement d'affirmer que la
tangente en ce point est horizontale.
Il se pourrait que la dérivée en un point soit nulle sans
que la fonction admette un extremum en ce point : par exemple la
fonction
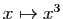 en 0.
D'autre part,
une fonction peut présenter un extremum en
en 0.
D'autre part,
une fonction peut présenter un extremum en  , sans être
dérivable en ce point (par exemple la fonction
, sans être
dérivable en ce point (par exemple la fonction
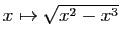 en 0).
en 0).
Voici un autre exemple
(figure 3). Soit  la fonction définie par :
la fonction définie par :
Figure:
Graphe de la fonction
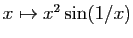 .
.
|
|
Le taux d'accroissement de  en 0 est
en 0 est
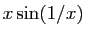 , qui tend vers
0. La dérivée de
, qui tend vers
0. La dérivée de  en 0 est donc nulle. Pourtant, tout
intervalle contenant 0, contient aussi des valeurs positives, et des
valeurs négatives (et aussi une infinité d'extrema locaux).
Nous allons appliquer le théorème 4, pour
démontrer le théorème de Rolle.
en 0 est donc nulle. Pourtant, tout
intervalle contenant 0, contient aussi des valeurs positives, et des
valeurs négatives (et aussi une infinité d'extrema locaux).
Nous allons appliquer le théorème 4, pour
démontrer le théorème de Rolle.
Démonstration : Une application continue sur intervalle fermé borné, atteint sa
borne inférieure 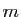 et sa borne supérieure
et sa borne supérieure 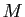 : il existe
: il existe
![$ c_1,
c_2\in[a,b]$](img198.gif) tels que pour tout
tels que pour tout
![$ x\in [a,b]$](img199.gif) ,
,
Si 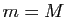 , l'application
, l'application  est constante sur
est constante sur ![$ [a,b]$](img193.gif) , et sa
dérivée est identiquement nulle. Si
, et sa
dérivée est identiquement nulle. Si 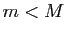 , alors l'une au moins
de ces deux valeurs est différente de
, alors l'une au moins
de ces deux valeurs est différente de 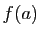 (et donc de
(et donc de
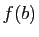 ). Si
). Si 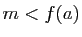 , alors
, alors
![$ c_1\in ]a,b[$](img205.gif) est un minimum pour
est un minimum pour  , et
donc
, et
donc 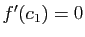 , d'après le théorème précédent. Si
, d'après le théorème précédent. Si
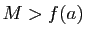 , alors
, alors 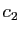 est un maximum pour
est un maximum pour  , et donc
, et donc 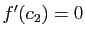 .
.
Figure 4:
Théorème de Rolle.
|
|
Figure 5:
Théorème des accroissements finis.
|
|
On en déduit le résultat le plus
important de cette section,
le théorème des accroissements finis.
Démonstration : Considérons la fonction  , qui à
, qui à ![$ x\in [a,b]$](img199.gif) associe
associe
La fonction  est continue sur
est continue sur ![$ [a,b]$](img193.gif) , dérivable sur
, dérivable sur ![$ ]a,b[ $](img194.gif) . De
plus, elle prend la même valeur en
. De
plus, elle prend la même valeur en  et
et 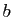 :
:
D'après le théorème de Rolle, la dérivée de 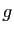 s'annule en
un point
s'annule en
un point 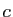 de
de ![$ ]a,b[ $](img194.gif) .
.
D'où le résultat. Graphiquement, le théorème des accroissements finis dit que la
courbe représentative de
Graphiquement, le théorème des accroissements finis dit que la
courbe représentative de  sur
sur ![$ [a,b]$](img193.gif) possède au moins une
tangente parallèle à la sécante passant par
possède au moins une
tangente parallèle à la sécante passant par 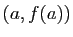 et
et 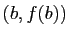 (figure 5). Si
(figure 5). Si 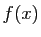 représente la position d'un
mobile à l'instant
représente la position d'un
mobile à l'instant 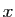 , le théorème des accroissements finis dit
que en au moins un point, la vitesse instantanée doit être
égale à la vitesse moyenne sur l'intervalle.
, le théorème des accroissements finis dit
que en au moins un point, la vitesse instantanée doit être
égale à la vitesse moyenne sur l'intervalle.
Le plus souvent en pratique, on ne sait rien de la valeur de 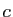 qui
est telle que la tangente en
qui
est telle que la tangente en 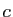 est parallèle à la
sécante. Mais de son existence découlent des inégalités
permettant d'obtenir des renseignements précis sur les
accroissements de la fonction.
Le théorème des accroissements finis permet aussi d'établir le
lien entre le sens de variation de
est parallèle à la
sécante. Mais de son existence découlent des inégalités
permettant d'obtenir des renseignements précis sur les
accroissements de la fonction.
Le théorème des accroissements finis permet aussi d'établir le
lien entre le sens de variation de  et le signe de sa dérivée.
et le signe de sa dérivée.
Proposition 6
Soit  un intervalle ouvert non vide, et
un intervalle ouvert non vide, et  une fonction
dérivable sur
une fonction
dérivable sur  . La fonction
. La fonction  est :
est :
- croissante sur
 si et seulement si
si et seulement si 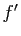 est positive ou
nulle sur
est positive ou
nulle sur  ,
,
- décroissante sur
 si et seulement si
si et seulement si 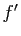 est négative ou
nulle sur
est négative ou
nulle sur  .
.
Démonstration : La fonction  est croissante si et seulement si
est croissante si et seulement si 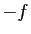 est
décroissante. Il suffit donc de démontrer le premier point.
Si
est
décroissante. Il suffit donc de démontrer le premier point.
Si  est croissante, alors ses taux d'accroissement sont tous
positifs ou nuls :
est croissante, alors ses taux d'accroissement sont tous
positifs ou nuls :
Comme la dérivée en chaque point est limite de taux
d'accroissement, elle est aussi positive ou nulle.
Réciproquement, soient 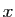 et
et 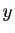 deux points de
deux points de  tels que
tels que
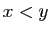 . Appliquons le théorème des accroissements finis à
. Appliquons le théorème des accroissements finis à  sur
l'intervalle
sur
l'intervalle ![$ [x,y]$](img221.gif) : il existe
: il existe
![$ c\in ]x,y[$](img222.gif) tel que :
tel que :
Donc
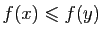 .
. Ce résultat n'est valable que sur un intervalle : la fonction
Ce résultat n'est valable que sur un intervalle : la fonction
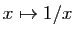 a une dérivée négative sur
a une dérivée négative sur
 , pourtant elle
n'est pas décroissante. D'autre part, si la dérivée est
strictement positive, alors la fonction est strictement croissante. La
réciproque est fausse. La fonction peut être strictement croissante
même si la dérivée s'annule en certains points (par exemple
, pourtant elle
n'est pas décroissante. D'autre part, si la dérivée est
strictement positive, alors la fonction est strictement croissante. La
réciproque est fausse. La fonction peut être strictement croissante
même si la dérivée s'annule en certains points (par exemple
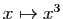 ).
Comme autre application du théorème des accroissements finis,
il est possible d'obtenir la dérivée en un point comme
prolongement par continuité de la dérivée calculée sur un
intervalle.
).
Comme autre application du théorème des accroissements finis,
il est possible d'obtenir la dérivée en un point comme
prolongement par continuité de la dérivée calculée sur un
intervalle.
Démonstration : Soit
![$ x\in ]a,b]$](img228.gif) . Appliquons le théorème des accroissements finis
sur l'intervalle
. Appliquons le théorème des accroissements finis
sur l'intervalle ![$ [a,x]$](img21.gif) . Il existe
. Il existe
![$ c\in ]a,x[$](img229.gif) tel que
tel que
Soit 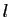 la limite à droite de
la limite à droite de 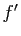 en
en  .
Pour tout
.
Pour tout
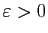 , il existe
, il existe 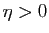 tel que
tel que
Donc pour
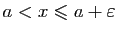 ,
,
D'où le résultat. Ce résultat n'est qu'une condition suffisante. Il peut se faire que la
dérivée existe sans qu'elle soit continue. Par exemple la fonction
Ce résultat n'est qu'une condition suffisante. Il peut se faire que la
dérivée existe sans qu'elle soit continue. Par exemple la fonction
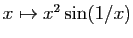 a une dérivée nulle en 0 (figure
3). Pourtant sa dérivée en
a une dérivée nulle en 0 (figure
3). Pourtant sa dérivée en 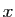 ,
,
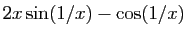 , n'a pas de limite en 0.
, n'a pas de limite en 0.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
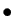
 si
si
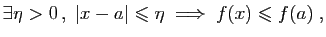
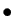
 si
si
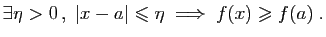
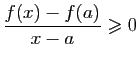 donc
donc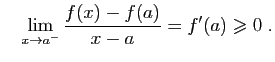
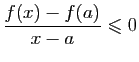 donc
donc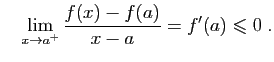
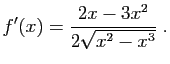
![]() la fonction définie par :
la fonction définie par :
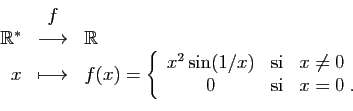
![$\displaystyle \exists c\in ]a,b[\;,\quad \frac{f(b)-f(a)}{b-a}=f'(c)\;.
$](img212.gif)
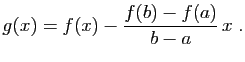
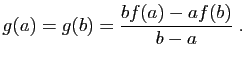
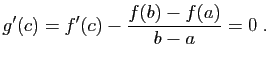
![]() qui
est telle que la tangente en
qui
est telle que la tangente en ![]() est parallèle à la
sécante. Mais de son existence découlent des inégalités
permettant d'obtenir des renseignements précis sur les
accroissements de la fonction.
Le théorème des accroissements finis permet aussi d'établir le
lien entre le sens de variation de
est parallèle à la
sécante. Mais de son existence découlent des inégalités
permettant d'obtenir des renseignements précis sur les
accroissements de la fonction.
Le théorème des accroissements finis permet aussi d'établir le
lien entre le sens de variation de ![]() et le signe de sa dérivée.
et le signe de sa dérivée.
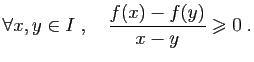
![]() et
et ![]() deux points de
deux points de ![]() tels que
tels que
![]() . Appliquons le théorème des accroissements finis à
. Appliquons le théorème des accroissements finis à ![]() sur
l'intervalle
sur
l'intervalle ![]() : il existe
: il existe
![]() tel que :
tel que :
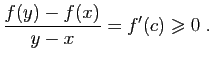
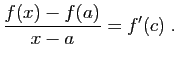
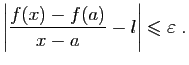
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales