Si 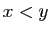 , et
, et
![$ \lambda\in[0,1]$](img239.gif) , alors
, alors
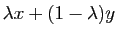 est un point de l'intervalle
est un point de l'intervalle ![$ [x,y]$](img221.gif) . La condition
(2) dit que le point de la courbe représentative
d'abscisse
. La condition
(2) dit que le point de la courbe représentative
d'abscisse
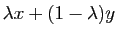 doit
être situé au-dessous du segment de sécante joignant les points
doit
être situé au-dessous du segment de sécante joignant les points
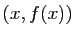 et
et 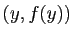 (figure 6). En d'autres
termes, tout arc de la courbe représentative doit être
situé au-dessous de sa corde. De manière
équivalente, la partie du plan située au-dessus
de la courbe représentative est une région convexe,
au sens où tout segment joignant deux de ses points est
entièrement contenu dans la région.
(figure 6). En d'autres
termes, tout arc de la courbe représentative doit être
situé au-dessous de sa corde. De manière
équivalente, la partie du plan située au-dessus
de la courbe représentative est une région convexe,
au sens où tout segment joignant deux de ses points est
entièrement contenu dans la région.
Figure 6:
Courbe représentative d'une fonction convexe.
|
|
Une fonction est dite concave si son opposée est
convexe. Les propriétés sont inversées : tout arc est
au-dessus de sa corde. La région du plan située au-dessous
de la courbe représentative est convexe.
La fonction exponentielle est convexe, la fonction logarithme est
concave. La fonction
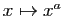 est convexe sur
est convexe sur
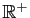 pour
pour
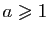 , elle est concave pour
, elle est concave pour
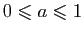 . La fonction
. La fonction
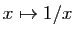 est convexe sur
est convexe sur
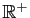 , concave sur
, concave sur
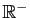 ,
de même que la fonction
,
de même que la fonction
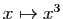 .
Voici une autre caractérisation de la convexité.
.
Voici une autre caractérisation de la convexité.
Démonstration : Commmençons par la condition nécessaire. Soit 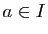 et
et
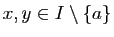 tels que
tels que
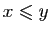 .
Trois cas sont possibles :
.
Trois cas sont possibles :
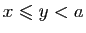 ,
, 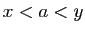 ,
,
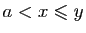 .
Nous traitons le premier, les deux autres sont analogues. Soit
.
Nous traitons le premier, les deux autres sont analogues. Soit
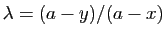 . Alors
. Alors
 . Comme
. Comme  est convexe,
est convexe,
On en déduit :
soit :
Montrons maintenant la condition suffisante. Soient 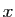 et
et 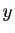 deux
points de
deux
points de  tels que
tels que 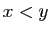 et
et 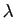 un réel dans
un réel dans ![$ [0,1]$](img261.gif) .
Posons
.
Posons
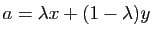 , et donc :
, et donc :
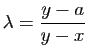
et
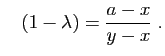
Si 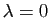 ou
ou 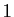 , l'inégalité est
vérifiée. Nous pouvons donc supposer que
, l'inégalité est
vérifiée. Nous pouvons donc supposer que  est différent de
est différent de 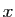 et
et 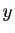 . Écrivons que le taux d'accroissement en
. Écrivons que le taux d'accroissement en  est croissant.
est croissant.
En multipliant les deux membres par le produit
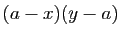 ,
qui est positif, on obtient :
,
qui est positif, on obtient :
En divisant par 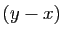 ceci donne :
ceci donne :

Corollaire 1
Si une fonction  est convexe sur un intervalle ouvert
est convexe sur un intervalle ouvert  ,
alors elle est dérivable à gauche et à droite en tout point de
,
alors elle est dérivable à gauche et à droite en tout point de
 , et donc continue sur
, et donc continue sur  .
.
Démonstration : Si 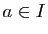 , le taux d'accroissement en
, le taux d'accroissement en  ,
, 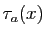 , est une
fonction croissante de
, est une
fonction croissante de 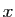 . Il admet donc en
. Il admet donc en  une
limite à gauche et une limite à droite finies.
une
limite à gauche et une limite à droite finies. Ce résultat n'est pas valable si l'intervalle n'est pas ouvert. Par
exemple la fonction qui vaut 0 sur
Ce résultat n'est pas valable si l'intervalle n'est pas ouvert. Par
exemple la fonction qui vaut 0 sur 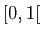 , et
, et 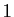 au point
au point 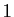 est
convexe sur
est
convexe sur ![$ [0,1]$](img261.gif) , mais elle n'est pas continue en
, mais elle n'est pas continue en 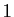 . Le
fait qu'une dérivée à gauche et à droite existe, n'implique pas
que la fonction soit dérivable. Par exemple, la fonction valeur
absolue
. Le
fait qu'une dérivée à gauche et à droite existe, n'implique pas
que la fonction soit dérivable. Par exemple, la fonction valeur
absolue
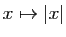 est convexe sur
est convexe sur
 mais elle n'est pas
dérivable en 0. Lorsque la fonction est dérivable, sa
dérivée est croissante.
mais elle n'est pas
dérivable en 0. Lorsque la fonction est dérivable, sa
dérivée est croissante.
Proposition 9
Soit  une fonction de
une fonction de
 dans
dans
 , dérivable
sur un intervalle ouvert
, dérivable
sur un intervalle ouvert  . La fonction
. La fonction  est convexe
sur
est convexe
sur  si et seulement si sa dérivée
si et seulement si sa dérivée 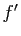 est croissante
sur
est croissante
sur  .
.
Démonstration : Commençons par la condition nécessaire. Soient 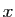 et
et 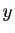 deux
points de
deux
points de  , tels que
, tels que 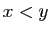 . Pour tout
. Pour tout
![$ z\in [x,y]$](img272.gif) ,
,
En faisant tendre 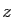 vers
vers 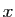 , on en déduit :
, on en déduit :
De même, en faisant tendre 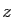 vers
vers 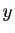 ,
,
Donc
 .
.
Montrons maintenant la condition suffisante.
Soient 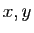 deux points
de
deux points
de  tels que
tels que 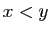 ,
,
![$ \lambda\in ]0,1[ $](img279.gif) , et
, et
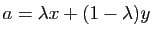 . Appliquons le théorème des accroissements finis
sur les deux intervalles
. Appliquons le théorème des accroissements finis
sur les deux intervalles ![$ [x,a]$](img280.gif) et
et ![$ [a,y]$](img281.gif) . Il existe
. Il existe
![$ c_1\in ]x,a[$](img282.gif) et
et
![$ c_2\in ]a,y[$](img283.gif) tels que :
tels que :
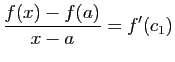
et
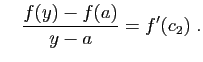
La fonction 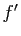 étant croissante, on a donc :
étant croissante, on a donc :
Comme nous l'avons déjà vu dans la démonstration
de la proposition 8, ceci entraîne
 Graphiquement, la pente de la tangente d'une fonction convexe est
croissante. Dans la démonstration précédente, nous avons
établi les inégalités :
Graphiquement, la pente de la tangente d'une fonction convexe est
croissante. Dans la démonstration précédente, nous avons
établi les inégalités :
On en déduit que pour  ,
,
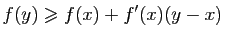
et
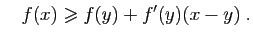
Donc la courbe représentative de  reste au-dessus de ses
tangentes (figure 6).
reste au-dessus de ses
tangentes (figure 6).
Corollaire 2
Soit  une fonction de
une fonction de
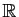 dans
dans
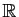 , deux fois
dérivable sur un intervalle ouvert
, deux fois
dérivable sur un intervalle ouvert  . La fonction
. La fonction  est convexe
sur
est convexe
sur  si et seulement si sa dérivée seconde
si et seulement si sa dérivée seconde 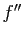 est
positive ou nulle sur
est
positive ou nulle sur  .
.
Une fonction deux fois dérivable est concave si et seulement
si sa dérivée seconde est négative ou nulle.
Les points où la dérivée seconde s'annule et change de signe
correspondent graphiquement à des points où
la courbe représentative passe de concave à convexe où
inversement. On les appelle des points d'inflexion.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() est convexe sur
est convexe sur
![]() pour
pour
![]() , elle est concave pour
, elle est concave pour
![]() . La fonction
. La fonction
![]() est convexe sur
est convexe sur
![]() , concave sur
, concave sur
![]() ,
de même que la fonction
,
de même que la fonction
![]() .
Voici une autre caractérisation de la convexité.
.
Voici une autre caractérisation de la convexité.
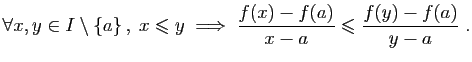
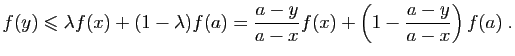
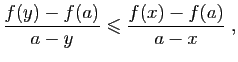
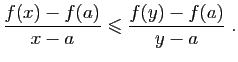
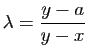 et
et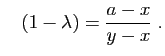
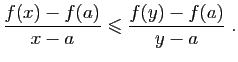
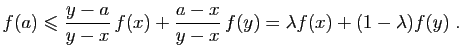
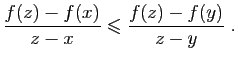
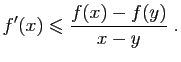
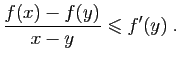
![]() deux points
de
deux points
de ![]() tels que
tels que ![]() ,
,
![]() , et
, et
![]() . Appliquons le théorème des accroissements finis
sur les deux intervalles
. Appliquons le théorème des accroissements finis
sur les deux intervalles ![]() et
et ![]() . Il existe
. Il existe
![]() et
et
![]() tels que :
tels que :
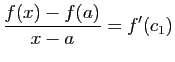 et
et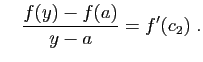
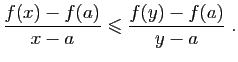

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales