Etant donné un intervalle ouvert  , on dit que
, on dit que  est
dérivable sur
est
dérivable sur  , si elle est dérivable en
tout point de
, si elle est dérivable en
tout point de  . Soit
. Soit  une fonction dérivable sur
une fonction dérivable sur  . Sa
dérivée
. Sa
dérivée 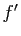 peut être elle-même dérivable. On appelle alors
dérivée seconde la dérivée de
peut être elle-même dérivable. On appelle alors
dérivée seconde la dérivée de 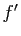 , et on la note
, et on la note
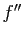 . Cette fonction peut être elle-même dérivable, etc. Si
. Cette fonction peut être elle-même dérivable, etc. Si  est
est 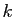 fois dérivable, on note
fois dérivable, on note 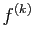 sa dérivée d'ordre
sa dérivée d'ordre
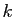 , ou dérivée
, ou dérivée 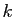 -ième. Par définition, la
dérivée d'ordre 0 est la fonction elle-même.
Par exemple, si
-ième. Par définition, la
dérivée d'ordre 0 est la fonction elle-même.
Par exemple, si 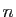 est un entier fixé, et
est un entier fixé, et  est la fonction
est la fonction
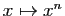 ,
,
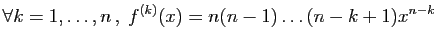
et
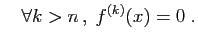
Vous rencontrerez souvent les notations suivantes, que nous
n'utiliserons pas ici.
Définition 5
Soit  une fonction définie sur un intervalle
une fonction définie sur un intervalle  de
de
 . On dit
que
. On dit
que  est de classe
est de classe
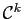 sur
sur  , ou encore
, ou encore
 est
est 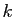 fois continûment dérivable, si elle admet une
dérivée
fois continûment dérivable, si elle admet une
dérivée 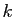 -ième continue sur
-ième continue sur  .
.
On dit que  est de classe
est de classe
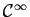 sur
sur  , si elle admet des
dérivées successives de tout ordre (elles sont nécessairement
continues puisque dérivables).
Vous pouvez retenir que :
, si elle admet des
dérivées successives de tout ordre (elles sont nécessairement
continues puisque dérivables).
Vous pouvez retenir que :
toutes les fonctions usuelles sont de classe
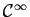
sur les intervalles ouverts où elles sont définies.
Ceci concerne les fonctions polynômes, fractions rationnelles,
puissances, exponentielle, logarithme,
sinus, cosinus.
La formule de Leibniz,
très proche de la formule du binôme de Newton, exprime
la dérivée 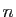 -ième d'un produit à d'aide des dérivées
successives des composantes.
-ième d'un produit à d'aide des dérivées
successives des composantes.
Démonstration : par récurrence sur 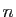 . Puisque par
définition
. Puisque par
définition 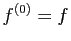 , la formule est vraie pour
, la formule est vraie pour 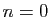 .
Supposons qu'elle est vraie pour
.
Supposons qu'elle est vraie pour 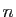 .
Si
.
Si  et
et 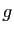 sont dérivables
sont dérivables 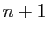 fois sur
fois sur  , alors pour tout
, alors pour tout
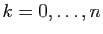 ,
le produit
,
le produit
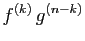 est dérivable et sa dérivée est :
est dérivable et sa dérivée est :
D'après (1), 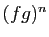 est dérivable, comme combinaison
linéaire de fonctions dérivables. Sa dérivée s'écrit :
est dérivable, comme combinaison
linéaire de fonctions dérivables. Sa dérivée s'écrit :
Pour la dernière égalité, nous avons appliqué la formule du
triangle de Pascal. La formule est vraie pour 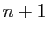 , donc pour tout
, donc pour tout
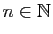 , par récurrence.
, par récurrence. À titre d'exemple, calculons la dérivée
À titre d'exemple, calculons la dérivée 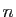 -ième de
-ième de
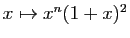 . Posons
. Posons
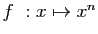 et
et
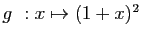 .
Alors :
.
Alors :
et
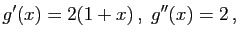
et
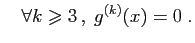
Par application de (1),
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
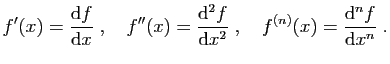
![]() -ième d'un produit à d'aide des dérivées
successives des composantes.
-ième d'un produit à d'aide des dérivées
successives des composantes.
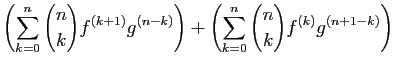
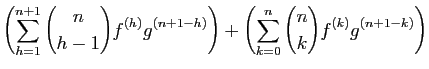
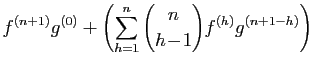
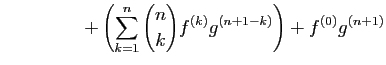
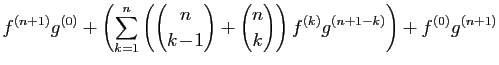
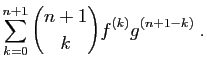
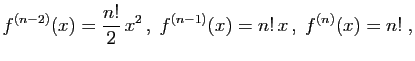
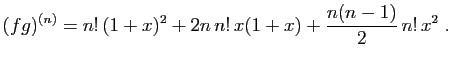
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales