Comme vous le savez, la convergence d'une série est équivalente
par définition à la convergence de la suite des sommes
partielles. Les théorèmes portant sur la
continuité, l'intégration et la dérivation d'une suite de
fonctions s'appliquent aux suites de sommes partielles, donc aux
séries de fonctions. Au-delà de la récriture des résultats de la
section 1.2, l'enjeu principal de cette section sera de fournir des
moyens de vérifier l'hypothèse principale de convergence uniforme,
pour les sommes partielles d'une série.
Les résultats suivants sont des traductions immédiates des
théorèmes
4,
5 et 6.
Théorème 11
Soit  un intervalle de
un intervalle de
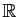 et
et
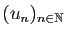 une suite de
fonctions continues sur
une suite de
fonctions continues sur  , à valeurs dans
, à valeurs dans
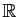 ou
ou
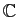 .
Soit
.
Soit 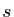 une fonction de
une fonction de  dans
dans
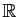 ou
ou
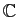 .
Si la série
.
Si la série 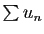 converge uniformément vers
converge uniformément vers 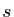 , alors
, alors 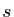 est continue sur
est continue sur  .
.
La convergence uniforme d'une série n'est pas toujours
facile à vérifier. Heureusement on dispose de conditions suffisantes
assez simples.
Définition 6
Soit  un intervalle de
un intervalle de
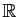 et
et
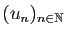 une suite de
fonctions définies sur
une suite de
fonctions définies sur  , à valeurs dans
, à valeurs dans
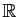 ou
ou
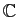 .
On dit que la série
.
On dit que la série 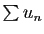 converge normalement sur
converge normalement sur  si la série
si la série
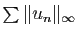 converge.
converge.
Proposition 2
Si une série converge normalement sur un intervalle, alors elle
converge uniformément sur ce même intervalle.
Démonstration : Par définition de la norme uniforme, pour tout 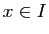 ,
,
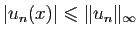 . Par le théorème de comparaison
des séries,
. Par le théorème de comparaison
des séries,
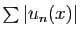 converge, donc
converge, donc
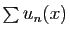 converge
absolument. Soit
converge
absolument. Soit
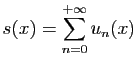 sa somme.
sa somme.
Le dernier majorant est le reste d'une série
convergente, et il ne dépend pas de  : la convergence est bien
uniforme.
: la convergence est bien
uniforme.  Il n'est pas indispensable de calculer
Il n'est pas indispensable de calculer
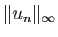 explicitement : il suffit d'en connaître un
majorant, qui soit le terme général d'une série convergente.
explicitement : il suffit d'en connaître un
majorant, qui soit le terme général d'une série convergente.
Corollaire 1
Soit 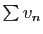 une série convergente telle que
une série convergente telle que
Alors la série 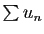 est normalement, donc uniformément convergente.
est normalement, donc uniformément convergente.
L'autre critère utile est la version uniforme du théorème d'Abel.
Démonstration : Les hypothèses assurent que
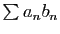 converge simplement, par
le théorème d'Abel pour les séries numériques. Notons
converge simplement, par
le théorème d'Abel pour les séries numériques. Notons 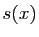 sa somme.
Pour tout
sa somme.
Pour tout
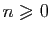 et pour tout
et pour tout 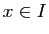 ,
posons
,
posons
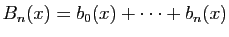 .
Par hypothèse, la suite
.
Par hypothèse, la suite
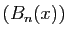 est uniformément bornée.
Écrivons le reste de la
série
est uniformément bornée.
Écrivons le reste de la
série
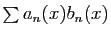 sous la forme suivante.
sous la forme suivante.
La suite 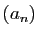 converge uniformément vers 0, il en est donc de
même de la suite
converge uniformément vers 0, il en est donc de
même de la suite 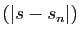 .
. Rappelons que si l'intervalle
Rappelons que si l'intervalle  est fermé borné, alors la
convergence simple vers 0 d'une suite décroissante implique sa convergence
uniforme, par le théorème de Dini 10. La convergence
simple des
est fermé borné, alors la
convergence simple vers 0 d'une suite décroissante implique sa convergence
uniforme, par le théorème de Dini 10. La convergence
simple des 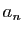 vers 0 est donc suffisante dans l'hypothèse
2. Dans de
nombreux cas, les
vers 0 est donc suffisante dans l'hypothèse
2. Dans de
nombreux cas, les 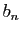 ne dépendent pas de
ne dépendent pas de  , et donc la question
de l'uniformité de la majoration des sommes partielles ne se pose
pas : par exemple pour
les séries alternées où
, et donc la question
de l'uniformité de la majoration des sommes partielles ne se pose
pas : par exemple pour
les séries alternées où
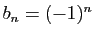 . Considérons le cas
où
. Considérons le cas
où
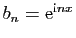 . Les sommes partielles
. Les sommes partielles 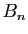 se calculent
explicitement :
se calculent
explicitement :
Elles sont uniformément bornées, sur tout intervalle
fermé borné ne contenant aucun réel de la forme
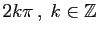 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
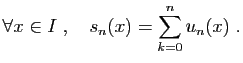
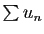 converge simplement vers
converge simplement vers 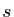 sur
sur
 si la suite
si la suite 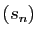 converge simplement vers
converge simplement vers 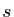 sur
sur  .
.
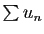 converge uniformément vers
converge uniformément vers 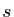 sur
sur
 si la suite
si la suite 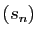 converge uniformément vers
converge uniformément vers 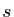 sur
sur  .
.
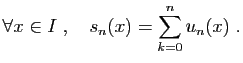
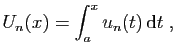
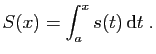
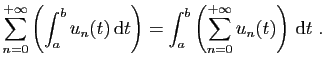
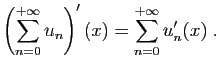
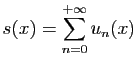 sa somme.
sa somme.
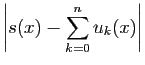
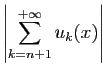
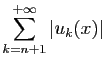
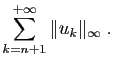
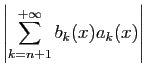
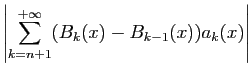
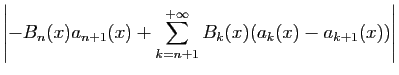
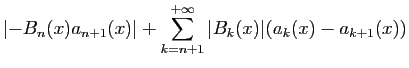
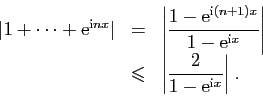
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales