Nous commençons par expliciter à nouveau l'hypothèse de
convergence uniforme dans le cas d'une suite de fonctions.
La convergence uniforme est naturellement associée à la
norme uniforme.
Rappelons que toute partie majorée de
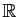 admet une borne
supérieure finie, et que par convention la borne supérieure d'une
partie non majorée est
admet une borne
supérieure finie, et que par convention la borne supérieure d'une
partie non majorée est 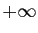 .
Vous apprendrez plus tard que les normes servent à évaluer les
distances dans les espaces vectoriels, et vous saurez pourquoi
celle-ci, parmi toutes les normes possibles dans les espaces vectoriels
de fonctions, est affublée d'un indice
.
Vous apprendrez plus tard que les normes servent à évaluer les
distances dans les espaces vectoriels, et vous saurez pourquoi
celle-ci, parmi toutes les normes possibles dans les espaces vectoriels
de fonctions, est affublée d'un indice 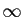 . Pour l'instant, elle
va nous permettre de rendre la convergence uniforme un peu plus
lisible.
. Pour l'instant, elle
va nous permettre de rendre la convergence uniforme un peu plus
lisible.
Démonstration : Reprenons la définition :
Cette définition dit qu'à partir de 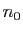 ,
,
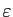 est un majorant
de
est un majorant
de
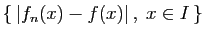 , ce qui entraîne que
, ce qui entraîne que
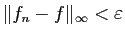 (la borne supérieure est le plus petit des
majorants). Donc
(la borne supérieure est le plus petit des
majorants). Donc
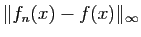 tend vers 0.
tend vers 0.
Réciproquement, si
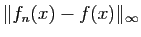 tend vers 0, alors, pour tout
tend vers 0, alors, pour tout
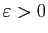 , il existe
, il existe 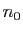 tel que
tel que
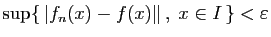 , donc pour tout
, donc pour tout 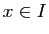 ,
,
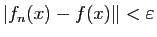 .
.  La figure 1 donne un support géométrique à
votre intuition. Si
La figure 1 donne un support géométrique à
votre intuition. Si 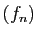 converge uniformément vers
converge uniformément vers  , alors
pour
, alors
pour 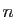 assez grand, le graphe de
assez grand, le graphe de 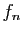 reste dans un «tube»
de largeur constante
reste dans un «tube»
de largeur constante
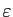 autour du graphe de
autour du graphe de  .
.
Figure 1:
Convergence uniforme d'une suite de fonctions.
|
|
La proposition 1 fournit un moyen de démontrer qu'une
convergence est uniforme : il suffit de trouver un majorant 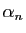 de l'ensemble
de l'ensemble
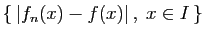 , puis de montrer que
, puis de montrer que
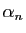 tend vers 0. Réciproquement, pour montrer qu'une
convergence n'est pas uniforme, recherchez
le maximum de
tend vers 0. Réciproquement, pour montrer qu'une
convergence n'est pas uniforme, recherchez
le maximum de
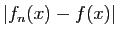 : s'il ne tend pas vers 0, la
convergence n'est pas uniforme. Par exemple
: s'il ne tend pas vers 0, la
convergence n'est pas uniforme. Par exemple
![$ f_n : x\mapsto\mathbb{I}_{]0,\frac{1}{n}]}(x)$](img146.gif) converge simplement vers la
fonction nulle, mais la convergence n'est pas uniforme car le maximum
de
converge simplement vers la
fonction nulle, mais la convergence n'est pas uniforme car le maximum
de 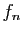 est
est 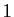 .
Avant d'étudier les conséquences de la convergence uniforme,
insistons à nouveau sur le fait que la limite simple d'une suite de
fonctions continues n'est pas nécessairement une fonction
continue. Nous avons déjà donné l'exemple de
.
Avant d'étudier les conséquences de la convergence uniforme,
insistons à nouveau sur le fait que la limite simple d'une suite de
fonctions continues n'est pas nécessairement une fonction
continue. Nous avons déjà donné l'exemple de
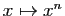 sur
sur
![$ [0,1]$](img149.gif) , en voici un autre. Pour tout
, en voici un autre. Pour tout
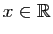 et pour tout
et pour tout
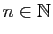 , soit
, soit
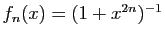 . La suite de fonctions
. La suite de fonctions
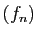 converge simplement.
converge simplement.
Si la convergence d'une suite de fonctions continues
est uniforme, la limite est bien
continue.
Théorème 4
Soit  un intervalle de
un intervalle de
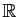 et
et
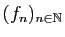 une suite de
fonctions continues sur
une suite de
fonctions continues sur  , à valeurs dans
, à valeurs dans
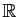 ou
ou
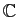 .
Soit
.
Soit  une fonction de
une fonction de  dans
dans
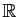 ou
ou
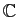 .
Si la suite
.
Si la suite 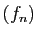 converge uniformément vers
converge uniformément vers  , alors
, alors  est continue sur
est continue sur  .
.
Démonstration : Pour tout 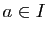 ,
,
car 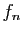 est continue en
est continue en 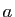 .
Comme la convergence est uniforme, le théorème
2 donne :
.
Comme la convergence est uniforme, le théorème
2 donne :
 Il s'agit bien d'une condition suffisante : une limite non
uniforme de fonctions continues peut très bien être continue : par
exemple
Il s'agit bien d'une condition suffisante : une limite non
uniforme de fonctions continues peut très bien être continue : par
exemple
![$ f_n : x\mapsto\mathbb{I}_{]0,\frac{1}{n}]}(x)$](img146.gif) converge
(simplement) vers la fonction nulle. Il en est d'ailleurs de même de
converge
(simplement) vers la fonction nulle. Il en est d'ailleurs de même de
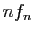 . Or l'intégrale de
. Or l'intégrale de 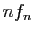 sur
sur ![$ [0,1]$](img149.gif) vaut
vaut 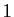 :
l'intégrale de la limite simple d'une suite de fonctions
n'est pas forcément l'intégrale de la limite. Là encore, la
convergence uniforme est la bonne hypothèse.
:
l'intégrale de la limite simple d'une suite de fonctions
n'est pas forcément l'intégrale de la limite. Là encore, la
convergence uniforme est la bonne hypothèse.
Démonstration : La fonction  est limite uniforme d'une suite de fonctions continues,
elle est donc continue (théorème 4). En tant
que fonction continue, elle est
intégrable sur
est limite uniforme d'une suite de fonctions continues,
elle est donc continue (théorème 4). En tant
que fonction continue, elle est
intégrable sur ![$ [a,b]$](img159.gif) , et sa primitive
, et sa primitive 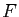 est donc bien
définie. De plus pour tout
est donc bien
définie. De plus pour tout
![$ x\in [a,b]$](img164.gif) :
:
Or par hypothèse,
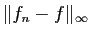 tend vers 0 :
tend vers 0 :
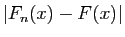 est majoré indépendamment de
est majoré indépendamment de  par un terme qui
tend vers 0. Donc la suite
par un terme qui
tend vers 0. Donc la suite 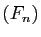 converge vers
converge vers 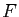 uniformément sur
uniformément sur ![$ [a,b]$](img159.gif) .
.  La convergence uniforme sur
La convergence uniforme sur  permet d'intégrer, mais pas de
dériver, comme le montre l'exemple suivant.
permet d'intégrer, mais pas de
dériver, comme le montre l'exemple suivant.
La suite 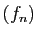 converge uniformément sur
converge uniformément sur
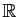 vers
vers
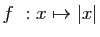 . En effet, pour tout
. En effet, pour tout
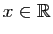 :
:
Pourtant 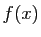 n'est pas dérivable en 0, bien que la suite des
dérivées
n'est pas dérivable en 0, bien que la suite des
dérivées 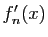 converge (simplement).
converge (simplement).
Par contre, si la suite des dérivées converge uniformément, on
peut intégrer, et ce qui est vrai pour les primitives doit l'être pour
les dérivées, si on fait attention à bien ajuster la constante
d'intégration.
Démonstration : Comme 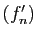 est une suite de fonctions continues qui converge
uniformément, sa limite
est une suite de fonctions continues qui converge
uniformément, sa limite 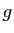 est une fonction continue (théorème
4). Pour tout
est une fonction continue (théorème
4). Pour tout
![$ x\in ]a,b[$](img186.gif) , posons
, posons
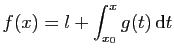
où
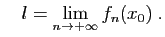
Par le théorème fondamental de l'analyse,  est continûment
dérivable sur
est continûment
dérivable sur ![$ ]a,b[$](img179.gif) et sa dérivée est
et sa dérivée est 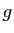 .
Or, pour tout
.
Or, pour tout
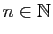 et pour tout
et pour tout
![$ x\in ]a,b[$](img186.gif) ,
,
Alors :
Or par hypothèse,
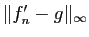 tend vers 0 :
tend vers 0 :
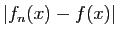 est majoré indépendamment de
est majoré indépendamment de  par un terme qui
tend vers 0. Donc la suite
par un terme qui
tend vers 0. Donc la suite 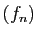 converge vers
converge vers  uniformément sur
uniformément sur ![$ ]a,b[$](img179.gif) .
. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
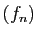 converge simplement vers
converge simplement vers  sur
sur
 si
si
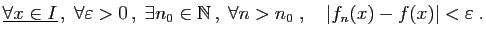
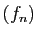 converge uniformément vers
converge uniformément vers  sur
sur
 si
si
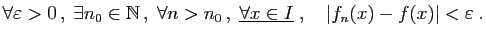
![]() tend vers 0, alors, pour tout
tend vers 0, alors, pour tout
![]() , il existe
, il existe ![]() tel que
tel que
![]() , donc pour tout
, donc pour tout ![]() ,
,
![]() .
. ![]() La figure 1 donne un support géométrique à
votre intuition. Si
La figure 1 donne un support géométrique à
votre intuition. Si ![]() converge uniformément vers
converge uniformément vers ![]() , alors
pour
, alors
pour ![]() assez grand, le graphe de
assez grand, le graphe de ![]() reste dans un «tube»
de largeur constante
reste dans un «tube»
de largeur constante
![]() autour du graphe de
autour du graphe de ![]() .
.
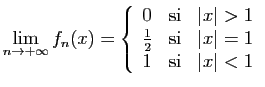
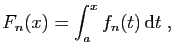
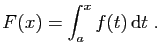
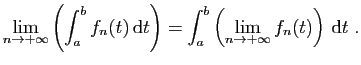
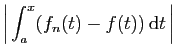
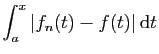
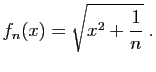
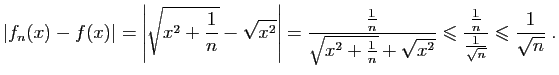
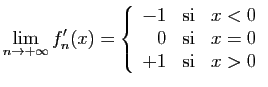
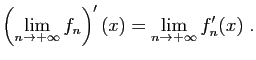
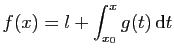 où
où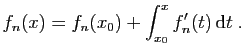
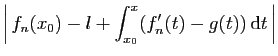
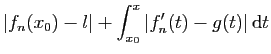
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales