Le résultat principal de cette section
est le théorème de Heine qui
affirme que toute fonction continue sur un intervalle fermé borné
est uniformément continue.
Il est utilisé en particulier
pour démontrer qu'une fonction continue est intégrable au sens de
Riemann, et nous vous
avons demandé de l'admettre dans le chapitre sur l'intégration.
Nous en profiterons aussi pour démontrer le théorème de Dini,
qui est une sorte de réciproque du
théorème 4. Nous commençons par le
théorème de Bolzano-Weierstrass, puis viendra le lemme de
Borel-Lebesgue, utilisé plusieurs fois dans les
démonstrations qui suivront. Les deux sont des cas particuliers
de résultats de topologie beaucoup plus généraux que vous
apprendrez plus tard.
Théorème 7 (de Bolzano-Weierstrass)
De toute suite de réels
bornée, on peut extraire une sous-suite convergente.
Démonstration : La démontration se fait par dichotomie.
Soit 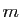 un minorant et
un minorant et 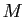 un majorant de la suite
un majorant de la suite 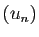 :
:
Posons 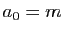 et
et 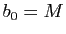 , et
, et
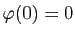 .
Divisons l'intervalle
.
Divisons l'intervalle ![$ [a_0,b_0]$](img201.gif) en deux,
et considérons les deux moitiés : l'une au moins contient une
infinité de termes de la suite
en deux,
et considérons les deux moitiés : l'une au moins contient une
infinité de termes de la suite 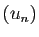 . Supposons que
. Supposons que
![$ [a_0,\frac{a_0+b_0}{2}]$](img202.gif) contienne une infinité de termes de la
suite. On note
contienne une infinité de termes de la
suite. On note 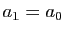 ,
,
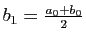 , et
, et
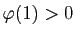 un
entier tel que
un
entier tel que
![$ u_{\varphi(1)}\in [a_1,b_1]$](img206.gif) . Si la première moitié
ne contient qu'un nombre fini de termes, on la remplace par l'autre
moitié
. Si la première moitié
ne contient qu'un nombre fini de termes, on la remplace par l'autre
moitié
![$ [\frac{a_0+b_0}{2},b_0]$](img207.gif) . On itère ensuite le
procédé, de manière à construire des intervalles
emboîtés
. On itère ensuite le
procédé, de manière à construire des intervalles
emboîtés ![$ [a_k,b_k]$](img208.gif) , de longueur
, de longueur 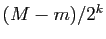 , et des valeurs
extraites
, et des valeurs
extraites
![$ u_{\varphi(k)}\in [a_k,b_k]$](img210.gif) . Les suites
. Les suites 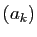 et
et 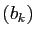 sont
adjacentes par construction, donc elles convergent vers la même
limite. Par le théorème des gendarmes
la suite
sont
adjacentes par construction, donc elles convergent vers la même
limite. Par le théorème des gendarmes
la suite
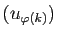 converge vers la
même limite que
converge vers la
même limite que 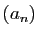 et
et 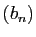 .
.  Le lemme de Borel-Lebesgue affirme que de tout recouvrement d'un
intervalle
Le lemme de Borel-Lebesgue affirme que de tout recouvrement d'un
intervalle ![$ [a,b]$](img159.gif) fermé borné, on peut extraire un
sous-recouvrement fini.
fermé borné, on peut extraire un
sous-recouvrement fini.
Démonstration : La première étape consiste à montrer que pour un
certain entier 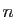 , tout intervalle de la forme
, tout intervalle de la forme
![$ ]y-1/n,y+1/n[$](img219.gif) est
inclus dans l'un des
est
inclus dans l'un des 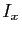 au moins.
au moins.
Ecrivons la négation :
Pour tout 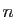 , soit
, soit 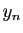 l'un des
l'un des 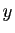 dont l'existence est affirmée
ci-dessus. Par le théorème de Bolzano-Weierstrass, on peut
extraire de la suite
dont l'existence est affirmée
ci-dessus. Par le théorème de Bolzano-Weierstrass, on peut
extraire de la suite 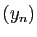 une sous-suite
une sous-suite
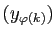 , qui
converge vers
, qui
converge vers ![$ c\in[a,b]$](img225.gif) . En particulier, aucun des intervalles
. En particulier, aucun des intervalles
![$ ]y_{\varphi(k)}-1/\varphi(k),y_{\varphi(k)}+1/\varphi(k)[$](img226.gif) n'est inclus dans
n'est inclus dans
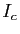 , ce qui est impossible si
, ce qui est impossible si 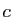 est la limite de
est la limite de
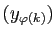 .
En utilisant la première étape, nous allons démontrer
le lemme par l'absurde : nous supposons donc qu'aucune réunion
finie des intervalles
.
En utilisant la première étape, nous allons démontrer
le lemme par l'absurde : nous supposons donc qu'aucune réunion
finie des intervalles 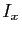 ne recouvre
ne recouvre ![$ [a,b]$](img159.gif) .
Fixons un entier
.
Fixons un entier 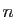 dont l'existence est affirmée ci-dessus.
Soit
dont l'existence est affirmée ci-dessus.
Soit 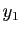 un point de
un point de ![$ [a,b]$](img159.gif) . Il
existe
. Il
existe 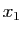 tel que
tel que
![$ ]y_1-1/n,y_1+1/n[\subset I_{x_1}$](img231.gif) . Comme
. Comme
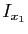 ne recouvre pas
ne recouvre pas ![$ [a,b]$](img159.gif) , il existe un point
, il existe un point 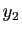 de
de ![$ [a,b]$](img159.gif) qui n'appartient pas à
qui n'appartient pas à 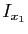 . Ce point est à distance au moins
. Ce point est à distance au moins
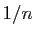 de
de 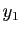 . Il existe un point
. Il existe un point 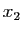 tel que
tel que
![$ ]y_2-1/n,y_2+1/n[\subset I_{x_2}$](img236.gif) . La réunion
. La réunion
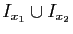 ne recouvre pas
ne recouvre pas ![$ [a,b]$](img159.gif) . Donc il existe
. Donc il existe 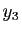 en dehors de
cette réunion :
en dehors de
cette réunion : 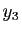 est à distance au moins
est à distance au moins 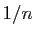 de
de 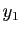 et
de
et
de 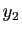 . Par récurrence, on construit ainsi une suite
. Par récurrence, on construit ainsi une suite 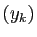 de points de
de points de ![$ [a,b]$](img159.gif) telle que deux quelconques de ses éléments sont
à distance au moins
telle que deux quelconques de ses éléments sont
à distance au moins 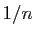 . En appliquant une fois de plus le
théorème de Bolzano-Weierstrass, une sous-suite de
. En appliquant une fois de plus le
théorème de Bolzano-Weierstrass, une sous-suite de 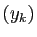 devrait
converger, d'où la contradiction.
devrait
converger, d'où la contradiction. La continuité uniforme est à la continuité ce que la convergence
uniforme est à la convergence simple (comparez avec la définition
1).
La continuité uniforme est à la continuité ce que la convergence
uniforme est à la convergence simple (comparez avec la définition
1).
Évidemment, la continuité uniforme implique la continuité
(simple), mais la
réciproque est fausse en général.
La différence entre les deux est subtile. Dans
la continuité simple, la valeur de 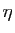 peut dépendre non seulement de
peut dépendre non seulement de
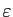 mais aussi de
mais aussi de  .
Dans la continuité uniforme, elle ne peut dépendre
que de
.
Dans la continuité uniforme, elle ne peut dépendre
que de
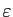 : pour un
: pour un
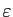 donné, on peut choisir le même
donné, on peut choisir le même
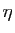 pour tous les points de l'intervalle.
pour tous les points de l'intervalle.
Examinons la fonction inverse sur ![$ I=]0,1]$](img242.gif) .
.
Soit  un point de
un point de ![$ ]0,1]$](img244.gif) et
et
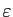 un réel strictement
compris entre 0 et
un réel strictement
compris entre 0 et 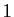 . L'image réciproque par
. L'image réciproque par  de
l'intervalle
de
l'intervalle
![$ [f(x)-\varepsilon ,f(x)+\varepsilon ]$](img245.gif) est l'intervalle :
est l'intervalle :
Cet intervalle contient  , et
, et
Posons
Alors, pour tout 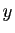 dans l'intervalle
dans l'intervalle
![$ [x-\eta_x,
x+\eta_x]$](img249.gif) ,
, 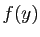 reste dans l'intervalle
reste dans l'intervalle
![$ [f(x)-\varepsilon ,f(x)+\varepsilon ]$](img245.gif) . De plus,
. De plus,
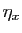 est le plus grand réel possédant cette
propriété. Observons que pour
est le plus grand réel possédant cette
propriété. Observons que pour
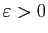 fixé,
fixé, 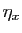 tend
vers 0 quand
tend
vers 0 quand  tend vers 0.
tend vers 0.
Bien sûr, pour n'importe quel
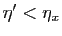 , l'implication
, l'implication
reste vraie. Mais il n'est pas possible de choisir un même 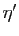 tel qu'elle reste vraie pour tous les
tel qu'elle reste vraie pour tous les  de
de ![$ ]0,1]$](img244.gif) : la
fonction
: la
fonction  n'est pas uniformément continue sur
n'est pas uniformément continue sur ![$ ]0,1]$](img244.gif) .
.
Examinons maintenant la fonction racine carrée sur le même
intervalle ![$ I=]0,1]$](img242.gif) .
.
Soit  un point de
un point de ![$ ]0,1]$](img244.gif) et
et
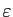 un réel strictement
compris entre 0 et
un réel strictement
compris entre 0 et 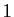 . Pour
. Pour
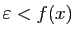 ,
l'image réciproque par
,
l'image réciproque par  de
l'intervalle
de
l'intervalle
![$ [f(x)-\varepsilon ,f(x)+\varepsilon ]$](img245.gif) est l'intervalle :
est l'intervalle :
Pour
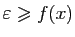 , c'est l'intervalle
, c'est l'intervalle
L'amplitude de ces intervalles dépend bien de  a priori.
Posons
a priori.
Posons
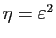 . Nous allons démontrer que pour tout
. Nous allons démontrer que pour tout
![$ x,y\in
]0,1]$](img261.gif) , si
, si
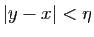 , alors
, alors
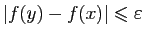 , ce qui entraîne que
, ce qui entraîne que  est uniformément continue sur
est uniformément continue sur  . Supposons
d'abord
. Supposons
d'abord
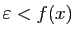 . Alors
. Alors
 . Donc
l'intervalle
. Donc
l'intervalle
![$ f^{-1}([f(x)-\varepsilon ,f(x)+\varepsilon ])$](img265.gif) contient l'intervalle
contient l'intervalle
![$ [x-\eta,x+\eta]$](img266.gif) : si
: si 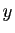 vérifie
vérifie
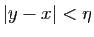 , alors
, alors
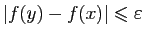 .
Supposons maintenant
.
Supposons maintenant
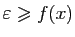 . Si
. Si 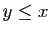 , alors
, alors
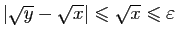 . Si
. Si
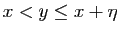 , alors
, alors
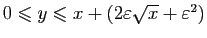 , donc
, donc
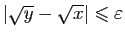 .
.
Théorème 8 (de Heine)
Toute fonction continue sur un intervalle fermé borné est
uniformément continue.
Donc la fonction
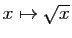 est uniformément continue sur
est uniformément continue sur
![$ [0,1]$](img149.gif) , tout comme la fonction
, tout comme la fonction
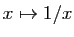 sur l'intervalle
sur l'intervalle
![$ [10^{-3},1]$](img274.gif) .
Démonstration : Soit
.
Démonstration : Soit ![$ [a,b]$](img159.gif) un intervalle fermé borné, et
un intervalle fermé borné, et  une fonction
continue sur
une fonction
continue sur ![$ [a,b]$](img159.gif) . Soit
. Soit
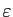 un réel strictement
positif. Puisque
un réel strictement
positif. Puisque  est continue sur
est continue sur ![$ [a,b]$](img159.gif) ,
pour tout
,
pour tout ![$ x\in [a,b]$](img164.gif) , il existe un
réel strictement positif, que nous noterons
, il existe un
réel strictement positif, que nous noterons 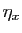 , tel que pour
tout
, tel que pour
tout
![$ y\in [a,b]$](img275.gif) ,
,
Pour tout  , considérons
l'intervalle ouvert
, considérons
l'intervalle ouvert
![$ ]x-\eta_x,x+\eta_x[$](img277.gif) , noté
, noté 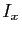 .
Par le lemme de Borel-Lebesque, on peut extraire de cette famille
d'intervalles un sous-recouvrement de
.
Par le lemme de Borel-Lebesque, on peut extraire de cette famille
d'intervalles un sous-recouvrement de ![$ [a,b]$](img159.gif) :
:
Puisque les intervalles ouverts
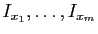 recouvrent
recouvrent
![$ [a,b]$](img159.gif) , il existe
, il existe 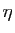 tel que si
tel que si
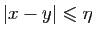 , alors
, alors  et
et 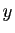 appartiennent à un même intervalle
appartiennent à un même intervalle 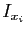 . Si c'est le cas,
. Si c'est le cas,
par définition de 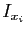 .
. La continuité uniforme est une notion générale. Nous en aurons
besoin plus loin pour
des fonctions de deux variables.
La continuité uniforme est une notion générale. Nous en aurons
besoin plus loin pour
des fonctions de deux variables.
Attention, il ne suffit pas que les applications partielles soient
continues sur  et
et 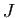 respectivement, pour
que
respectivement, pour
que  soit continue sur
soit continue sur 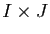 : voir le théorème
3.
Le théorème de Heine reste vrai pour un produit d'intervalles
fermés bornés (et plus généralement pour tout espace
topologique compact, comme vous l'apprendrez plus tard). Nous
l'utiliserons pour les fonctions de deux variables dans la section 1.5.
: voir le théorème
3.
Le théorème de Heine reste vrai pour un produit d'intervalles
fermés bornés (et plus généralement pour tout espace
topologique compact, comme vous l'apprendrez plus tard). Nous
l'utiliserons pour les fonctions de deux variables dans la section 1.5.
Théorème 9
Soient  et
et 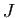 deux intervalles fermés bornés
de
deux intervalles fermés bornés
de
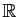 et
et
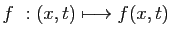 une
fonction continue sur
une
fonction continue sur 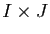 ,
à valeurs dans
,
à valeurs dans
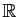 ou
ou
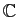 . Alors
. Alors  est uniformément
continue sur
est uniformément
continue sur 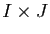 .
.
Démonstration : Fixons 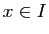 , et considérons l'application partielle
, et considérons l'application partielle
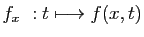 . On déduit immédiatement de la continuité
de
. On déduit immédiatement de la continuité
de  , que
, que 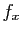 est continue sur
est continue sur 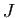 . D'après le théorème de
Heine, elle est donc uniformément continue sur
. D'après le théorème de
Heine, elle est donc uniformément continue sur 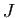 :
:
Écrivons de même que, pour tout 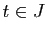 ,
l'application partielle
,
l'application partielle
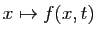 est
uniformément continue sur
est
uniformément continue sur  .
.
Le problème dans les écritures ci-dessus est que 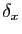 et
et
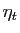 dépendent respectivement de
dépendent respectivement de  et
et 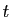 . Or nous devons
démontrer que la continuité est uniforme en les deux variables.
Posons :
. Or nous devons
démontrer que la continuité est uniforme en les deux variables.
Posons :
![$\displaystyle \forall x\in I ,\; I_x=]x-\delta_x,x+\delta_x[$](img295.gif)
et
![$\displaystyle \quad
\forall t\in J ,\; J_t=]t-\eta_t,t+\eta_t[
$](img296.gif)
D'après le lemme de Borel-Lebesgue, on peut extraire de ces
recouvrements des sous-recouvrements finis :
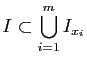
et
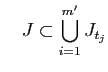
Puisque les intervalles ouverts
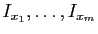 recouvrent
recouvrent
 , il existe
, il existe  tel que si
tel que si
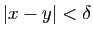 , alors
, alors  et
et 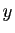 appartiennent au même intervalle
appartiennent au même intervalle 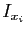 . De même, il existe
. De même, il existe
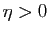 tel que si
tel que si
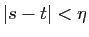 , alors
, alors 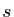 et
et 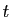 appartiennent au
même intervalle
appartiennent au
même intervalle 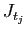 . On peut donc écrire :
. On peut donc écrire :
 Pour terminer cette section, voici une autre application du lemme de
Borel-Lebesgue. Le théorème de Dini affirme que si une suite
croissante de fonctions continues converge simplement vers une
fonction continue, alors la convergence est uniforme (comparez avec le
théorème 4).
Pour terminer cette section, voici une autre application du lemme de
Borel-Lebesgue. Le théorème de Dini affirme que si une suite
croissante de fonctions continues converge simplement vers une
fonction continue, alors la convergence est uniforme (comparez avec le
théorème 4).
Évidemment, le résultat vaut pour une suite décroissante,
en remplaçant 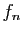 par
par 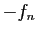 .
Démonstration : Fixons
.
Démonstration : Fixons
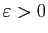 et
et
![$ x\in [a,b]$](img164.gif) . Puisque
. Puisque 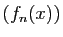 converge vers
converge vers
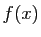 , il existe un entier
, il existe un entier 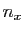 tel que
tel que
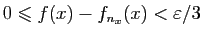 . Par continuité de
. Par continuité de  en
en  , il
existe
, il
existe 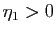 tel que si
tel que si
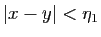 , alors
, alors
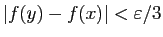 .
Par continuité de
.
Par continuité de 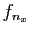 en
en  , il
existe
, il
existe 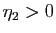 tel que si
tel que si
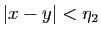 , alors
, alors
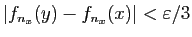 . Posons
. Posons
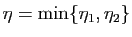 . Pour tout
. Pour tout
![$ y\in ]x-\eta,x+\eta[$](img323.gif) :
:
Notons 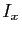 l'intervalle ouvert
l'intervalle ouvert
![$ ]x-\eta,x+\eta[$](img325.gif) . D'après le lemme
de Borel-Lebesgue, on peut extraire des
. D'après le lemme
de Borel-Lebesgue, on peut extraire des 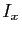 un sous-recouvrement
fini : il existe
un sous-recouvrement
fini : il existe
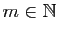 et
et
![$ x_1,\ldots,x_m\in [a,b]$](img326.gif) tels que
tels que
Notons 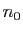 le plus grand des entiers
le plus grand des entiers
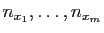 . Soit
. Soit
![$ y\in [a,b]$](img275.gif) : il existe
: il existe
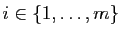 tel que
tel que
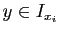 .
Puisque
.
Puisque
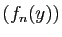 est une suite croissante, pour tout
est une suite croissante, pour tout
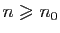 :
:
par définition de 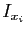 . Comme l'entier
. Comme l'entier 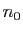 ne dépend pas de
ne dépend pas de
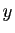 , la convergence est bien uniforme.
, la convergence est bien uniforme. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![$\displaystyle [a,b]\subset \bigcup_{i=1}^m I_{x_i}\;.$](img218.gif)
![]() .
.
![\begin{displaymath}
\begin{array}{rcl}
&f&\\
]0,1]&\longrightarrow&\mathbb{R}\\
x&\longmapsto&f(x)=1/x
\end{array}\end{displaymath}](img243.gif)
![$\displaystyle f^{-1}([f(x)-\varepsilon ,f(x)+\varepsilon ])=
\left[\frac{1}{f(x)+\varepsilon },\frac{1}{f(x)-\varepsilon }\right]
$](img246.gif)
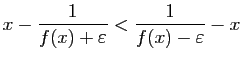
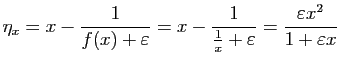
![]() , l'implication
, l'implication
![]() .
.
![\begin{displaymath}
\begin{array}{rcl}
&f&\\
]0,1]&\longrightarrow&\mathbb{R}\\
x&\longmapsto&f(x)=\sqrt{x}
\end{array}\end{displaymath}](img255.gif)
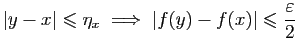
![$\displaystyle \exists m\in \mathbb{N} ,\;\exists x_1,\ldots,x_m\in[a,b]\;,\quad
[a,b]\subset \bigcup_{i=1}^m I_{x_i}
$](img278.gif)
![]() recouvrent
recouvrent
![]() , il existe
, il existe ![]() tel que si
tel que si
![]() , alors
, alors ![]() et
et ![]() appartiennent à un même intervalle
appartiennent à un même intervalle ![]() . Si c'est le cas,
. Si c'est le cas,
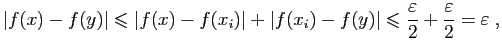
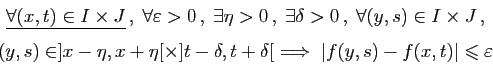
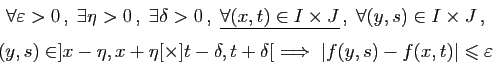
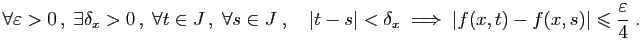
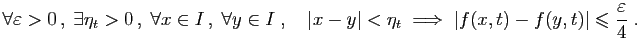
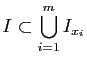 et
et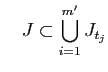
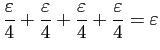
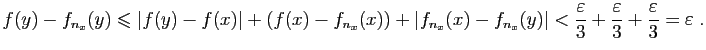
![$\displaystyle [a,b]\subset \bigcup_{i=1}^m I_{x_i}\;.$](img218.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales