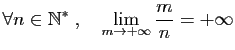 mais
mais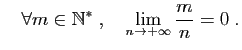
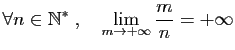 mais
mais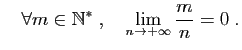
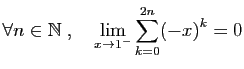 mais
mais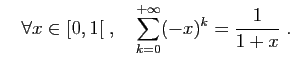
![$\displaystyle \forall n\in\mathbb{N}^*\;,\quad \int_0^1 n\mathbb{I}_{]0,\frac{1}{n}]}(x) \mathrm{d}x=1$](img20.gif) mais
mais
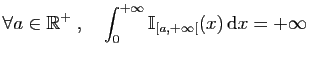 mais
mais
Alors les deux suites
![]() et
et
![]() convergent vers la même limite.
convergent vers la même limite.
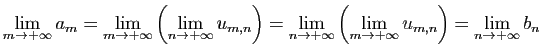
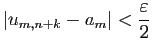 et
et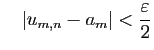
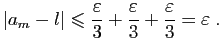
Alors la suite
![]() converge,
converge, ![]() admet une limite en
admet une limite en ![]() et les deux limites sont les mêmes.
et les deux limites sont les mêmes.
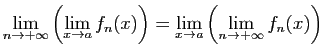
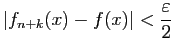 et
et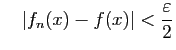
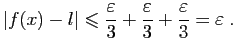
Alors ![]() admet une limite en
admet une limite en ![]() ,
, ![]() admet une limite en
admet une limite en ![]() et les deux limites sont les mêmes.
et les deux limites sont les mêmes.
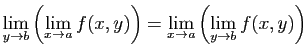
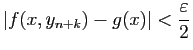 et
et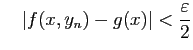
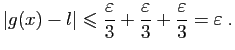
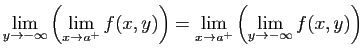
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales