Sachez donc qu'en chaque équation, autant que la quantité inconnue a de dimensions, autant il peut y avoir de diverses racines, c'est-à-dire de valeurs de cette quantité. [...]Qui parle de manière aussi péremptoire ? Descartes, en 1637. Il n'était pas le premier à le dire, tout polynôme de degré
Soit un multinôme quelconqueEuler et d'Alembert ont eu un mérite : celui d'être les premiers à se poser la question d'une démonstration. Euler en parle pour la première fois en 1742 dans une lettre à Nicolas Bernoulli, où il affirme que chaque polynôme à coefficients réels s'écrit comme un produit de monômes et de binômes à coefficients réels. Quelques mois plus tard, Euler annonce qu'il a trouvé une démonstration, mais qu'elle n'est «pas encore assez rigoureuse» Il présentera finalement cette démonstration le 10 novembre 1746. C'est le 6 décembre 1746 que d'Alembert envoie la sienne. Il indique en passant qu'Euler aurait «fait mention d'un ouvrage, où il a démontré en général la proposition dont il est question - ouvrage qui n'est pas encore publié». Encore de quoi alimenter une des nombreuses polémiques qui ont émaillé la vie des deux savants. Pour vous donner une idée du ton, voici un extrait d'une lettre d'Euler de 1757, à propos de d'Alembert., tel qu'il n'y ait aucune quantité réelle qui étant substituée à la place de
, y fasse évanouir tous les termes, je dis qu'il y aura toujours une quantité
à substituer à la place de
, et qui rendra ce multinôme égal à zéro.
Il avoit prétendu aussi que j'insérasse de nouvelles déclarations sur quantités d'articles que je lui avois volé. Mais ma patience est poussée à bout, et je lui ai fait répondre que je n'en ferois rien, et qu'il puisse publier lui-même ses prétentions partout où il veut, et que je ne m'y opposerois point. Il aura de quoi remplir l'article de prétention dans l'Encyclopédie.Les deux démonstrations d'Euler et d'Alembert étaient encore bien incomplètes selon nos critères. Voici ce qu'en disait Gauss en 1799, dans sa thèse (il était alors âgé de 22 ans).
Si on mène des opérations avec ces racines impossibles, comme si elles existaient, et si on dit par exemple, que la somme de toutes les racines de l'équationGauss donnera au cours de sa carrière 4 démonstrations différentes du théorème : celle de 1799, encore incomplète, deux en 1816 et une dernière en 1849, cinquante ans après la première ! Il ne fut pas le seul. Voici comment Cauchy introduit sa «Seconde note sur les racines imaginaires des équations», publiée au Bulletin de la Société Philomatique en 1817.est égale à
même si certaines d'entre elles peuvent être impossibles (ce qui signifie réellement : même si certaines sont non-existantes et donc manquantes), alors je ne peux que dire que je désapprouve totalement ce genre d'argument.
Qu'il soit toujours possible de décomposer un polynôme en produit de facteurs réels du premier et du second degré ; ou, en d'autres termes, que toute équation, dont le premier membre est une fonction rationnelle ou entière de la variableFort bien: le théorème pourrait donc s'appeler «théorème d'Euler-d'Alembert-Lagrange-Laplace-Gauss-Cauchy». Allons au plus simple : c'est le théorème fondamental de l'algèbre. Peut-être, sauf qu'il n'existe aucune justification purement algébrique. Toutes les démonstrations connues (et elles sont nombreuses), passent à un moment ou un autre par des arguments d'analyse. Celle que nous allons vous présenter n'utilise que les outils de ce chapitre. Nous allons commencer par étendre à des boules fermées dans, puisse toujours être vérifiée par des valeurs réelles ou imaginaires de cette variable : c'est une proposition que l'on a déjà prouvée de plusieurs manières. MM. Lagrange, Laplace et Gauss ont déjà employé diverses méthodes pour l'établir ; et j'en ai moi-même donné une démonstration fondée sur des considérations analogues à celles dont M. Gauss a fait usage.
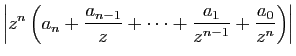 |
|||
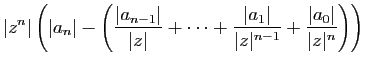 |
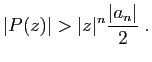
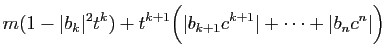 |
|||
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales