Il ne faut pas espérer qu'une série entière converge uniformément
sur tout
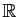 , voici pourquoi.
, voici pourquoi.
Proposition 5
La limite uniforme sur un intervalle non borné de
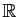 ,
d'une suite de polynômes est un polynôme.
,
d'une suite de polynômes est un polynôme.
Démonstration : Soit 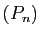 une suite de polynômes. Si elle converge uniformément
sur
une suite de polynômes. Si elle converge uniformément
sur  , elle est uniformément de Cauchy. Il existe
, elle est uniformément de Cauchy. Il existe 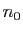 tel que
pour tout
tel que
pour tout 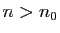 , et pour tout
, et pour tout 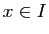 ,
,
Le polynôme
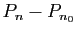 doit donc être borné sur
doit donc être borné sur  qui est non borné :
ce n'est possible que s'il est constant. Donc :
qui est non borné :
ce n'est possible que s'il est constant. Donc :
Soit  la limite de la suite
la limite de la suite 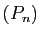 .
.
 Sur un intervalle fermé borné, la situation change radicalement.
Sur un intervalle fermé borné, la situation change radicalement.
Théorème 22 (de Weierstrass)
Toute fonction continue sur un intervalle fermé borné est limite
uniforme d'une suite de polynômes.
Ce magnifique résultat a fait l'objet de
toutes sortes de démonstrations, et de généralisations
(sous le nom de «Théorème de Stone-Weierstrass»).
C'est un théorème d'existence, qui ne dit rien a priori
sur la manière de construire la suite de polynômes qu'il affirme
exister. Il se trouve qu'il est possible de construire une telle
suite...
en jouant tout simplement à pile ou face.
Soit  une fonction continue de
une fonction continue de ![$ [0,1]$](img149.gif) dans
dans
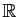 .
Soit
.
Soit ![$ x\in[0,1]$](img575.gif) , et supposez que vous disposiez d'une pièce
qui retourne «Pile» avec probabilité
, et supposez que vous disposiez d'une pièce
qui retourne «Pile» avec probabilité  . Si vous lancez la pièce
. Si vous lancez la pièce
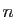 fois, le nombre de fois où vous obtenez «Pile» suit la loi
binomiale de paramètres
fois, le nombre de fois où vous obtenez «Pile» suit la loi
binomiale de paramètres 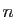 et
et  : il vaut
: il vaut
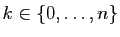 avec probabilité :
avec probabilité :
La loi des grands nombres (et votre bon sens) dit que si 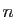 est grand,
le nombre de fois où vous tombez sur pile divisé par
est grand,
le nombre de fois où vous tombez sur pile divisé par 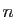 (la
fréquence), est proche
de
(la
fréquence), est proche
de  . En termes probabilistes, la loi de probabilité de la variable
aléatoire «fréquence de Pile» converge vers la masse de Dirac
en
. En termes probabilistes, la loi de probabilité de la variable
aléatoire «fréquence de Pile» converge vers la masse de Dirac
en  . Donc pour toute fonction
. Donc pour toute fonction  continue sur
continue sur ![$ [0,1]$](img149.gif) ,
,
Et voilà le travail ! Euh pas tout à fait quand même. La loi des grands
nombres n'affirme qu'une limite simple et il reste à démontrer
qu'elle est uniforme.
Démonstration : Comme entrée en matière,
vérifier que la somme des probabilités de la loi binomiale vaut 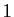 relève de la formule du binôme (d'où le nom).
relève de la formule du binôme (d'où le nom).
Vous savez peut être aussi que l'espérance de la loi
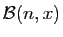 est
est 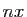 et que sa variance est
et que sa variance est 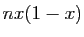 :
:
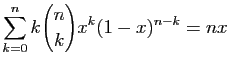
et
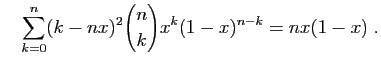
(Oubliez les probabilités, et redémontrez directement ces formules, c'est
un bon exercice).
Soit  une fonction continue sur
une fonction continue sur ![$ [0,1]$](img149.gif) . Elle est bornée : il existe
. Elle est bornée : il existe 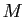 tel que
tel que
De plus, d'après le théorème de Heine,
elle est uniformément continue. Pour tout
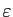 , il existe
, il existe 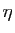 tel que
tel que
La différence entre  et son approximation
d'ordre
et son approximation
d'ordre 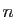 , s'exprime comme suit :
, s'exprime comme suit :
Notons cette somme 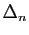 .
Nous la séparons en deux, en isolant les valeurs de
.
Nous la séparons en deux, en isolant les valeurs de 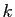 telles que
telles que
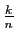 est proche de
est proche de  :
:
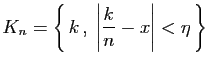
et
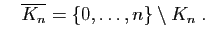
Il ne reste plus qu'à choisir 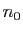 tel que pour tout
tel que pour tout 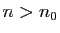 ,
,
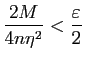 .
. Passer de l'intervalle
Passer de l'intervalle ![$ [0,1]$](img149.gif) à n'importe quel intervalle fermé borné
demande un simple changement de variable affine :
à n'importe quel intervalle fermé borné
demande un simple changement de variable affine :
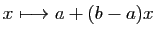 .
N'en déduisez pas pour autant que les polynômes de Bernstein soient une
bonne méthode pour calculer des approximations de fonctions. L'erreur en norme
uniforme sur
.
N'en déduisez pas pour autant que les polynômes de Bernstein soient une
bonne méthode pour calculer des approximations de fonctions. L'erreur en norme
uniforme sur ![$ [0,1]$](img149.gif) est de l'ordre de
est de l'ordre de
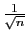 , ce qui
est bien plus mauvais que ce que l'on obtient avec les polynômes de Lagrange,
Hermite, Legendre, ou autres.
Bonne nouvelle, nous changeons de siècle : ce qui précède est paru
dans une petite note de deux pages (en français)
aux Communications de la Société Mathématique de Kharkov, volume 13, année 1912/13,
sous le titre «Démonstration du théorème de Weierstrass fondée sur le calcul des
probabilités». Pourquoi Sergueï Natanovitch Bernstein (1880-1968),
natif d'Odessa, écrivait-il en français à Kharkov ? D'une part parce qu'il avait
fait sa thèse à Paris (Hilbert et Picard au jury tout de
même...), d'autre part parce
que c'était encore un temps où une grande partie des scientifiques comprenaient
le français. Revenu en Russie, et malgré son parcours
parisien brillant, il avait dû passer un second doctorat à Kharkov
pour pouvoir y enseigner,
son diplôme étranger n'étant pas reconnu.
, ce qui
est bien plus mauvais que ce que l'on obtient avec les polynômes de Lagrange,
Hermite, Legendre, ou autres.
Bonne nouvelle, nous changeons de siècle : ce qui précède est paru
dans une petite note de deux pages (en français)
aux Communications de la Société Mathématique de Kharkov, volume 13, année 1912/13,
sous le titre «Démonstration du théorème de Weierstrass fondée sur le calcul des
probabilités». Pourquoi Sergueï Natanovitch Bernstein (1880-1968),
natif d'Odessa, écrivait-il en français à Kharkov ? D'une part parce qu'il avait
fait sa thèse à Paris (Hilbert et Picard au jury tout de
même...), d'autre part parce
que c'était encore un temps où une grande partie des scientifiques comprenaient
le français. Revenu en Russie, et malgré son parcours
parisien brillant, il avait dû passer un second doctorat à Kharkov
pour pouvoir y enseigner,
son diplôme étranger n'étant pas reconnu.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
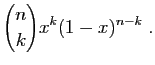
![$\displaystyle \forall x\in[0,1]\;,\quad f(x)=\lim_{n\to+\infty} \sum_{k=0}^n
f\left(\frac{k}{n}\right) \binom{n}{k}x^k(1-x)^{n-k} \;.
$](img945.gif)
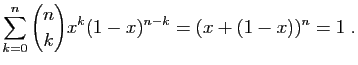
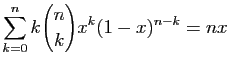 et
et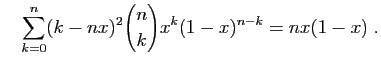
![$\displaystyle \forall x,y\in[0,1]\;,\quad \vert x-y\vert<\eta\;\Longrightarrow \vert f(x)-f(y)\vert<\frac{\varepsilon }{2}\;.
$](img953.gif)
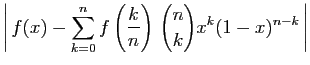
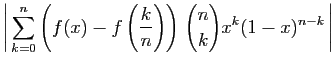
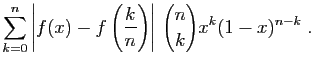
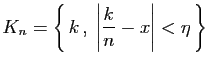 et
et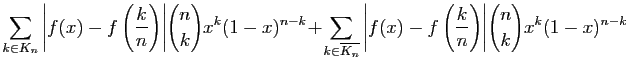
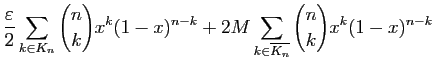
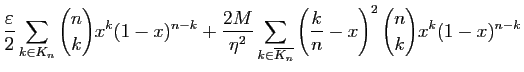
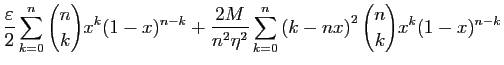
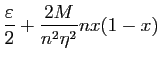
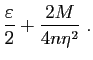
![]() tel que pour tout
tel que pour tout ![]() ,
,
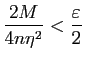 .
.![]() Passer de l'intervalle
Passer de l'intervalle ![]() à n'importe quel intervalle fermé borné
demande un simple changement de variable affine :
à n'importe quel intervalle fermé borné
demande un simple changement de variable affine :
![]() .
N'en déduisez pas pour autant que les polynômes de Bernstein soient une
bonne méthode pour calculer des approximations de fonctions. L'erreur en norme
uniforme sur
.
N'en déduisez pas pour autant que les polynômes de Bernstein soient une
bonne méthode pour calculer des approximations de fonctions. L'erreur en norme
uniforme sur ![]() est de l'ordre de
est de l'ordre de
![]() , ce qui
est bien plus mauvais que ce que l'on obtient avec les polynômes de Lagrange,
Hermite, Legendre, ou autres.
Bonne nouvelle, nous changeons de siècle : ce qui précède est paru
dans une petite note de deux pages (en français)
aux Communications de la Société Mathématique de Kharkov, volume 13, année 1912/13,
sous le titre «Démonstration du théorème de Weierstrass fondée sur le calcul des
probabilités». Pourquoi Sergueï Natanovitch Bernstein (1880-1968),
natif d'Odessa, écrivait-il en français à Kharkov ? D'une part parce qu'il avait
fait sa thèse à Paris (Hilbert et Picard au jury tout de
même...), d'autre part parce
que c'était encore un temps où une grande partie des scientifiques comprenaient
le français. Revenu en Russie, et malgré son parcours
parisien brillant, il avait dû passer un second doctorat à Kharkov
pour pouvoir y enseigner,
son diplôme étranger n'étant pas reconnu.
, ce qui
est bien plus mauvais que ce que l'on obtient avec les polynômes de Lagrange,
Hermite, Legendre, ou autres.
Bonne nouvelle, nous changeons de siècle : ce qui précède est paru
dans une petite note de deux pages (en français)
aux Communications de la Société Mathématique de Kharkov, volume 13, année 1912/13,
sous le titre «Démonstration du théorème de Weierstrass fondée sur le calcul des
probabilités». Pourquoi Sergueï Natanovitch Bernstein (1880-1968),
natif d'Odessa, écrivait-il en français à Kharkov ? D'une part parce qu'il avait
fait sa thèse à Paris (Hilbert et Picard au jury tout de
même...), d'autre part parce
que c'était encore un temps où une grande partie des scientifiques comprenaient
le français. Revenu en Russie, et malgré son parcours
parisien brillant, il avait dû passer un second doctorat à Kharkov
pour pouvoir y enseigner,
son diplôme étranger n'étant pas reconnu.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales