Theorema Egregium de Gauss

Le theorema egregium¹ est un important théorème de géométrie dû à Carl Friedrich Gauss (1977-1855) qui porte sur la courbure de Gauss des surfaces. Dans cette partie, on va essayer de comprendre ce que signifie ce théorème. On a vu dans la section 1.4 que la courbure de Gauss d'une surface en un point est le produit des deux courbures principales en ce point (Figure 16).

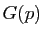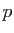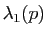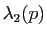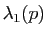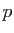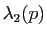Figure 16: La courbure de Gauss $G(p)$ au point $p$ est le produit des deux courbures principales $\lambda _1(p)$ et $\lambda _2(p)$ ( $\lambda _1(p)$ est la courbure de la courbe bleue au point $p$ et $\lambda _2(p)$ est la courbure de la courbe rouge au même point $p$).

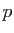Le Theorema egregium peut s'énoncer de la manière suivante :

Théorème 3   La courbure de Gauss d'une surface est invariante par isométrie locale.

Ce résultat nous indique que si on modifie une surface sans modifier ses longueurs, alors sa courbure de Gauss est inchangée. La courbure de Gauss est donc une courbure qui ne dépend pas de la forme de la surface, mais juste des distances mesurées sur cette surface.

Ce résultat est un résultat important de géométrie différentielle. On peut essayer de le comprendre au travers de l'exemple de l'hélicoïde et de la caténoïde. Une caténoïde et une hélicoïde sont représentées sur la Figure 17. Il est possible transformer la caténoïde en l'hélocoïde de manière continue et sans modifier les distance, comme illustré sur la Figure 18. Le théorème de Gauss implique alors que ces deux surfaces (qui sont isométriques) ont des courbures de Gauss identiques.

Figure 17: Caténoïde (à gauche) et hélicoïde (à droite) (source http://en.wikipedia.org/wiki/File:Helicatenoid.gif)

Figure 18: De la caténoïde a l'hélicoïde : la transformation se fait en conservant les distances (source http://en.wikipedia.org/wiki/File:Helicatenoid.gif)