Les courbes de Bézier sont des courbes paramétrées polynômiales qui ont été découvertes par l'ingénieur français Pierre Bézier (1910-1999) dans les années 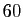 . Elles ont joué un rôle important dans le développement des logiciels de CAO, ont donné naissance à de nombreux objets mathématiques et sont encore utilisées dans des logiciels de dessin vectoriel. Pierre Bézier (pour plus de renseignements, on peu aussi regarder le site http://rocbo.lautre.net/bezier/pb-indus.htm) a travaillé chez Renault toute sa carrière. Une de ses préoccupation était de créer un moyen simple de modéliser des formes à partir de machines à commande numérique. L'idée lumineuse qu'il a eu consiste à exprimer une courbe comme combinaison linéaire de points (appelés points de contrôles). Ceci est bien illustré sur la Figure 14 : à gauche, on a des points (ordonnés); à droite, on a une courbe dont les extrémités sont deux points de cette courbe et qui est "attirée" par les autres points.
. Elles ont joué un rôle important dans le développement des logiciels de CAO, ont donné naissance à de nombreux objets mathématiques et sont encore utilisées dans des logiciels de dessin vectoriel. Pierre Bézier (pour plus de renseignements, on peu aussi regarder le site http://rocbo.lautre.net/bezier/pb-indus.htm) a travaillé chez Renault toute sa carrière. Une de ses préoccupation était de créer un moyen simple de modéliser des formes à partir de machines à commande numérique. L'idée lumineuse qu'il a eu consiste à exprimer une courbe comme combinaison linéaire de points (appelés points de contrôles). Ceci est bien illustré sur la Figure 14 : à gauche, on a des points (ordonnés); à droite, on a une courbe dont les extrémités sont deux points de cette courbe et qui est "attirée" par les autres points.
Figure 14:
Points de contrôles 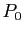 ,
, 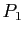 ,
, 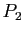 ,
, 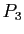 ,
, 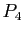 (à gauche) et courbe de Bézier associée (à droite)
(à gauche) et courbe de Bézier associée (à droite)
|
|
La définition de ces courbes est assez simple et utilise les polynômes de Bernstein. La courbe de Bézier associée à 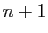 points
points
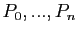 de
de
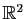 est la courbe paramétrée
est la courbe paramétrée
![$ P:[0,1]\to\mathbb{R}^2$](img715.gif) donnée pour tout
donnée pour tout
![$ t\in [0,1]$](img516.gif) par :
par :
où 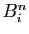 est le polynôme de Bernstein
est le polynôme de Bernstein
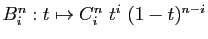 .
La courbe de Bézier a des propriétés assez sympathiques :
.
La courbe de Bézier a des propriétés assez sympathiques :
- Elle a pour extrémités les points
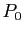 et
et 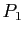 (
(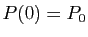 et
et 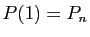 ).
).
- Le vecteur
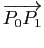 est tangent à la courbe de Bézier au point de paramètre
est tangent à la courbe de Bézier au point de paramètre 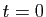 .
.
- Le vecteur
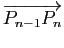 est tangent à la courbe de Bézier au point de paramètre
est tangent à la courbe de Bézier au point de paramètre 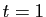 .
.
- La courbe est "attirée" par les points
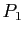 ,...,
,...,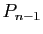 (cette propriété est précisée ci-dessous).
(cette propriété est précisée ci-dessous).
- La courbe de Bézier ne dépend pas du repère choisi. Si on effectue une rotation des points de contrôles, la forme de la courbe de Bézier reste la même.
Les points
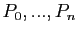 sont appelés points de contrôles de la courbe de Bézier, ce qui est assez naturel. En effet, la courbe dépend de ces points. Quand on les bouge, on modifie la courbe qui est "attirée" par ces points. Plus précisément, chaque point
sont appelés points de contrôles de la courbe de Bézier, ce qui est assez naturel. En effet, la courbe dépend de ces points. Quand on les bouge, on modifie la courbe qui est "attirée" par ces points. Plus précisément, chaque point 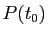 de la courbe de Bézier est combinaison linéaire des points de contrôles
de la courbe de Bézier est combinaison linéaire des points de contrôles 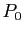 ,...,
,...,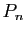 :
:
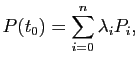
avec
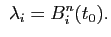
En fait, les propriétés sympathiques des courbes de Bézier proviennent de propriétés sur les polynômes de Bernstein, comme par exemple celle de la partition de l'unité :
On peut remarquer que cette propriété implique que le point 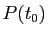 dans la formule ci-dessus est barycentre des points
dans la formule ci-dessus est barycentre des points 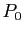 ,...,
,...,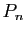 .
.
Figure 15:
Polynômes de Bernstein dans le cas 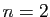 (à gauche),
(à gauche), 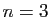 (au milieu) et
(au milieu) et 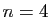 (à droite)
(à droite)
|
|
Les courbes de Bézier forment un outil de base qui est utilisé pour définir d'autres notions utiles en modélisation. C'est le cas par exemple des courbes B-splines, beaucoup utilisées dans les logiciels de dessin, qui sont des courbes obtenues en mettant "bout à bout" des courbes de Bézier.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() points
points
![]() de
de
![]() est la courbe paramétrée
est la courbe paramétrée
![]() donnée pour tout
donnée pour tout
![]() par :
par :
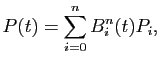
![]() sont appelés points de contrôles de la courbe de Bézier, ce qui est assez naturel. En effet, la courbe dépend de ces points. Quand on les bouge, on modifie la courbe qui est "attirée" par ces points. Plus précisément, chaque point
sont appelés points de contrôles de la courbe de Bézier, ce qui est assez naturel. En effet, la courbe dépend de ces points. Quand on les bouge, on modifie la courbe qui est "attirée" par ces points. Plus précisément, chaque point ![]() de la courbe de Bézier est combinaison linéaire des points de contrôles
de la courbe de Bézier est combinaison linéaire des points de contrôles ![]() ,...,
,...,![]() :
:
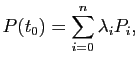 avec
avec![$\displaystyle \forall t \in [0,1]\quad \sum_{i=1}^nB^n_i(t)=1.
$](img727.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales