On vérifie immédiatement que si deux fonctions
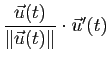 .
.
Une fonction
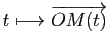 de
de
Rappels : dérivation vectorielle
Soit
![]() une fonction d'un intervalle
une fonction d'un intervalle ![]() de
de
![]() dans un espace vectoriel
dans un espace vectoriel
![]() de dimension finie
de dimension finie ![]() . On dit que cette fonction est dérivable si toutes les coordonnées
. On dit que cette fonction est dérivable si toutes les coordonnées
![]() de
de ![]() dans une base
dans une base
![]() de
de
![]() le sont (cette propriété ne dépend pas de la base). Le vecteur
le sont (cette propriété ne dépend pas de la base). Le vecteur
![]() est alors indépendant de la base. On le note
est alors indépendant de la base. On le note ![]() .
.
On vérifie immédiatement que si deux fonctions
![]() et
et
![]() d'un intervalle
d'un intervalle ![]() de
de
![]() dans un espace vectoriel euclidien
dans un espace vectoriel euclidien
![]() sont dérivables, la fonction
sont dérivables, la fonction
![]() de
de ![]() dans
dans
![]() est dérivable et que sa dérivée est
est dérivable et que sa dérivée est
![]() .
En particulier, la fonction
.
En particulier, la fonction
![]() a pour dérivée
a pour dérivée
![]() . On en déduit (dérivation d'une fonction composée) que la fonction
. On en déduit (dérivation d'une fonction composée) que la fonction
![]() est dérivable en tout point où elle ne s'annule pas et que sa dérivée en un tel point est égale à
est dérivable en tout point où elle ne s'annule pas et que sa dérivée en un tel point est égale à
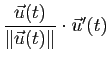 .
.
Une fonction
![]() d'un intervalle
d'un intervalle ![]() de
de
![]() dans un espace affine
dans un espace affine ![]() est dite dérivable s'il existe un point
est dite dérivable s'il existe un point ![]() de
de ![]() tel que la fonction
tel que la fonction
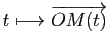 de
de ![]() dans
dans
![]() soit dérivable. On note alors
soit dérivable. On note alors
![]() sa dérivée (il résulte immédiatement de la relation de Chasles que ce vecteur ne dépend pas du point
sa dérivée (il résulte immédiatement de la relation de Chasles que ce vecteur ne dépend pas du point ![]() ). La courbe de représentation paramétrique
). La courbe de représentation paramétrique
![]() admet alors en tout point de paramètre
admet alors en tout point de paramètre ![]() où
où
![]() ne s'annule pas une tangente de vecteur directeur
ne s'annule pas une tangente de vecteur directeur
![]() .
.
Tangentes à la parabole
![\includegraphics[width=0.5\textwidth]{tangenteparabole}](img182.gif)
Soit ![]() une représentation paramétrique de la parabole et
une représentation paramétrique de la parabole et ![]() le projeté orthogonal de
le projeté orthogonal de ![]() sur la directrice
sur la directrice ![]() . En dérivant par rapport à
. En dérivant par rapport à ![]() la relation
la relation
![]() , on obtient
, on obtient
![]() . Mais
. Mais
![]() puisque le vecteur
puisque le vecteur
![]() est orthogonal à
est orthogonal à ![]() et le vecteur
et le vecteur
![]() appartient à la direction de
appartient à la direction de ![]() . Il en résulte
. Il en résulte
![]() . La tangente en
. La tangente en ![]() à la parabole est donc orthogonale à la droite
à la parabole est donc orthogonale à la droite ![]() , i.e. est la hauteur issue de
, i.e. est la hauteur issue de ![]() dans le triangle
dans le triangle ![]() . Ce triangle étant isocèle en
. Ce triangle étant isocèle en ![]() , cette tangente est aussi la médiatrice de
, cette tangente est aussi la médiatrice de ![]() et la bissectrice intérieure de l'angle en
et la bissectrice intérieure de l'angle en ![]() de ce triangle.
de ce triangle.
Il en résulte que tout rayon lumineux parallèle à l'axe d'un miroir parabolique se réfléchit en un rayon passant par le foyer : un miroir parabolique concentre donc la lumière au foyer. Cette propriété est utilisée dans certains télescopes et dans les fours solaires (voir section 3.4).
![\includegraphics[width=0.5\textwidth]{miroir}](img195.gif)
Tangentes aux coniques à centre
Soit ![]() l'ellipse de foyers
l'ellipse de foyers ![]() et
et ![]() et de demi-grand axe
et de demi-grand axe ![]() . En dérivant la relation
. En dérivant la relation ![]() , on obtient de même :
, on obtient de même :
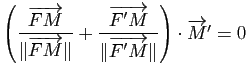 . Mais le vecteur
. Mais le vecteur
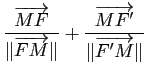 est somme de deux vecteurs directeurs unitaires des demi-droites
est somme de deux vecteurs directeurs unitaires des demi-droites ![]() et
et ![]() ; c'est donc un vecteur directeur de la bissectrice intérieure de l'angle en
; c'est donc un vecteur directeur de la bissectrice intérieure de l'angle en ![]() du triangle
du triangle ![]() . Il en résulte que la tangente en
. Il en résulte que la tangente en ![]() à l'ellipse est orthogonale à cette bissectrice intérieure : c'est donc la bissectrice extérieure de l'angle en
à l'ellipse est orthogonale à cette bissectrice intérieure : c'est donc la bissectrice extérieure de l'angle en ![]() de ce triangle.
de ce triangle.
Dans le cas de l'hyperbole, on montre de même, en dérivant la relation
![]() (chaque choix de signe correspondant à une branche de l'hyperbole), que la tangente en
(chaque choix de signe correspondant à une branche de l'hyperbole), que la tangente en ![]() est la bissectrice intérieure de l'angle en
est la bissectrice intérieure de l'angle en ![]() du triangle
du triangle ![]() .
.
![\includegraphics[width=0.45\textwidth]{tangenteellipse1}](img204.gif)
![\includegraphics[width=0.45\textwidth]{tangentehyperbole1}](img205.gif)
Ellipses et hyperboles homofocales
Les ellipses (resp. les hyperboles) de foyers ![]() et
et ![]() fixés sont les lignes de niveau de la fonction
fixés sont les lignes de niveau de la fonction
![]() (resp.
(resp.
![]() ). Par tout point du plan n'appartenant pas au segment
). Par tout point du plan n'appartenant pas au segment ![]() (resp. à la médiatrice de
(resp. à la médiatrice de ![]() ou à la droite
ou à la droite ![]() privée du segment
privée du segment ![]() ) passe donc une et une seule ellipse (resp. hyperbole) de foyers
) passe donc une et une seule ellipse (resp. hyperbole) de foyers ![]() et
et ![]() . Il résulte de la démonstration précédente que ces deux coniques se coupent à angle droit, puisque les deux bissectrices en
. Il résulte de la démonstration précédente que ces deux coniques se coupent à angle droit, puisque les deux bissectrices en ![]() du triangle
du triangle ![]() sont perpendiculaires (les gradients des deux fonctions considérées sont en tout point orthogonaux). Les ellipses et les hyperboles de foyers fixés constituent donc deux familles de courbes orthogonales.
sont perpendiculaires (les gradients des deux fonctions considérées sont en tout point orthogonaux). Les ellipses et les hyperboles de foyers fixés constituent donc deux familles de courbes orthogonales.
![\includegraphics[width=0.6\textwidth]{homo}](img210.gif)
La figure GeoGebra illustre ce résultat. Vous pouvez déplacer le point ![]() . L'ellipse et l'hyperbole de foyers
. L'ellipse et l'hyperbole de foyers ![]() et
et ![]() passant par
passant par ![]() sont représentées.
sont représentées.
Génération tangentielle des coniques
Soit ![]() une droite du plan et
une droite du plan et ![]() un point du plan n'appartenant pas à
un point du plan n'appartenant pas à ![]() . L'ensemble des médiatrices des segments
. L'ensemble des médiatrices des segments ![]() , quand
, quand ![]() parcourt
parcourt ![]() est alors l'ensemble des tangentes à la parabole de foyer
est alors l'ensemble des tangentes à la parabole de foyer ![]() et de directrice
et de directrice ![]() . On dit que la parabole est l'enveloppe de cette famille de droites.
. On dit que la parabole est l'enveloppe de cette famille de droites.
La figure GeoGebra illustre ce résultat. Vous pouvez déplacer le point ![]() sur la directrice
sur la directrice ![]() . La trace de la médiatrice du segment
. La trace de la médiatrice du segment ![]() est représentée.
est représentée.
De même, si ![]() et
et ![]() sont deux points distincts du plan et
sont deux points distincts du plan et ![]() le cercle de centre
le cercle de centre ![]() et de rayon
et de rayon ![]() , où
, où ![]() est un réel vérifiant
est un réel vérifiant ![]() , l'ensemble des médiatrices des segments
, l'ensemble des médiatrices des segments ![]() , quand
, quand ![]() parcourt
parcourt ![]() est l'ensemble des tangentes à l'ellipse de foyers
est l'ensemble des tangentes à l'ellipse de foyers ![]() et
et ![]() et de grand axe
et de grand axe ![]() . L'ellipse est donc l'enveloppe de cette famille de droites. Le cas de l'hyperbole est analogue (avec cette fois
. L'ellipse est donc l'enveloppe de cette famille de droites. Le cas de l'hyperbole est analogue (avec cette fois ![]() ).
).
![\includegraphics[width=0.6\textwidth]{enveloppe}](img216.gif)
Les deux figures GeoGebra illustrent cette propriété dans le cas de l'ellipse et de l'hyperbole résultat. Vous pouvez déplacer le point ![]() sur le cercle directeur de centre
sur le cercle directeur de centre ![]() . La trace de la médiatrice du segment
. La trace de la médiatrice du segment ![]() est représentée.
est représentée.
Cas de l'ellipse :
Cas de l'hyperbole :
Si vous préférez une version animée, vous pouvez regarder les deux figures ci-dessous :
Cas de l'ellipse :
Cas de l'hyperbole :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales