Section : Cours
Avant : Définition par foyer et directrice
Après : Propriétés des tangentes

Définition bifocale des coniques à centre

L'existence de deux couples foyer-directrice pour les coniques à centre permet d'en obtenir une autre caractérisation. Si on appelle en effet $ F$ et $ F'$ les foyers, $ D$ et $ D'$ les directrices correspondantes, $ H$ et $ H'$ les projetés d'un point $ M$ de la conique sur $ D$ et $ D'$, on a les relations $ MF=eMH$, $ MF'=eMH'$.

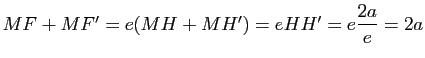Cas de l'ellipse L'ellipse est entièrement incluse dans la bande verticale délimitée par ses deux directrices ; il en résulte que tout point $ M$ de l'ellipse appartient au segment $ HH'$, d'où $ MF+MF'=e(MH+MH')=eHH'=e\dfrac{2a}{e}=2a$. L'ellipse est donc incluse dans l'ensemble des points $ M$ du plan vérifiant $ MF+MF'=2a$.
Réciproquement, si un point $ M$ du plan de coordonnées $ (x,y)$ vérifie $ MF+MF'=2a$, on déduit de la relation

$\displaystyle (MF-MF')(MF+MF')=MF^2-MF'^2=[(x-c)^2+y^2]-[(x+c)^2+y^2]=-4cx$

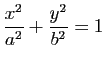que $ MF-MF'=-2 e x$, puisque $ e=c/a$, d'où $ MF=a-ex$, et $ MF^2=(x-c)^2+y^2=(a-ex)^2$, soit $ x^2 (1-e^2)+y^2=b^2$ puisque $ ea=c$ et $ a^2-b^2=c^2$, ou encore, en divisant par $ b^2$, $ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, ce qui montre que l'ensemble des points $ M$ du plan vérifiant $ MF+MF'=2a$ est inclus dans l'ellipse. L'ellipse est donc égale à cet ensemble.

\includegraphics[width=6cm]{bifocale1} \includegraphics[width=6cm]{bifocale2}

Cas de l'hyperbole

L'hyperbole se compose au contraire de deux branches extérieures à la bande verticale délimitée par ses deux directrices. Il en résulte que pour tout point $ M$ de l'hyperbole, on a $ \vert MF-MF'\vert=e\vert MH-MH'\vert=2a$. L'une des branches de l'hyperbole est donc incluse dans l'ensemble des points $ M$ du plan vérifiant $ MF-MF'=2a$ et l'autre dans l'ensemble des points $ M$ vérifiant $ MF'-MF=2a$. Un calcul identique à celui opéré dans le cas de l'ellipse permet ici encore de vérifier que l'hyperbole est exactement l'ensemble des points $ M$ du plan vérifiant $ \vert MF-MF'\vert=2a$.

En résumé :

Proposition 3   Soient $ F$ et $ F'$ deux points distincts du plan et $ c=FF'/2$ la demi-distance entre ces deux points.
  1. Pour tout réel $ a>c$, l'ensemble des points $ M$ du plan vérifiant $ MF+MF'=2a$ est l'ellipse de foyers $ F$ et $ F'$ et de grand axe $ 2a$.
  2. Pour tout réel positif $ a<c$, l'ensemble des points $ M$ du plan vérifiant $ \vert MF-MF'\vert=2a$ est l'hyperbole de foyers $ F$ et $ F'$ et de grand axe $ 2a$.

Le cercle peut apparaître ici encore comme un cas particulier d'ellipse pour laquelle les deux foyers seraient confondus.

Application : construction de l'ellipse par le procédé dit du jardinier.

Pour tracer une ellipse de foyers $ F$ et $ F'$ et de longueur de grand axe $ 2a>FF'$ donnés, il suffit de fixer deux piquets en $ F$ et $ F'$ et d'y attacher les extrémités d'une ficelle non élastique de longueur $ 2a$. Le trajet que l'on parcourt en tournant autour de $ F$ et $ F'$ tout en maintenant la ficelle tendue est l'ellipse cherchée.

\includegraphics[width=0.5\textwidth]{jardinier}


Tableau 1: Coniques à centre
  Ellipse Hyperbole
Équation réduite
$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
$ 0<b<a$
$ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$
Représentation paramétrique
$ x=a\cos t$
$ y=b\sin t$
$ 0\leq t <2\pi$
$ x=\varepsilon a\ch t$
$ y=b\sh t$
$ \varepsilon\in\{-1,+1\},\, t\in\mathbb{R}$
Distance focale
$ FF'=2c$
$ a^2=b^2+c^2$
$ FF'=2c$
$ c^2=a^2+b^2$
Excentricité $ e=\dfrac{c}{a}$ $ e=\dfrac{c}{a}$
Longueur des axes
$ AA'=2a$    grand axe
$ BB'=2b$    petit axe
$ AA'=2a$    axe focal
Définition bifocale $ MF+MF'=2a$ $ \vert\, MF-MF'\,\vert=2a$



Section : Cours
Avant : Définition par foyer et directrice
Après : Propriétés des tangentes


         © UJF Grenoble, 2011                              Mentions légales