Ellipse et cercle

Définition 2 Soit une droite du plan et $\lambda$ un réel non nul. On appelle affinité orthogonale de base et de rapport $\lambda$ l'application du plan dans lui-même qui à tout point associe le point défini par $\overrightarrow{mM'}=\lambda \, \overrightarrow{mM}$ , où est le projeté orthogonal du point sur la droite .

Si on rapporte le plan à un repère orthonormé $(O,\vec{i},\vec{j})$ tel que le point

appartienne à

et que $\vec{i}$ soit un vecteur directeur de

, les coordonnées du point

sont données par

, $y'=\lambda y$ , où

sont les coordonnées de

Une affinité orthogonale est une transformation affine. Elle conserve donc l'alignement, les milieux, le contact (ce qui signifie qu'elle transforme la tangente à une courbe en la tangente à la courbe image), et multiplie les aires par la valeur absolue du déterminant de sa partie linéaire, qui est ici le rapport de l'affinité. Elle laisse par ailleurs fixe tout point de sa base

Proposition 5 L'ellipse de représentation paramétrique $x=a\cos t$ , $y=b\sin t$ dans un repère orthonormal $(O,\vec{i},\vec{j})$ est l'image du cercle de centre et de rayon par l'affinité orthogonale de base et de rapport . Ce cercle est appelé cercle principal de l'ellipse.

Elle est aussi l'image du cercle de centre et de rayon par l'affinité orthogonale de base et de rapport . Ce cercle est appelé cercle secondaire de l'ellipse.

Démonstration : Il suffit d'utiliser la représentation paramétrique $x=a\cos t$ , $y=a\sin t$ (resp. $x=b\cos t$ , $y=b\sin t$ ) du cercle principal (resp. secondaire) de l'ellipse. $\square$

Cette propriété permet de déduire un certain nombre de propriétés de l'ellipse de propriétés analogues pour le cercle.

Pour construire à la règle et au compas un point

de l'ellipse connaissant ses axes et ses cercles principal et secondaire, il suffit de tracer une demi-droite $\Delta$ d'origine le centre

de l'ellipse ; soit

le point d'intersection de $\Delta$ avec le cercle principal,

le point d'intersection de $\Delta$ avec le cercle secondaire ; la parallèle au grand axe mené par par

et la parallèle au petit axe menée par

se coupent un point

de l'ellipse. Le paramètre

de ce point dans la représentation paramétrique $x=a\cos t, \; y=b \sin t$ est une mesure de l'angle $(Ox,\Delta)$ et est appelé anomalie excentrique du point

Pour construire la tangente en

à l'ellipse, il suffit de tracer la tangente au cercle principal en

; si elle coupe le grand axe en

, la droite

est tangente à l'ellipse en

. On peut aussi construire le point d'intersection

de la tangente en

au cercle secondaire avec le petit axe ; les trois points

sont alors alignés sur cette tangente.

On appelle corde d'une conique $\Gamma$ tout segment joignant deux points de $\Gamma$ et diamètre d'une conique à centre toute corde passant par le centre de cette conique.

Proposition 6 Soit une ellipse et une droite.

L'ensemble des milieux des cordes de parallèles à est le diamètre de ayant pour extrémités les deux points et de en lesquels la tangente à est parallèle à .
L'ensemble des milieux des cordes de parallèles à est le diamètre de parallèle à .
Les diamètres et de sont dits conjugués.

Démonstration : Le parallélisme et les milieux sont conservés par toute affinité orthogonale. Il suffit donc de prendre l'image de

par l'affinité orthogonale de base le grand axe qui transforme

en son cercle principal

et de démontrer la propriété pour

. Mais la propriété est évidente dans le cas d'un cercle, puisque l'ensemble des milieux des cordes d'un cercle parallèles à une droite donnée est le diamètre du cercle orthogonal à cette droite. $\square$

On remarquera que deux diamètres conjugués d'une ellipse ne sont en général pas orthogonaux : en effet une affinité orthogonale ne conserve pas l'orthogonalité.

La figure GeoGebra représente un cercle et l'ellipse image de ce cercle par une affinité orthogonale. Vous pouvez faire varier le rapport de l'affinité et déplacer le point sur le cercle. Les deux diamètres orthogonaux de ce cercle sont transformés par l'affinité en deux diamètres conjugués de l'ellipse.
C'est une appliquette Java créée avec GeoGebra ( www.geogebra.org) - Il semble que Java ne soit pas installé sur votre ordinateur, merci d'aller sur www.java.com Aire de l'ellipse

Démonstration : Une affinité orthogonale de rapport

multiplie les aires par

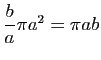. L'aire intérieure à l'ellipse est donc $\dfrac{b}{a} \pi a^2=\pi a b$ . $\square$

Sur un segment

de longueur

(

), on place un point

tel que

(et donc

). Quand

se déplacent respectivement sur deux axes orthogonaux

, le point

décrit un quart d'ellipse.

Démonstration : Soit

tel que le quadrilatère

soit un parallélogramme et

l'intersection de

(i.e. le projeté orthogonal de

sur

). Les triangles rectangles

étant semblables, le point

se déduit du point

par l'affinité orthogonale de base

et de rapport $-\dfrac{b}{a}$ . Mais le point

décrit un quart de cercle de centre

et de rayon

. $\square$

Proposition 8 Le projeté orthogonal d'un cercle de rayon de l'espace sur un plan est :

un cercle de rayon si le plan est parallèle au plan de ;
un segment de longueur si le plan est perpendiculaire au plan de ;
une ellipse de demi-grand axe et de demi-petit axe $R\cos \theta$ , où $\theta$ est l'angle du plan avec le plan de si ce plan n'est ni parallèle ni perpendiculaire à .

Démonstration : Si deux plans sont parallèles, le projeté orthogonal d'une figure sur l'un se déduit du projeté orthogonal de cette figure sur l'autre par une translation. Quitte à compléter par une translation, on peut donc supposer que le plan

passe par le centre

Soit

le plan de

. Le cas où

sont parallèles est immédiat. Supposons donc

sécants. Soit $(O,\vec{i},\vec{j},\vec{k})$ un repère orthonormé de l'espace tel que $\vec{i}$ soit un vecteur directeur de la droite

d'intersection de

et $\vec{j}$ un vecteur de

. Soit $\u$ un vecteur unitaire de

orthogonal à $\vec{i}$ ; $(O,\vec{i},\u)$ est alors un repère orthonormé de

. Le cercle

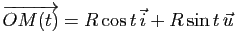
admet dans ce repère la représentation paramétrique $\overrightarrow{OM(t)}=R\cos t \, \vec{i}+ R\sin t \, \u$ $(0\leq t\leq 2\pi)$ . Les composantes du vecteur $\u$ dans la base $(\vec{i},\vec{j},\vec{k})$ sont (quitte à changer le sens de $\vec{j}$ et $\vec{k}$ ) $(0,\cos \theta, \sin\theta)$ . Il en résulte que