Voici deux systèmes linéaires d'équations.
Voici deux systèmes linéaires d'équations de récurrence.
Voici deux systèmes linéaires d'équations différentielles.
Les trois problèmes, de natures très différentes, ont en commun
leur écriture matricielle, avec les deux matrices suivantes.
Tous les problèmes linéaires sont plus faciles à résoudre quand
la matrice est diagonale !
Il se trouve que les deux matrices 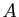 et
et 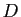 sont
semblables, c'est-à-dire qu'elles représentent
le même endomorphisme dans deux bases
différentes, ou encore, il existe une matrice de passage
sont
semblables, c'est-à-dire qu'elles représentent
le même endomorphisme dans deux bases
différentes, ou encore, il existe une matrice de passage 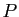 telle que
telle que
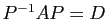 .
.
Définition 8
Une matrice
carrée
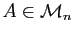 est diagonalisable si elle est
semblable à une matrice diagonale, c'est-à-dire s'il existe une
matrice de passage
est diagonalisable si elle est
semblable à une matrice diagonale, c'est-à-dire s'il existe une
matrice de passage 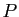 telle que
telle que
Les techniques permettant de savoir si une matrice donnée est
diagonalisable et de calculer la matrice de passage 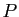 si elle l'est,
dépassent le cadre de ce cours. On commence par calculer
les coefficients diagonaux de
si elle l'est,
dépassent le cadre de ce cours. On commence par calculer
les coefficients diagonaux de 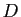 , qui sont les
valeurs de
, qui sont les
valeurs de 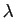 telles que
telles que
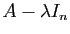 n'est pas inversible :
on les appelle les valeurs propres, et leur ensemble est le
spectre de la matrice. Pour chaque valeur propre
n'est pas inversible :
on les appelle les valeurs propres, et leur ensemble est le
spectre de la matrice. Pour chaque valeur propre 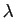 , on
détermine ensuite le sous-espace propre associé à
, on
détermine ensuite le sous-espace propre associé à
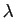 : c'est l'ensemble des vecteurs
: c'est l'ensemble des vecteurs 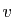 tels que
tels que
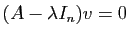 . La matrice est diagonalisable lorsqu'on
peut trouver une base de
. La matrice est diagonalisable lorsqu'on
peut trouver une base de
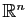 constituée de vecteurs appartenant aux sous-espaces propres. La
matrice de passage
constituée de vecteurs appartenant aux sous-espaces propres. La
matrice de passage 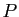 est la matrice exprimant ces vecteurs dans la base
canonique. Quelques exemples élémentaires sont donnés dans les
exercices 10 et 11.
est la matrice exprimant ces vecteurs dans la base
canonique. Quelques exemples élémentaires sont donnés dans les
exercices 10 et 11.
Quand une matrice 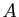 est diagonalisable, il est facile de résoudre
le système linéaire
est diagonalisable, il est facile de résoudre
le système linéaire 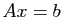 : il est équivalent au système
: il est équivalent au système
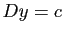 , avec
, avec 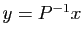 et
et 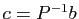 . Or dans un système dont la
matrice est diagonale, toutes les équations n'ont qu'une inconnue et
se résolvent séparément.
. Or dans un système dont la
matrice est diagonale, toutes les équations n'ont qu'une inconnue et
se résolvent séparément.
Prenons maintenant l'exemple
d'un système d'équations de récurrence linéaire,
du type
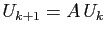 , où
, où  désigne un vecteur dont on
souhaite connaître l'expression en fonction de
désigne un vecteur dont on
souhaite connaître l'expression en fonction de 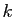 . Du point de
vue théorique, il n'y a pas de problème :
. Du point de
vue théorique, il n'y a pas de problème :
Mais cela n'avance à rien si on ne sait pas calculer formellement
l'expression de 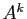 en fonction de
en fonction de 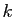 . C'est possible si
. C'est possible si 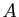 est
diagonalisable. En effet, si
est
diagonalisable. En effet, si
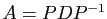 :
:
Ecrire 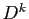 est immédiat. On en déduit l'expression
générale de
est immédiat. On en déduit l'expression
générale de 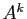 , donc de
, donc de  . Dans l'exemple ci-dessus, on
trouve :
. Dans l'exemple ci-dessus, on
trouve :
Passons maintenant aux systèmes d'équations différentielles, du type
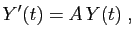 |
(1) |
où 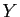 est une fonction (inconnue) de
est une fonction (inconnue) de
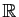 dans
dans
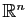 , et
, et
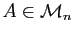 est une matrice carrée de réels.
Si
est une matrice carrée de réels.
Si
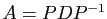 , alors
, alors
Donc
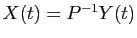 est solution du système
est solution du système
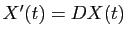 . En
posant
. En
posant
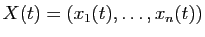 , ce système s'écrit
, ce système s'écrit
Sa solution est facile à calculer :
Le vecteur des conditions initiales pour le système
diagonalisé est
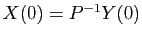 . Connaissant
. Connaissant 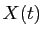 , on en
déduit
, on en
déduit
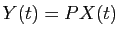 .
Soit par exemple à résoudre
.
Soit par exemple à résoudre
avec les conditions initiales 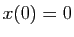 ,
, 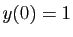 ,
, 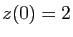 .
Le système s'écrit sous la forme
.
Le système s'écrit sous la forme
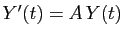 , avec
, avec
En utilisant la diagonalisation de 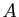 , on obtient
, on obtient
Présentée ainsi la diagonalisation semble un outil magique. En
réalité, les algorithmes qui calculent numériquement les valeurs
propres et les vecteurs propres sont relativement lents et il est impossible
de diagonaliser une matrice si sa dimension dépasse quelques dizaines.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![\begin{displaymath}
(a)
\left\{
\begin{array}{rrrcr}
&y&+z&=&1 \ [2ex]
-\frac{1...
...x&&&=&0 \ [2ex]
&-y&&=&-1\ [2ex]
&&2z&=&0
\end{array}\right.
\end{displaymath}](img462.gif)
![\begin{displaymath}
(a)
\left\{
\begin{array}{rrrcr}
&y&+z&=&1 \ [2ex]
-\frac{1...
...x&&&=&0 \ [2ex]
&-y&&=&-1\ [2ex]
&&2z&=&0
\end{array}\right.
\end{displaymath}](img462.gif)
![\begin{displaymath}
(a)
\left\{
\begin{array}{lcrrr}
u_{k+1} &=&&v_k&+w_k \ [2e...
...
v_{k+1}&=& &-v_k&\ [2ex]
w_{k+1}&=&&&2w_k
\end{array}\right.
\end{displaymath}](img463.gif)
![\begin{displaymath}
(a)
\left\{
\begin{array}{lcrrr}
x'(t) &=&&y(t)&+z(t) \ [2e...
...x]
y'(t)&=& &-y(t)&\ [2ex]
z'(t)&=&&&2z(t)
\end{array}\right.
\end{displaymath}](img464.gif)
![\begin{displaymath}
A=
\left(
\begin{array}{rrr}
0&1&1\ [2ex]
-\frac{1}{2}&\fra...
...r}
1&0& 0\ [2ex]
0&-1& 0\ [2ex]
0&0& 2
\end{array}\right)
\end{displaymath}](img465.gif)
![]() et
et ![]() sont
semblables, c'est-à-dire qu'elles représentent
le même endomorphisme dans deux bases
différentes, ou encore, il existe une matrice de passage
sont
semblables, c'est-à-dire qu'elles représentent
le même endomorphisme dans deux bases
différentes, ou encore, il existe une matrice de passage ![]() telle que
telle que
![]() .
.
![\begin{displaymath}
\stackrel{
\underbrace{
\left(
\begin{array}{rrr}
\frac{1}{2...
...& 0\ [2ex]
0&-1& 0\ [2ex]
0&0& 2
\end{array}\right)
}}{D}
\end{displaymath}](img468.gif)
![]() est diagonalisable, il est facile de résoudre
le système linéaire
est diagonalisable, il est facile de résoudre
le système linéaire ![]() : il est équivalent au système
: il est équivalent au système
![]() , avec
, avec ![]() et
et ![]() . Or dans un système dont la
matrice est diagonale, toutes les équations n'ont qu'une inconnue et
se résolvent séparément.
. Or dans un système dont la
matrice est diagonale, toutes les équations n'ont qu'une inconnue et
se résolvent séparément.
![]() , où
, où ![]() désigne un vecteur dont on
souhaite connaître l'expression en fonction de
désigne un vecteur dont on
souhaite connaître l'expression en fonction de ![]() . Du point de
vue théorique, il n'y a pas de problème :
. Du point de
vue théorique, il n'y a pas de problème :
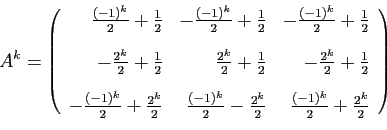
![\begin{displaymath}
\left\{
\begin{array}{lcrrr}
x'(t) &=&&y(t)&+z(t) \ [2ex]
y...
...}x(t)&-\frac{3}{2}y(t)&+\frac{1}{2} z(t)
\end{array}\right.\;,
\end{displaymath}](img493.gif)
![\begin{displaymath}
Y(t) =
\left(
\begin{array}{r}
x(t)\ [2ex]
y(t)\ [2ex]
z(...
...ex]
\frac{3}{2}&-\frac{3}{2}&\frac{1}{2}
\end{array}\right)\;.
\end{displaymath}](img498.gif)
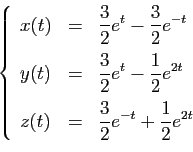
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales