Les avocats de Cambridge

Tous deux ont fait leurs études à Cambridge, tous deux ont exercé assez longuement comme avocats tout en considérant cela comme un moyen accessoire de gagner leur vie, tous deux ont fini professeurs de mathématiques. Ils étaient amis, et se sont influencés l'un l'autre par leurs travaux respectifs, même s'il n'ont cosigné aucun article¹. Nous parlons de Arthur Cayley (1821-1895) et de James Joseph Sylvester (1814-1897). Voici ce que disait le second, vers la fin de sa carrière.

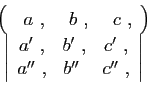
Cayley, who, though younger than myself is my spiritual progenitor - who first opened my eyes and purged them of dross so that they could see and accept the higher mysteries of our common mathematical faith...

Sylvester est le premier qui a employé le mot «matrix» en 1850. L'année suivante, il explicite l'analogie qui l'a conduit à ce terme.

I have in a previous paper defined a ``Matrix'' as a rectangular array of terms, out of which different systems of determinants may be engendered, as from the womb of a common parent.

Au début, une matrice n'était donc qu'un tableau à partir duquel étaient engendrés des déterminants. C'est Cayley qui a le premier en 1858 traité les matrices comme de nouveaux objets mathématiques, susceptibles d'être ajoutés et multipliés. Lisez le début de «A memoir on the Theory of Matrices», et admirez l'élégance et la concision du style (les notations ont légèrement changé).

The term matrix might be used in a more general sense, but in the present memoir I consider only square and rectangular matrices, and the term matrix used without qualification is to be understood as meaning a square matric; in this restricted sense, a set of quantities arrranged in the form of a square, e. g.

$$\begin{array}{c} \left(\begin{array}{ccc}\; a ,&\; b ,&\;\... ...' ,&c' ,\ a'' ,&b'' &c'' ,\end {array}\right\vert \end{array}$$

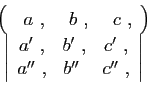
is said to be a matrix.

[...]

It will be seen that matrices (attending only to those of the same order) comport themselves as single quantities; they may be added, multiplied or compounded together, &c. : the law of addition of matrices is precisely similar to that for the addition of ardinary algebraix quantities; as regards their multiplication (or composition), there is the peculiarity that matrices are not in general convertible; it is nevertheless possible to form the powers (positive or negative, integral or fractional) of a matrix, and thence to arrrive at the notion of a rational and intergal function, or generally os any algebraical function, of a matrix.

Le style de Sylvester était moins dépouillé que celui de Cayley. Ils se rejoignaient pourtant dans leurs opinions esthétiques.

Cayley :

«As for everything else, so for a mathematical theory: beauty can be perceived but not explained.

Sylvester :

«May not music be described as the mathematics of the sense, mathematics as music of the reason? The musician feels mathematics, the mathematician thinks music: music the dream, mathematics the working life.