La méthode du pivot de Gauss n'est
pas exactement programmée comme elle a été présentée. Il
y a plusieurs raisons à cela, dont la principale est le problème
de la précision numérique.
Voici un système de deux équations
à deux inconnues, dépendant du paramètre
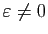 .
.
Voici le même système, après avoir échangé les deux
équations.
Les deux solutions sont évidemment les mêmes. Pourtant, si
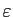 est très petit en valeur absolue,
les deux calculs ne sont pas du tout équivalents
numériquement : diviser par un petit nombre, ou
multiplier par un grand nombre,
augmente les erreurs d'approximation.
Telles que nous les avons présentées, les permutations de lignes et de
colonnes servent à assurer que les pivots restent non nuls.
La plupart des systèmes que l'on rencontre en pratique ont une
solution unique : ce sont des systèmes de
est très petit en valeur absolue,
les deux calculs ne sont pas du tout équivalents
numériquement : diviser par un petit nombre, ou
multiplier par un grand nombre,
augmente les erreurs d'approximation.
Telles que nous les avons présentées, les permutations de lignes et de
colonnes servent à assurer que les pivots restent non nuls.
La plupart des systèmes que l'on rencontre en pratique ont une
solution unique : ce sont des systèmes de 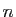 équations à
équations à 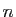 inconnues, de rang
inconnues, de rang 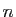 . En général, on peut leur appliquer la
méthode du pivot de Gauss sans rencontrer de pivot nul. Mais on
utilise quand même les permutations de lignes et de colonnes,
pour faire en sorte qu'à chaque étape,
le pivot soit le plus grand
possible en valeur absolue.
. En général, on peut leur appliquer la
méthode du pivot de Gauss sans rencontrer de pivot nul. Mais on
utilise quand même les permutations de lignes et de colonnes,
pour faire en sorte qu'à chaque étape,
le pivot soit le plus grand
possible en valeur absolue.
Permuter les lignes d'une matrice, revient à la multiplier
à gauche par une matrice de
permutation. Une matrice de permutation est la matrice de passage de
la base
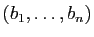 à la base
à la base
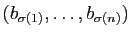 , où
, où 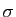 est une
bijection de
est une
bijection de
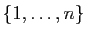 dans lui-même.
Ses coefficients
d'ordre
dans lui-même.
Ses coefficients
d'ordre
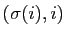 valent 1, les autres 0.
Permuter les colonnes d'une matrice, revient à la multiplier
à droite par une autre matrice de
permutation. En permutant les lignes et les colonnes, on remplace la
matrice
valent 1, les autres 0.
Permuter les colonnes d'une matrice, revient à la multiplier
à droite par une autre matrice de
permutation. En permutant les lignes et les colonnes, on remplace la
matrice 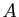 par la matrice
par la matrice 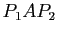 où
où 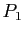 et
et 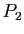 sont deux
matrices de permutation.
sont deux
matrices de permutation.
Dans sa version la plus courante, l'algorithme ne considère que des
permutations de lignes : il remplace donc la matrice 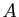 par
par 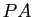 ,
où
,
où 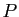 est une matrice de permutation.
Une fois choisi l'ordre dans lequel on traite les
lignes, la
est une matrice de permutation.
Une fois choisi l'ordre dans lequel on traite les
lignes, la 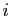 -ième étape de la méthode consiste à ajouter aux
lignes d'indice
-ième étape de la méthode consiste à ajouter aux
lignes d'indice
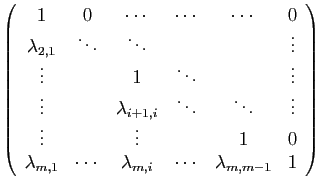
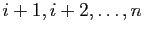 la
la 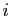 -ième ligne multipliée par
un certain coefficient. Cela revient à multiplier à gauche par une
matrice du type suivant.
-ième ligne multipliée par
un certain coefficient. Cela revient à multiplier à gauche par une
matrice du type suivant.
Le produit de ces matrices, pour 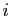 allant de
allant de 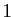 à
à 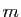 est la
matrice ci-dessous.
est la
matrice ci-dessous.
Son inverse est encore une matrice du même type : trianglaire
inférieure avec des 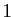 sur la diagonale. On la note
sur la diagonale. On la note 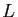 (pour
«lower triangular»). Le produit
(pour
«lower triangular»). Le produit 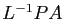 est une matrice
triangulaire supérieure, que l'on note
est une matrice
triangulaire supérieure, que l'on note 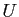 pour «upper
triangular» :
pour «upper
triangular» : 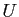 est la forme échelonnée de
est la forme échelonnée de 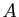 .
.
La décomposition LU de la matrice 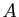 est la donnée des trois
matrices
est la donnée des trois
matrices 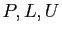 telles que
telles que 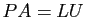 .
Si on doit résoudre le système
.
Si on doit résoudre le système 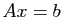 , on le transformera en deux
systèmes triangulaires, un de matrice
, on le transformera en deux
systèmes triangulaires, un de matrice 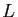 , l'autre de matrice
, l'autre de matrice 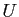 .
.
Il arrive fréquemment que l'on ait à résoudre
successivement de nombreux systèmes linaires ayant tous la même
matrice 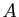 , mais des seconds membres différents. Calculer au
préalable la décomposition LU de
, mais des seconds membres différents. Calculer au
préalable la décomposition LU de 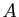 réduit de beaucoup
le temps de calcul. Pour certaines matrices qui reviennent
souvent dans les calculs, la décomposition LU figure dans les
bibliothèques de codes, et elle est
chargée en mémoire avant le début du calcul.
réduit de beaucoup
le temps de calcul. Pour certaines matrices qui reviennent
souvent dans les calculs, la décomposition LU figure dans les
bibliothèques de codes, et elle est
chargée en mémoire avant le début du calcul.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() .
.
![$\displaystyle \left\{\begin{array}{rcl}
\varepsilon x+y&=&1\ [2ex]
x+y&=&2
\en...
...]
y&=&(2-\frac{1}{\varepsilon })/(1-\frac{1}{\varepsilon })
\end{array}\right.
$](img501.gif)
![$\displaystyle \left\{\begin{array}{rcl}
x+y&=&2\ [2ex]
\varepsilon x+y&=&1
\en...
...varepsilon )\ [2ex]
y&=&(1-2\varepsilon )/(1-\varepsilon )
\end{array}\right.
$](img502.gif)
![]() à la base
à la base
![]() , où
, où ![]() est une
bijection de
est une
bijection de
![]() dans lui-même.
Ses coefficients
d'ordre
dans lui-même.
Ses coefficients
d'ordre
![]() valent 1, les autres 0.
Permuter les colonnes d'une matrice, revient à la multiplier
à droite par une autre matrice de
permutation. En permutant les lignes et les colonnes, on remplace la
matrice
valent 1, les autres 0.
Permuter les colonnes d'une matrice, revient à la multiplier
à droite par une autre matrice de
permutation. En permutant les lignes et les colonnes, on remplace la
matrice ![]() par la matrice
par la matrice ![]() où
où ![]() et
et ![]() sont deux
matrices de permutation.
sont deux
matrices de permutation.
![]() par
par ![]() ,
où
,
où ![]() est une matrice de permutation.
Une fois choisi l'ordre dans lequel on traite les
lignes, la
est une matrice de permutation.
Une fois choisi l'ordre dans lequel on traite les
lignes, la ![]() -ième étape de la méthode consiste à ajouter aux
lignes d'indice
-ième étape de la méthode consiste à ajouter aux
lignes d'indice
![]() la
la ![]() -ième ligne multipliée par
un certain coefficient. Cela revient à multiplier à gauche par une
matrice du type suivant.
-ième ligne multipliée par
un certain coefficient. Cela revient à multiplier à gauche par une
matrice du type suivant.

![$\displaystyle Ax=b \Longleftrightarrow PAx=Pb
\Longleftrightarrow LUx=Pb
\Longleftrightarrow
\left\{\begin{array}{l}
Ly=Pb\ [2ex]
Ux=y
\end{array}\right.
$](img521.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales