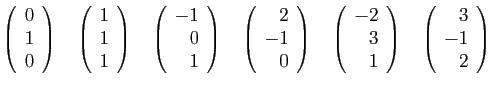
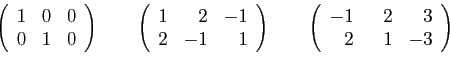
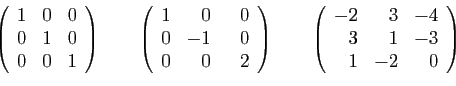
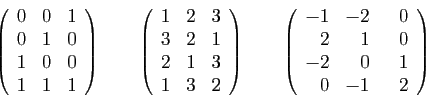
- Ecrire la transposée de chacune de ces matrices.
- Etant données deux matrices
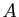 ,
, 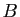 appartenant à l'ensemble ci-dessus, calculer ceux des produits
appartenant à l'ensemble ci-dessus, calculer ceux des produits
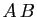 ,
,
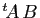 ,
,
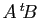 ,
,
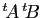 qui sont définis.
qui sont définis.
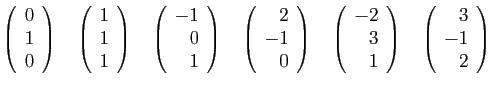
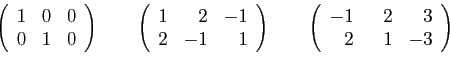
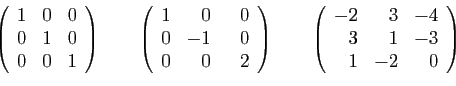
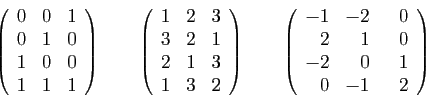
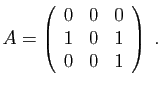
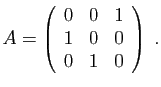
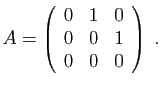
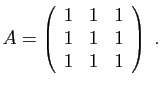
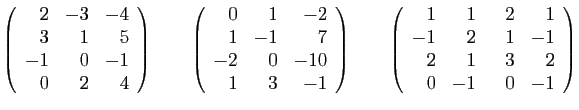
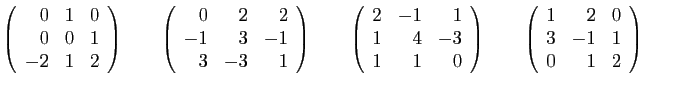
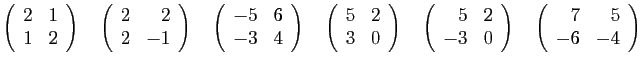
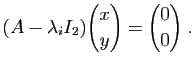
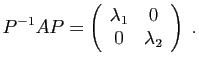
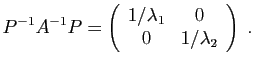
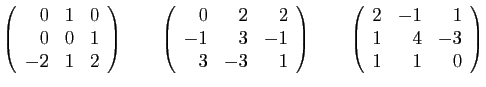
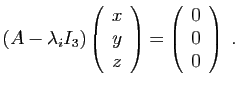
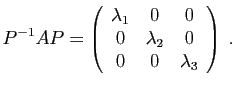
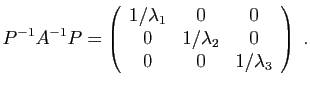
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales