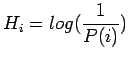
Le codage sans perte permet de comprimer des données: documents texte, tableurs, fichiers exécutables, etc. ; il fait souvent partie intégrante de l'encodage des données lors des transmissions réseau. Parmi les plus connues de ces méthodes figurent le codage RLE, le codage de HUFFMAN ou bien encore le codage LZW.
Un codeur non-adaptatif est fait pour coder un certain type de données. Par exemple, on peut concevoir un codeur pour compresser spécifiquement la langue française; il contiendra notamment les mots ("de", "en", "avec", ...) qui apparaissent fréquemment pour leur assurer un codage optimal.
À l'inverse, un codeur adaptatif n'intègre aucune donnée statistique concernant les données. La dépendance des données s'effectue à la volée. C'est pourquoi on parle aussi de codage dynamique. Un exemple (HUFFMAN dynamique) sera présenté dans la prochaine section. Ce type de codage s'adapte au type de données en entrée et fournit un taux de compression "le meilleur possible".
Il existe également des codeurs dits semi-adaptatifs qui sont un mélange de ces deux méthodes: un premier passage sur les données permet de construire un dictionnaire, un second effectue l'encodage. Ainsi, un dictionnaire optimal est construit avant encodage.
L'entropie d'une source est la quantité moyenne d'information contenue dans cette source. Cette mesure a été introduite par Shannon. En pratique, elle représente une mesure de l'incertitude liée à la probabilité d'occurrence des événements. Pour la calculer, on définit la quantité d'information:
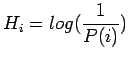
La source produit en moyenne une quantité d'information égale à la somme des espérances des quantités d'information; cette quantité est notée H et est nommée entropie:
![$\displaystyle H=\sum_i{E[H_i]}=\sum_i H_i P(i)$](img2.png)
On montre que le nombre de bits moyen nécessaire pour coder un symbole d'un message est toujours supérieur à l'entropie de ce message.
Cette quantité est maximale lorsque tous les événements (symboles émis par la source) sont équiprobables. Plus l'entropie est élevée, plus la compression est difficile (mais parfois efficace en utilisant une organisation différente de l'information; on parle alors de compression logique).
L'algorithme RLE (Run-Length Encoding) est un algorithme extrêmement simple permettant de diminuer l'entropie de données. Le principe consiste à détecter les répétitions et à les encoder différemment. En pratique, une chaîne répétée est encodée sur deux octets: le premier annonce le nombre de répétitions; le second indique le caractère à répéter.
Par exemple, la chaîne "aaaaaaaa" peut être codée "8a".
Le problème est bien évidemment qu'un fichier ne contenant aucune répétition aura une taille deux fois plus importante que l'original! En pratique, on encode les répétitions sur trois caractères: le premier est un caractère spécial indiquant la présence d'une répétition; le second indique le nombre d'occurences et le troisième la valeur à répéter.
Ainsi la chaîne "aiiiiiibcddddde" sera encodée, avec pour caractère spéciale le signe dièse #: "a#6ibc#5de", ce qui représente une compression de 33,3% .
Le codage RLE est notamment employé dans les formats d'image PCX ou BMP, ou bien avant un autre algorithme de compression (notamment HUFFMAN dans le cas de JPEG).